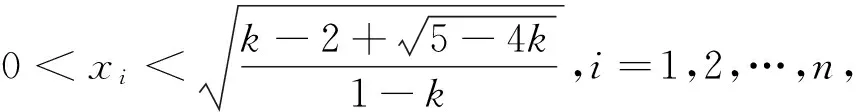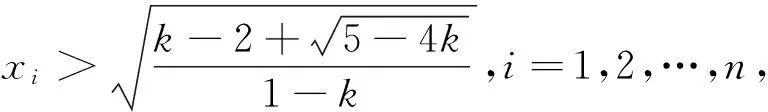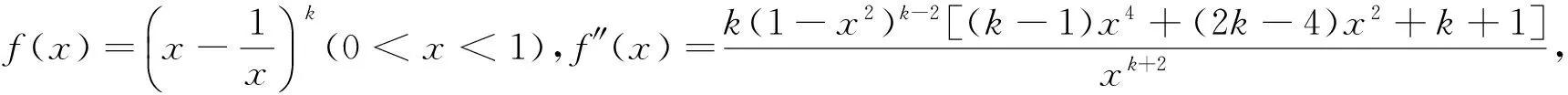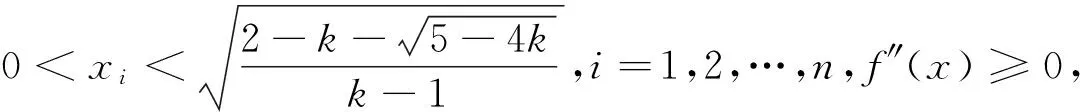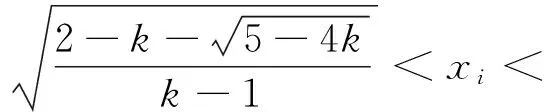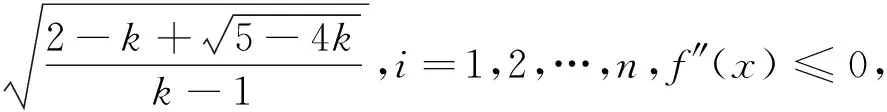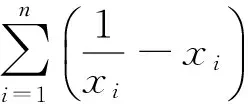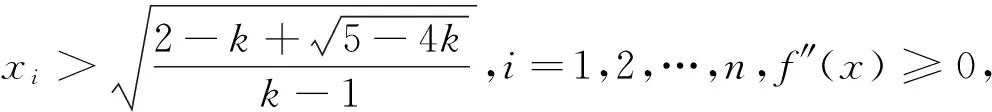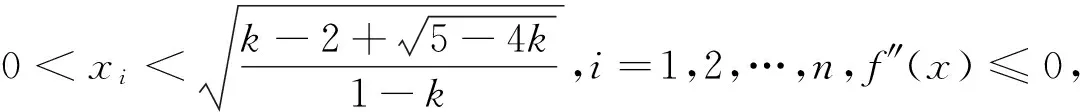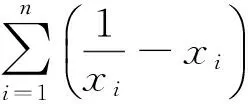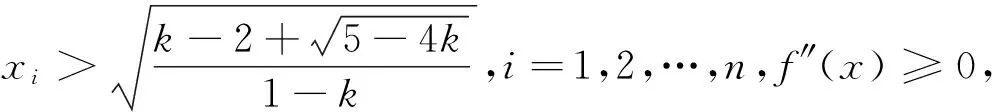一个不等式的简证及猜想的推广

浙江省德清县第三中学 (313201) 王 丹浙江大学附属中学丁兰校区 (310021) 施刚良

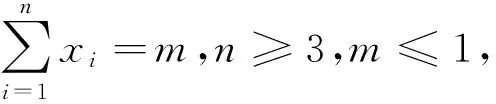
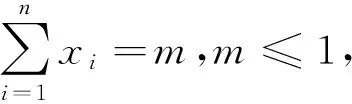
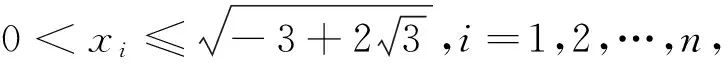
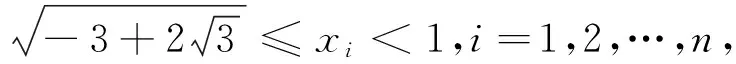
在给出引理的简证及命题1、命题2之前，笔者先给出有关下凸函数的两个性质：

1.若函数y=f(x)在定义域D上二阶可导，则y=f(x)在D上为下凸函数的充分必要条件是f″(x)≥0.

2.若函数y=f(x)在定义域D上是下凸函数，则对∀x1,x2,…,xn∈D，都有

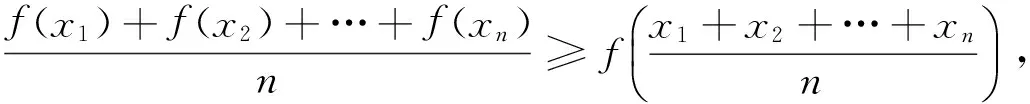
注：上凸函数的性质与下凸函数的性质是对立的，在此笔者就不再叙述了.

下面先给出引理的简证：

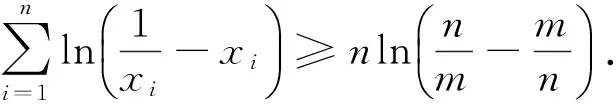
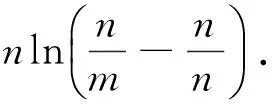
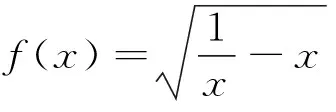
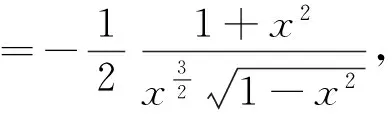
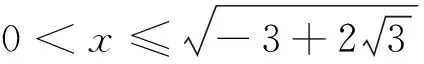
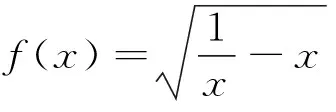
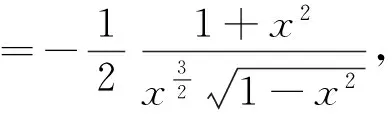
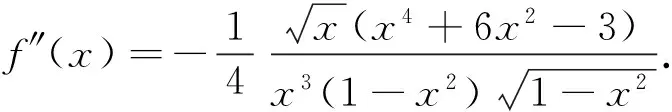
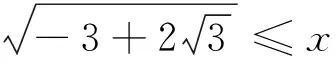
著名数学家波利亚说过：没有任何一个题目是彻底完成了的，总还会有些事情可以做；在经过充分的研究和观察以后，我们可以将任何解题方法加以改进；而且无论如何，我们总可以深化我们对答案的理解.笔者通过进一步探究发现还可以将上述命题再推广：

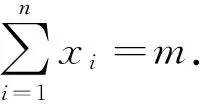
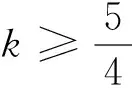
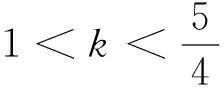
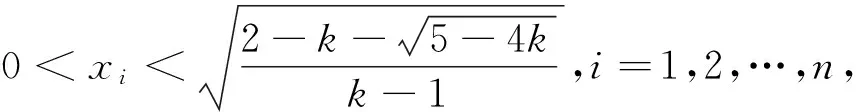
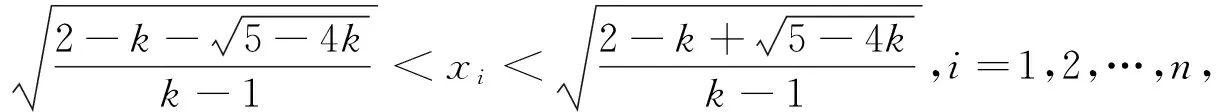
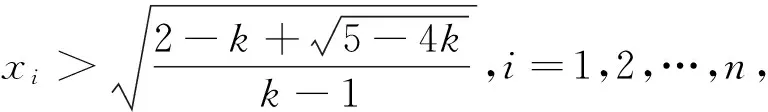
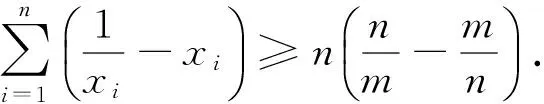
(4)当0

证明：(3)当k=1时，由引理知

(4)当0

[1]周斌.一个不等式猜想的证明及推广[J].中学数学研究(广东)，2010(2)：48.