基于气动热约束的高超声速电缆罩封头外形优化设计

刘芙群，孙晓峰，杨鸿俊，涂建秋



基于气动热约束的高超声速电缆罩封头外形优化设计

刘芙群，孙晓峰，杨鸿俊，涂建秋

（中国运载火箭技术研究院，北京，100076）

基于N-S方程数值计算方法对高超声速气流中导弹电缆罩封头和其后方的电缆罩外形进行气动热计算，对2种封头外形的气动热进行对比分析，研究了其流动机理和流场结构。结果表明：优化后的与后方电缆罩等宽、等高的封头外形极大地降低了电缆罩的热环境。

气动热；高超声速；电缆罩封头；外形优化

0 引 言

高超声速流流过流场中的突起物时，在突起物上游形成弓形脱体激波，脱体激波引起的逆压梯度通过边界层内的亚声速区向激波上游传播，从而引起弹体上的边界层分离，在分离区内形成一些漩涡，引起局部流场中的激波和边界层干扰，这些干扰流场特性使突起物附近的压力与热流显著增大，在设计不当的情况下，会造成严重后果[1]。

在导弹总体布局设计中，为了连接飞行器内的电气系统，需要使用跨越多个舱段的穿舱电缆，电缆一般紧贴发动机等部段的外壁安装，飞行过程中电缆要受到外部气动力、热载荷作用。为确保电缆在飞行中的可靠工作，一般在电缆外设置有电缆罩，为了保护电缆罩，在电缆罩前设计有封头。电缆罩及其封头的安装位置和结构特点决定其成为典型的高超声速流场中的突起物。电缆罩封头作为保护电缆罩本体的关键结构，其外形的优化与否不仅决定自身的工作可靠性，如果设计不当，还会对后面的电缆罩的热环境产生较大的干扰，影响其气动热环境。因此，设计中必须对电缆罩封头外形进行优化设计。

电缆罩及其封头的特征高度一般和高雷诺数气流边界层厚度同量级，属于微型局部突起物[2]，其热环境以及对周围结构的干扰和以往已经研究较多的弹上的翼、舵等较高的突起物不同。过去几十年来，已有很多文献对突起物附近的干扰流场进行了定性的描述，但是研究结果只局限于可归结某类规则外形突起物，迄今为止有关特殊的非规则外形突起物的气动热环境研究的相关文献还相对较少。由于电缆进出口以及弹体结构的设计要求，电缆罩封头以及电缆罩很难将其设计成规则的圆柱、方柱、压缩拐角等规则外形。因而用以试验数据为基础的工程算法估算其热环境就不现实了，因此采用数值计算和测热试验来确定其干扰热环境非常必要[3]。

本文基于N-S方程, 采用有限体积法，对电缆罩封头和其干扰下的电缆罩热环境进行了数值计算，对流场结构和流动机理进行了分析，提出并验证了降低电缆罩热环境的新的封头外形。

1 计算模型

为了分析气动热的三维效应，计算时考虑了全弹外形，弹身外形均为双锥+柱。计算了2种外形的电缆罩封头外形，如图1和图2所示。2种外形的电缆罩封头和电缆罩位于弹体的相同部位，电缆罩封头位于弹体第二锥上，电缆罩本体位于弹体柱段上，整个电缆罩周向位于弹体的Ⅱ、Ⅳ象限线上。弹体和电缆罩外形示意见图3。2种外形封头的高度相同，长度相同。为保护后面的电缆罩防热结构，第1种封头比后面的电缆罩高5.5 mm、宽35 mm。第2种封头高度、宽度与后方电缆罩相同。

计算条件为马赫数5.7，高16.8 km，湍流状态，壁面温度273 K。

图1 封头外形1示意

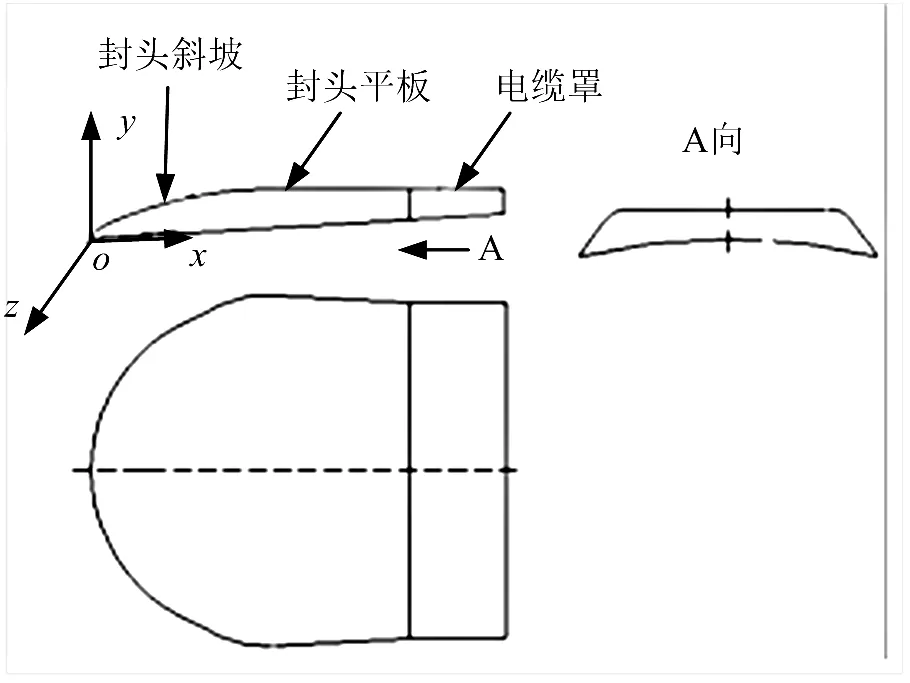
图2 封头外形2示意

图3 全弹示意

2 数值计算方法

2.1 控制方程

控制方程为三维非定常可压缩N-S方程，采用有限体积法进行求解，基本方程为

式中为守恒变量；，分别为，，3个方向上的无粘通量矢量；v，v，v分别为，，3个方向上的粘性通量矢量；具体形式可参见文献[4]和文献[5]。

2.2 空间离散格式

空间离散格式对于流场的计算精度和稳定性均有较大影响，本文采用ROE的FDS格式进行界面无粘数值通量的计算。

计算过程中引入熵修正，将非物理的膨胀激波耗散为膨胀扇区，使之满足熵条件。M. J. Kermani and E.G. Plett的熵修正格式：

2.3 湍流模型

由于飞行雷诺数较高，层流假设不再适用，因此本文采用Spalart-Allmaras单方程湍流模型对湍流进行模拟，具体形式可参见文献[4]。

3 网格生成

本文采用了目前广泛使用的分区对接结构网格技术，它的基本思想是：首先将总体区域分成若干个子区域，再对每个子区域分别建立网格，并在每个网格上对方程分别求解，各子区域的解在内边界的传递则通过插值来实现[4]。区域分解的基本原则是：尽量使每个子域的边界简单，以便于建立结构网格；各子区域大小也尽量接近，以实现计算负载的平衡。为了保证所生成的网格具有很高的质量，网格生成时遵循了以下基本要求：

a）网格在空间具有良好的正交性；

b）网格光滑过渡，相邻网格尺寸不相差过大，以减小计算误差，保证流场计算的精度；

c）尽量减少分区的数目，在流动复杂的区域尽量生成单块网格；

d）网格有合理的分布，要能反映流场特征。在流动梯度大的地方，如激波附近、边界层内布置密集的网格；而在流动梯度小的地方，如远场附近网格稀疏一些，以减少计算量[4~6]。

4 计算结果分析

4.1 热流密度

图4和图5给出了封头外形1和封头外形2中心线处的无量纲热流曲线。选用的参考热流为封头上游35倍于电缆罩封头高度处的弹壁上的热流。横坐标为封头位置坐标用封头高度无量纲化后的距离，坐标系的定义见图2和图3。

图4 外形1的中心线处的无量纲热流分布

图5 外形2中心线处的无量纲热流曲线分布

从图4和图5可以看出，因为2个封头的高度一致，均在边界层内，封头斜坡的后掠角基本一致，因此封头中心线上的热流基本相当，对封头前弹壁的干扰也基本相当。封头斜坡迎风面上的热流存在较大的峰值，基本为远前方无干扰处的14倍左右，这是高速边界层气流冲击的结果。分离距离在0.7倍的封头高度左右，越靠近封头，弹壁的热流越高，最高值为远前方无干扰处的5.5倍左右。封头平板处的热流稍大于远前方无干扰处的热流。

图6至图9分别给出了2个外形的电缆罩侧面和顶面上的无量纲热流分布，电缆罩顶面和侧面热流线定义见图10至图13。

参考点选取距离电缆罩下游14倍于电缆罩高度处的电缆罩上未受干扰的热流和压力。向坐标原点位于电缆罩起始位置，顺着来流方向为正。

图6 外形1电缆罩顶面上的无量纲热流分布

图7 外形1电缆罩侧面上的无量纲热流分布

图8 外形2电缆罩顶面上的无量纲热流分布

图9 外形2电缆罩侧面上的无量纲热流分布

图10 外形1顶面热流参考线

图11 外形1侧面热流参考线

图12 外形2顶面热流参考线

图13 外形2侧面热流参考线

由图6至图13可见，外形1电缆罩顶面和侧面的热流峰值明显高于外形2，且侧面热流峰值达到了基准值的17倍左右，外形1的侧面峰值热流是外形2的4倍和3倍左右，且外形1的热流随着向距离增加呈现先增加后减小的规律，外形2的热流随着向距离增加呈现单调减小的规律。

由以上分析可见，经过优化设计后，消除了高度差和宽度差的封头外形2，极大地改善了封头后的电缆罩热环境，其自身热环境的分布、大小和原外形差异较小。

4.2 流场分析

图14和图15给出了2个外形的流线和压力系数。

图14 外形1的压力系数和流线

图15 外形2的压力系数和流线

从图14和图15可以看出：

a）2个外形下，电缆罩前封头表现了高超声速绕突起物的流动特征：来流在前封头处受到压缩，使得前封头斜坡处压力增大，呈现高压区，前封头前方弹身上由分离激波导致，也存在高压区，2个外形所产生的高压区并无大的差异，这和文献[1]和文献[7]的结论是一致的。

b）2个外形在电缆罩处的流动上存在明显差异：外形1的电缆罩最前端压力相对较小，这是由于前封头平板与电缆罩之间存在高度差和宽度差使得气流在此处发生膨胀，压力减小，为局部低压区；从壁面流线可以看出，气流经过前封头台阶后，膨胀造成的局部低压和外侧的高压使气流分离，在电缆罩的前端出现回流，明显偏向电缆罩，流动情况较为复杂。气流过度膨胀到达电缆罩壁面，由于此处需要一道激波来调整气流的参数，故形成了过膨胀压缩激波，使得在电缆罩低压区后的区域压力增大，产生分离再附[8]。另外，高度差和宽度差都可能引起过膨胀压缩激波。电缆罩和封头的高度差和宽度差均引起了过膨胀压缩激波，由于宽度差比高度差大，故侧面产生的过膨胀压缩激波更强，使电缆罩侧面产生较为严重的气动加热。

对于外形2，由于封头平板的宽度和高度和电缆罩的相同，气流经过封头处的压缩、封头平板处的膨胀后，在电缆罩前端并未出现明显的分离现象，因此其气动加热显著低于外形1。

5 结 论

本文对2种外形的电缆罩封头进行了气动热数值计算，对流场结构、对流动机理进行了研究，对封头自身的热环境、弹壁的干扰热环境以及封头后的电缆罩的热环境进行了对比分析，结果表明：

a）本文使用的数值计算方法可用于高度和边界层厚度同等量级的微小突起物的气动热计算和分析；

b）高速气流对突起物前缘斜坡的冲击较大，导致其热流较高；

c）对于后掠角和高度相同的斜坡形突起物，其热环境分布和峰值均相差较小；

d）对于弹上有较大宽度差和高度差的前后连接突起物，宽度差和高度差会引起较强烈的过膨胀压缩激波和分离再附问题，导致后面突起物的热环境数值激大；

e）优化设计后的封头自身热环境和原外形相似，但能极大地改善封头后的电缆罩体热环境，达到了外形优化设计的目的。

[1] 李素循. 激波与边界层主导的复杂流动[M]. 北京: 科学出版社, 2007.

[2] 耿湘人, 桂业伟, 王安龄. 微型突起物高超声速气动热特性研究[J]. 空气动力学学报, 2006, 24(2): 266-268.

[3] Greene, Francls A B, Gregory M W, William A. Measured and computed hyp-ersonic aerodynamic/aeroheating characteristics for an elliptically blunted flared cylinder[C]. Reno: 39th Aerospace Sciences Meeting and Exhibit, 2001.

[4] 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2007.

[5] 阎超, 禹建军, 李君哲. 热流CFD计算中格式和网格效应若干问题研究[J]. 空气动力学学报, 2006, 24(1): 125-130.

[6] Stephen J A. A structured-grid quality measure for simulated hypersonic flows[C]. Reno: 42nd AIAA Aerospace Sciences Meeting and Exhibit, 2004.

[7] 潘宏禄, 马汉东, 王强. 压缩拐角激波/湍流边界层干扰特性分析[J]. 计算物理, 2008, 25(5): 549-554.

[8] 范绪箕, 董葳. 飞行器突起物周围气动加热的计算方法[J]. 宇航学报, 1998, 19(1): 98-102.

Optimization of Cable Fairing Former Structure Submitted to Aerodynamic Thermal Constraints in Hypersonic Flows

Liu Fu-qun, Sun Xiao-feng, Yang Hong-jun, Tu Jian-qiu

（China Academy of Launch Vehicle Technology, Beijing, 100076)

The hypersonic flow around the former structure of cable fairing is numerically simulated based on Navier-Stokes equation. Aeroheating fluxes comparison between two cable fairings is made. Flow field structure and flow mechanics is analysed. It is found that the aerodynamic heating of optimized design is greatly reduced than the original cable fairing, whose height and width are the same as the former structure in it.

Aerodynamic heating; Hypersonic; Cable fairing; Optimization design

1004-7182(2017)06-0007-05

10.7654/j.issn.1004-7182.20170602

V411

A

2015-12-07；

2017-10-16

刘芙群（1972-），女，研究员，主要研究方向为飞行器气动力和热环境