复杂内凹型囊体结构非线性解法仿真预示

张 妍



复杂内凹型囊体结构非线性解法仿真预示

张 妍

（中国运载火箭技术研究院研究发展中心，北京，100076）

由于膜结构的大位移、大变形等非线性特性，气膜的承压仿真是一个复杂的数值过程，若考虑气膜外壁与支撑结构之间的接触、气膜的限位约束对流体的作用等一系列问题，将会增加充气结构承压计算过程的复杂性，很难找到适用的理论解析解对其进行有效的解答。采用非线性显式求解方法解决了气膜结构涉及的膜单元的甄选、几何非线性以及接触引起的离散求解过程的稳定性问题，为此类气膜结构的承压计算问题提供合理适用的计算方法。

气膜结构；数值仿真；承压

0 引 言

囊体结构是一种张力体结构[1]，是由弹性薄膜材料通过充压使其囊体内部产生一定的预张应力以维持特定空间形状，并且能承受一定的外部载荷的作用。在火箭发射时，囊体结构可内部残留少许气体折叠放置在火箭发射舱里，不占用额外的发射空间；发射入轨后，囊体结构在其内部气压的作用下膨胀展开，可释放作为空间靶标使用，也可作为航天结构配件。由于囊体结构膨胀后体积大、弹性好，具有较强的缓冲性能，且由于成本低、质量轻等优点使囊体结构得到广泛的应用。因此研究充气膜结构的力学性能，掌握膜结构的数值仿真方法对提高中国深空领域探测技术能力具有重要的指导意义[2]。

Fushou Liu对扁豆状的两面膜的动力学特性进行了数值模拟，建立了动力学方程，并给出膜的基频表达方式[3]。但此种方法运算复杂、计算量大，且对于复杂外形的膜片很难给出其动力学方程表达式。朱利君[4]对飞艇类的充气膜结构进行了详细的研究，采用Abaqus中分析步step对载荷的施加以及计算过程进行控制。但计算模型过于简单，囊体膜单元仿真计算时出现了“褶皱”现象。

由于此类膜单元计算时会遇到大位移大变形等非线性问题，再加上接触等非线性边界的影响会增加计算难度，仿真结果难以收敛。本文采用Dytran软件在空间域上引入拉格朗日有限元法，时间域上采用非线性显式积分算法，对内凹型的膜结构进行有限元建模和数值仿真，选取合理的膜单元类型，有效避免了求解数值发散的问题，且计算效率高，过程易掌握，仿真结果对充气试验有一定的指导意义。

1 充气膜结构展开后承压过程求解思路

复杂外形可充气薄膜囊体结构的静承压仿真问题具有非线性问题的复杂性，利用解析方法很难对其进行有效的解答，但采用非线性有限元方法需进行针对膜类材料合理化的建模，避免了囊体材料的弯曲刚度、扭转刚度的影响。考虑膜材料承受法向力和面内拉伸力和剪切力的影响，针对非线性问题时间离散域的逐步迭代稳定性的问题[5]，研究数值计算结果的稳定性和材料稳定性的影响因素，针对材料表面的拼接处的缝隙，材料本身的通透性对气囊承压结果的影响，研究囊体气体内温度的差异性、内外气压的压差及对囊体结构承压性能的影响，具体流程如下：

a）针对充气膜结构的基本膜单元研究其基本特性，如薄膜不能抗弯[6]、抗扭、膜材正交性、小应变、大位移等的特点选择正确的材料和有限元单元；

b）研究非线性有限元离散求解过程的两种数值解法显式和隐式求解法的稳定性影响域和必要因素；

c）针对其复杂不规则外形内凹截面的特点，做初步的非线性隐式数值解法的试运算，查找引起数值解发散的原因；

d）针对充气膜结构进行进一步的方法研究和求解方法优选，完成基于气囊结构的安全气囊参数设置，完成其初始内外压、温度等基本参数的设置；

e）针对模型做显示积分法分析，调整时间步长和积分步，调整最大积分步长和积分时间以求得到计算成本、时间的最优；

f）对仿真计算结果进行进一步的理论验证和模型修正，为后续的充气膜结构折叠、展开过程做对比研究。

基于Dytran的一般承压强度显示仿真分析流程如图1所示。

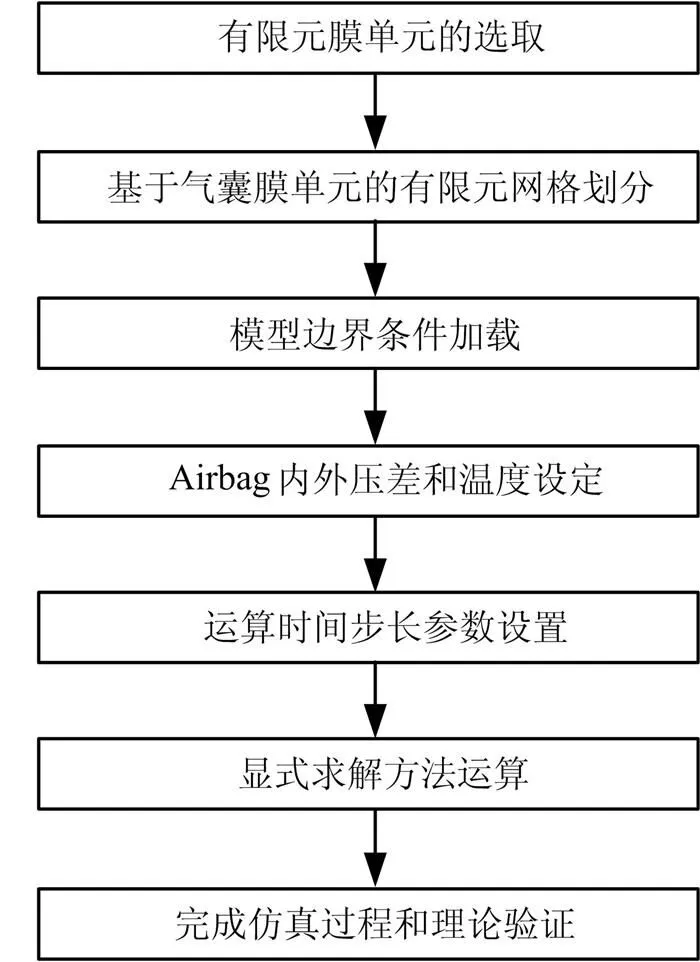
图1 基于Dytran的显示求解仿真分析流程

2 充气展开结构承压求解过程

2.1 气囊有限元模型的建立

气囊为一个环状结构，气囊皮内层为气囊的无纺布结构，气囊材料参数如表1所示。

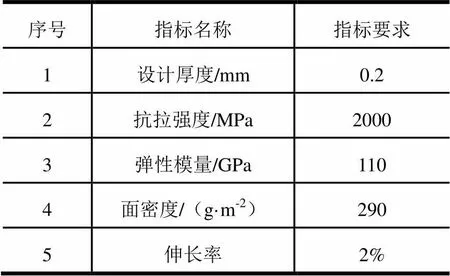
表1 囊体结构材料参数

气囊充气展开后三维图如图2所示。

图2 囊体结构三维示意

2.2 载荷边界及安全气囊参数设置

在囊体上端面胶粘接一个20 mm厚铝板，其承受的载荷为1.25 t。由于铝板面积与形状未规定，本文暂时以一矩形代替，铝板刚好能覆盖气囊。气囊下端与一无摩擦力气膜接触。气囊内部充有0.65 MPa的压强，气囊外部为真空状态，详细载荷工况参数见表2，在Patran中建立有限元模型，后处理选择Nastran软件初步建立有限元模型如图3所示。

表2 承压载荷工况参数

图3 囊体有限元模型

图3中，上板和下板均采用壳单元建模。上板模拟铝板，上板1.25 t的面载荷；下板模拟气膜接触，采用固支进行约束，上板与囊体采用接触载荷工况中的粘胶连接，模拟上板与囊体的胶结，下板与囊体采用接触载荷工况中的接触连接，模拟气膜接触，囊体内部均布受压。

囊体内侧在合并处通过进行有效粘结并通过缝纫等方法进行固紧，确保密封。囊体内圈边沿无充气，由于囊体充压过程中受施加均布压强的铝板垂向压迫，囊体垂向产生少量位移，而在平面内位移被固定，故在仿真计算时固定，向约束，放开向约束，效果见图4。

图4 囊体内圈x，y向固支图

在设置气囊的通透性时，应保证气囊通透性内外双向均可透气，安全气囊设置环境压强为真空状态，内压为0.65 MPa，初始温度300 K，气体常数286，具体设置界面如图5所示。

图5 Airbag设置界面

2.3 非线性仿真方法摸索

Shell单元板壳单元可以承受拉、压、弯、剪的平面单元，Membrane膜单元只承受拉压[7]，分析囊体材料为布结构，不承受弯剪力，只承受拉压载荷，并且囊体材料厚度仅为0.2 mm，非常细薄，故采用Membrane膜单元更能体现其力学特性。基于表1中的仅有的有限的材料参数，将膜材料当作各项同性的线弹性材料处理，模型采用膜单元，试算膜内部承受一个大气压时，采用Nastran线性静力学方法提交计算，软件报错，提示刚度约束不足，在下板上全部加上约束，依然没有解决这个问题，因此着手用其他单元尝试解决。若采用壳单元，内部承受一个大气压时，囊体最大应力约为1 480 MPa，变形量最大为8.6 mm。囊体外圈应力约为500 MPa，采用理论算法初步估算普通环形气囊外圈的平均张应力约为

由仿真计算囊体外圈的张应力结果与式（1）比较可知，仿真计算的应力与理论估算值相差很大，故采用壳单元建模计算不可取。囊体为薄膜结构，用膜单元建模最能体现受载情况，且膜单元内部充气为几何大变形问题，采用膜单元建模，非线性方法处理更符合真实情况。采用NASTRAN静力隐式非线性方法求解，单元出现不规则翘曲，求解结果无法收敛。

重新对模型进行建模，采用Dytran显式非线性求解器进行处理[8]，由于上板与囊体采用胶结，整个充压过程无拉开脱胶现象，胶结接触面积固定，但Dytran模块中接触无glue胶结设置，故在充气初始状态将上金属板与囊体之间的接触面采用共用节点模拟胶结，囊体与下板之间采用Contact接触模拟。Dytran中通过设置接触对防止两个面之间互相穿透，接触对的设置如图6所示。Dytran模块用CTRIA3来定义膜单元，膜单元只能承受面内载荷而没有弯曲刚度。三角形膜单元并非大应变单元，因而面内变形不能太大，膜单元只能承受弹性变形，囊体采用TRIA3三角形单元划分情况如图7所示。

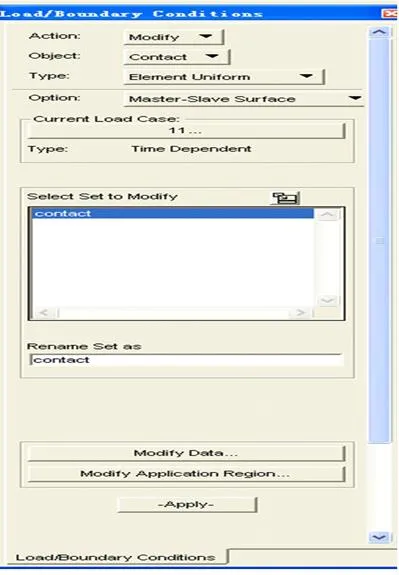
图6 接触对的设置

图7 囊体有限元划分局部

当充气的初始状态，气囊内部的气压为0.65 MPa，当充气过程中随着囊体内部空间的增大，囊体内部压强随空腔的体积膨胀会逐渐减小，如采用load界面的施加固定载荷的方式，载荷在充压过程没有改变，无法模拟内部压强载荷的实时变化，在模型中设置Airbag的方式施加内部载荷，并设置初始载荷的大小和作用区域，可以体现内部载荷跟随空腔变形的实时变化。

采用Dytran非线性显式求解方法求解，内压压强为0.65 MPa，初步设置计算时间为0.1 s、108步，最小时间步长为1×10-8。提交仿真运算，后期进行通过调节总时间步长，可使起始时间步长和最小时间步长逐步逼近最佳计算步长，节省计算成本。

2.4 仿真计算结果

针对以上计算流程得到的仿真结果如表3所示。

表3 仿真计算结果

由表3可知，在初始状态，内部处于均压状态，材料未发生变形，应力和应变为0，随着积分时间的增加，Dytran采用跟随算法，载荷逐步施加，变形增加，内部压强减小，变形变小，如此反复迭代，在时间最终状态变形达到最大值[9]。计算强度的参考值应考虑平均计算结果，计算平均状态的应力和变形的结果如图8所示。

a）应力俯视云图

b）应力局部云图

图8 囊体内压0.65MPa的应力云图

由图8可知，囊体结构边缘的最大应力局部达到1 350 MPa，整体平均应力水平约为200 MPa，囊体内边缘应力最大，囊体内圈在充压过程中会径向膨胀，但径向受约束作用，会产生反作用力压制囊体，因此囊体内圈有局部应力集中。囊体整体应力水平相对于囊体结构2 000 MPa的抗拉强度留有充足余量。式（1）根据普通的圆环模型进行剖面静力平衡，推导出剖面处的平均张应力，但此文研究的囊体模型非普通圆环，表面有局部凹陷，且囊体内圈和外圈均有沿，模型表面的复杂性和内外圈边界的结构特殊性使仿真结果与式（1）的推导结果不一致，说明对于不规则的囊体结构的仿真的必要性，而不能用简单的公式推导说明问题。囊体变形如图9所示。

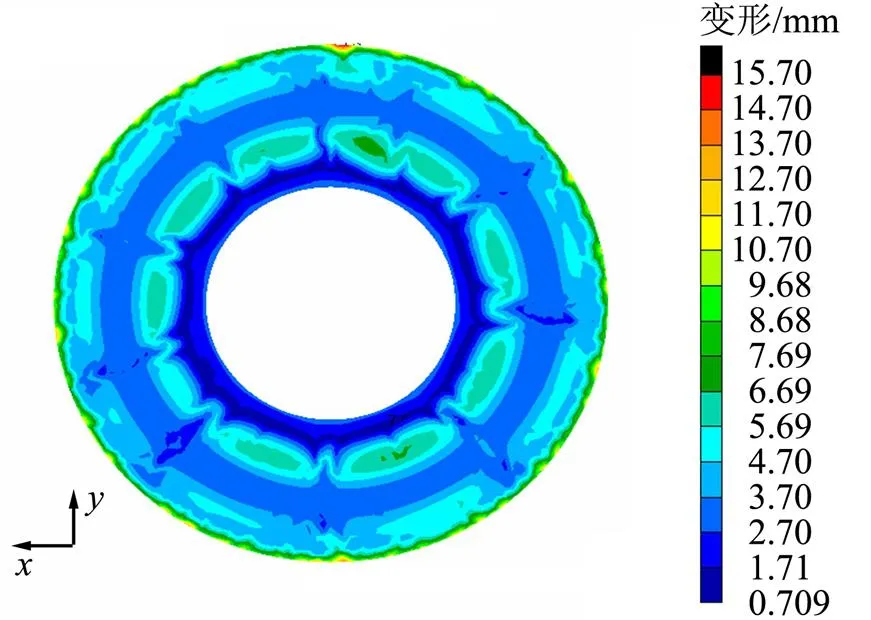
a）囊体俯视云图

b）变形仰视云图

c）变形局部视图

d）囊体向变形云图

续图9

由图9可知，囊体内压为0.65 MPa，变形量局部最大达到15 mm为囊体结构的外边缘处，由囊体外边缘充压状态张开造成。囊体上半圈由于受压板的压制作用相对于下板变形较大，囊体结构的平均变形为5 mm。囊体的内凹处由于受气体充压的影响，产生膨胀变形，内凹处鼓起。囊体+方向有11 mm左右的位移，-方向有6 mm左右的位移，表示囊体受垂向压力板的压迫作用和内部充压，产生膨胀变形。

通过以上基于Dytran的安全气囊内部承压仿真分析表明，应力计算结果满足材料强度要求，材料变形满足结构要求，仿真计算结果能够很好地展现气囊充压后的产品状态，对指导后期的充压试验以及气囊的优化设计具有较强的指导意义[10]。

3 结 论

a）本文针对囊体薄膜结构，在几何变形非线性条件下，预示其压差作用下的薄膜结构承载计算情况。采用Dytran软件，在空间域上引入拉格朗日有限元法，时间域上采用非线性显式积分算法，采用安全气囊均压法，成功而有效地模拟气囊充气承压的整个过程，有效突破外形内凹结构内部施加载荷的屈曲失效的计算瓶颈，为囊体结构承压强度校核开辟了新的思路。

b）针对局部内凹型复杂不规则截面的囊体薄膜结构，在多重复杂约束条件下，考虑其内部承压情况下的强度计算情况。此种仿真方法采用三角形膜单元建模，有效地规避了壳单元弯扭刚度的影响，并采用非线性显式积分法进行数值仿真，有效解决了大位移大变形问题、非线性载荷边界条件下的积分收敛的难题，并在计算时效上有效地调节自适应步长，节省了计算成本和时间。

c）针对几何非线性的内凹外形囊体结构，通过仿真分析判断壳单元与膜单元的取舍、线性方法与非线性方法的取舍，以及显式非线性方法与隐式非线性方法的取舍，有效地掌握了充气薄膜结构承静压强度校核的解决方法，为复杂外形气囊着陆器、空间气囊太阳帆板等结构的强度校核工作的开展提供了基础，拓宽了着陆器缓冲结构仿真研究领域。

d）基于Dytran的非线性安全气囊仿真方法研究，为后续囊体缓冲结构的充压试验提供重要参考依据，为囊体结构的优化设计提供参考和指导，节约了成本和周期，为囊体结构的折叠后充气可展开过程的数值仿真模拟提供重要技术基础和研究前提条件。

[1] 徐彦, 关富玲. 可展开薄膜结构折叠方式和展开过程研究[J]. 工程力学, 2008,25(5): 2-3.

[2] 何欢, 何成. 深空探测气囊着陆缓冲系统的原理样机冲击动力学相似问题研究[J]. 振动工程学报, 2013, 26(4): 10-11.

[3] Fushou L, Dongping J. Analytical investigation of dynamics of inflatable parabolic membrane reflector[J]. Journal of Spacecraft and Rockets, 2015, 52(1):1-2.

[4] 朱利君. 充气囊体结构变形及应力的数值模拟分析研究[D]. 上海交通大学硕士学位论文, 2014.

[5] 余莉, 程涵. 气囊充气过程流固耦合数值模拟[J]. 南京航空航天大学学报, 2010, 42(4): 4-7.

[6] 姬鸣. 薄膜天线支撑杆展开机构的研制[D]. 哈尔滨工业大学硕士论文, 2011.

[7] 麻震宇, 侯中喜. 临近空间大型柔性充气囊体结构特性分析[J]. 国防科技大学学报, 2015, 37(4):14-16.

[8] 袁中凡. 基于MSC.DYTRAN的安全气囊性能仿真分析[J]. 中国科技信息, 2008, 12(24):22-27.

[9] Mestreau E, Rainald L. Airbag imulation using fluid/structure coupling[R]. AIAA-96-0798, 1996.

[10] 卫剑征, 谭惠丰. 缓冲气囊展开与缓冲着陆过程的仿真分析[J]. 航天返回与遥感, 2010, 31(5): 4-5.

Non-linear Simulation Analysis of the Complex Sunken Airbag

Zhang Yan

(R&D Center, China Academy of Launch Vehicle Technology, Beijing, 100076)

As the large deformance and large displacement of the membrane structure, the bearing pressure analysis of the membrane structure is a complex numerical simulation process. If contact of membrane structure skin and the support part, and the limit constraint of membrane structure are considered, bearing pressure numerical simulation of membrane structure will be much complex and is very difficult to find an efficient theoretic resolution. This article use the non-linear explicit integral method to choose the proper membrane cell and settle the stability of the nonlinear discrete of the numeric process with the geometry nonlinearity and the contact. It provides a reasonable way to solve this kind of the membrane structure numerical simulation problem.

Membrane structure; Numerical simulation; Bearing pressure

1004-7182(2017)06-0016-05

10.7654/j.issn.1004-7182.20170604

V41

A

2016-07-07；

2017-09-05

张 妍（1984-），女，工程师，主要研究方向为结构动力学设计