基于接收信号强度指示的改进质心定位算法

谷 广，游 峰

(华南理工大学 土木与交通学院，广东 广州 510641)

0 引 言

在无线传感器网络(wireless sensor networks,WSNs)中，位置信息对传感器网络的检测活动至关重要[1]，对于定位而言，衡量定位效果优劣的指标包含精度和准确度[2]。目前，全球定位系统(global positioning system,GPS)能兼顾上述指标，但高能耗、高成本等问题，使其难以适用于WSNs。

WSNs定位算法主要分为基于距离和与距离无关两类[3]。基于距离的定位算法通过测量相邻节点间的距离或方位进行定位，能实现精确定位，但对硬件要求高，于是出现了距离无关定位算法。但距离无关算法定位精度不够高，针对该问题，各种提高定位精度的方法相继被提出。

文献[11]改进文献[12]的算法，提出了一种更为合理的权值选取办法。本文基于文献[11]，利用RSSI数据提出了一种改进的质心(improved centroid,ICentroid)定位算法算法。

1 质心定位算法

质心定位算法是一种基于网络连通性的室外定位算法。信标节点周期性地向邻居节点广播信标分组，未知节点收到来自不同信标节点的信标分组数量超过某一门限或一定时间后，即确定自身位置为这些信标节点所组成的多边形的质心

(1)

质心定位算法的精度与信标节点的分布以及密度有很大关系：

1)如图1(a)所示，未知节点位于△ABC质心位置O，质心算法定位准确；未知节点位于△ABC内其他位置如O1，质心算法会产生比较大的误差。

为此，从加权[13]、优选距离[14]和几何[15]等角度，各种提高精度的方法被提出。

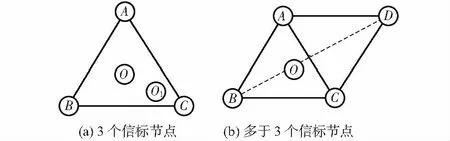
图1 质心定位算法原理

2 传播模型

无线电在空间传播不同程度的损耗会影响基于RSSI定位算法的精度。本文选用对数—常态分布模型对整个环境进行仿真研究

(2)

式中Pt为发送功率，一般0～4 dBm；Pl(d0)为经过距离d0后的功率，一般取d0=1 m作为参考点；η为路径损耗指数，取值范围一般为2～4；X(σ)为均值为0方差为σ2(通常取4～10)的高斯随机分布项。

3 改进算法

图1(b)所示问题由信标节点分布不均匀导致，本文算法原理如图2所示。

图2 优选节点原理

若未知节点O落在信标节点组成的△ABC内部O1处或边界O2处，此时存在

∠AO1B+∠BO1C+∠CO1A=360°

(3)

若未知节点落在△ABC外部(O3)，此时存在

∠AO3B+∠BO3C+∠CO3A<360°

(4)

AB,BC,CA为信标节点A,B,C之间的距离，为已知量；OA,OB,OC为未知节点O与信标节点A,B,C之间的距离，可以通过RSS值估计得到；因此,各角度值可以通过余弦定理求出

如上所述，计划生育政策的动员模式伴随着社会和经济的发展具有嬗变性。 从一元的强制命令发展为交往式的动员方式，交往式的动员模式更加关注个体的动机，凭借“交往+说服”促使个体产生内生性动力，若再配以外部的选择性激励，计划生育政策的实行会产生良好的社会效果和政治效果。 不过，计划生育政策终究锁定在“计划”二字，因此在市场经济体制下，以“说服”和“交往”为基石的动员式计划生育政策永远不会扮演决定性角色，而只能是一个不痛不痒的角色，它天然地依附于公权力强制的角色里。

(5)

由此可以得出未知节点O是否处于信标节点△ABC内部的判据：若

(6)

则未知节点O处于信标节点△ABC外部；若

(7)

则未知节点O处于信标节点△ABC内部或某一边上；直接采用

(8)

估计未知节点的坐标会产生比较大的误差，需要进行简单加权处理

(9)

4 算法步骤

基于上述思想，本文算法步骤如下：

1)信标节点周期性地向周围环境广播自身的节点ID、位置等信息。

2)未知节点根据阈值和接收的数据包，生成邻居节点表。

3)若未知节点的邻居锚节点数不小于3，执行改进算法；否则,执行步骤(4)。

4)若步骤(3)未能定位该未知节点，则用普通质心算法估计未知节点坐标。

5)若未知节点没有邻居信标节点，则将其归为不可定位节点。

6)计算定位误差

(10)

式中 (xi,yi),(Xi,Yi)分别为能被定位的未知节点的估计坐标和真实坐标；n为能被定位的未知节点数目；r为节点通信半径。

5 仿真结果

采用MATLAB进行算法仿真。在100 m×100 m的区域内随机散布100个无线传感器节点(包括未知节点与信标节点)，通过定位误差和无法定位节点数目两个指标比较算法之间的优劣。

图3 定位误差与信标通信半径关系

图3(a)～图3(d)为信标节点数目分别为20，30，40和50时，定位误差与节点通信半径的关系。①表示普通质心定位算法，②表示ICentroid算法。可以发现：

1)ICentroid算法比质心定位算法定位精度高，通信半径越大，精度提高越多。

2)普通质心定位算法定位误差随着节点通信半径增加，先减小后增大。由于随着通信半径增大，未知节点能探测到更远处的信标节点，使其邻居信标节点变得很不均匀，增大定位误差。ICentroid算法克服了此缺点。

3)随着通信半径的增加，ICentroid算法对定位精度的提高越来越小。因为通信半径大到一定程度后，大部分未知节点存在邻居信标节点，可以实现定位。

当信标节点数目为20和30时，无法定位未知节点数目随通信半径的变化如图4。②，③，①线分别表示普通质心定位算法、ICentroid算法、三边定位算法。

由图4可知，节点通信半径小于40 m时，基于RSSI的三边定位算法无法定位的未知节点数目远大于普通质心定位算法和ICentroid算法。因为三边定位算法或极大似然估计法定位要求未知节点至少能捕捉到3个及以上的信标节点数目，否则无法定位。而ICentroid算法对这一条件没有如此苛刻的要求。由此可见，ICentroid算法较三边定位或极大似然估计定位精度有所欠缺，但能增加可被定位节点的数目，降低因无法定位的节点带来的巨大误差。

图4 无法定位节点数目与通信半径的关系

6 结 论

本文的ICentroid定位算法，较传统质心定位算法定位精度有很大提高，较三边定位算法无法被定位的节点数有很大减小。ICentroid算法对硬件的要求不高，能较好地适应WSNs低成本等要求；算法思想可被用于改进近似三角形内点测试(approximate point-in-triangulation test,APIT)等与距离无关的定位算法，或采用DV-HOP算法中“用跳数估计距离”的思想替代用“RSSI来获得估计距离”的办法，实现真正的“与距离无关”的改进质心定位算法。

[1] 孙利民，李建中.无线传感器网络[M].北京:清华大学出版社，2005: 135-155.

[2] Dargie W,Poellabauer C.Fundamentals of wireless sensor networks[M].Hoboken:John Wiley & Sons,2010:249-263.

[3] 王 琼，候 男 ，孙 辉,等.神经计算融入多边测量法的机器人定位方法研究[J].自动化技术与应用，2016,35(2)：1-5.

[4] Nafarieh A,Ilow J.A testbed for localizing wireless LAN devices using received signal strength[C]∥Proceedings of the Communication Networks and Services Research Conference,2008.

[5] 赵 昭，陈小惠.无线传感器网络中基于RSSI的改进定位算法[J].传感技术学报,2009，22(3):391-394.

[6] 花 超，古小军，蔡 萍，等.基于RSSI差分修正的加权质心定位算法[J].传感器与微系统,2012,31(5):139-141.

[7] 朱忠记,何熊熊，章 晓.基于RSSI的四边测距改进加权质心定位算法[J].杭州电子科技大学学报,2014(1):17-20.

[8] 朱明辉，张会清.基于RSSI的室内测距模型的研究[J].传感器与微系统,2010，29(8):19-22.

[9] 吕 振，谭鹏立,一种基于RSSI校正的三角形质心定位算法[J].传感器与微系统,2010，29(5):122-124.

[10] 丁恩杰,乔 欣，常 飞，等.基于RSSI的WSNs加权质心定位算法的改进[J]. 传感器与微系统,2013，32(7):53-56.

[11] 刘运杰,金明录,崔承毅.基于RSSI的无线传感器网络修正加权质心定位算法[J].传感技术学报,2010，23(5):717-721.

[12] 陈维克,李文铎，首 珩，等.基于RSSI的无线传感器网络加权质心定位算法[J].武汉理工大学学报:交通科学与工程版,2006，30(2):265-268.

[13] 胡咏梅，张 欢.一种改进的无线传感器网络质心定位算法[J].计算机工程与科学,2012，34(2):45-49.

[14] 孙玮琢,迟 卫,王擎宇.加权质心定位误差的反向修正法[J].传感技术学报,2012,25(1):114-118.

[15] 朱 剑,赵 海，孙佩刚，等.基于RSSI均值的等边三角形定位算法[J].东北大学学报:自然科学版,2007，28(8):1094-1097.