一种新的四自由度SCARA机器人手眼标定方法*

陈 丹，白 军，石国良

(福州大学 电气工程与自动化学院，福建 福州 350108)

0 引 言

工业机器人以其精度高、稳定可靠、效率高等特点在工业上应用广泛，然而智能化、柔性化是制约其发展的瓶颈，机器人视觉系统的应用能够解决这些问题。机器人视觉系统分为Eye-in-hand和Eye-to-hand。Eye-in-hand视觉系统指相机固定在机器人关节上，随机器人一起运动的视觉系统。当机器人执行任务时，机器人关节上的相机采集工作视场信息，然后由计算机提取、转换为末端执行器和工作对象的相对距离，通过反馈距离信息，完成执行任务。若要视觉系统工作正常，需要知道相机坐标系与机器人坐标系之间的相对关系，即手眼关系。手眼关系标定是一项关键技术，标定精度直接影响到系统执行任务是否成功。许多学者在这方面做过很多研究，并取得成果，如Ma S D[1]提出了主动视觉的方法，利用消影点和平移向量之间的关系，只需3次平移就可以计算旋转矩阵，2次旋转和1次平移就可以计算平移矩阵； Ulrich M[2]引入螺旋理论代表空间任意运动，采用双四元数表示螺旋简化数学运算，通过标定板上特征点之间的约束和机器人运动规律同时求解旋转矩阵及平移矩阵；杨广林等人[3]通过对摄像机坐标系进行虚设旋转变换使旋转变换转化为平移问题，只需要2次平移运动和1次旋转运动就可以计算手眼关系；黄朝兴等人[4]利用主动视觉的方法标定旋转矩阵，结合激光笔确定特征点的世界坐标，标定平移矩阵。

然而，像SCARA有3个平行的旋转轴的机器人，许多要求做几组旋转轴不平行的旋转运动的方法并不适用，如Henrik Malm[5]和Shiu Y C[6]的方法要求做至少2组不同轴的旋转运动。本文以固高GRB—400四自由度SCARA机器人为研究对象，搭建机器人视觉系统，采用亚像素角点检测确定精确的特征点像素坐标，利用主动视觉的方法标定旋转矩阵，通过一个精加工的标准件—标定块，易准确地确定特征点的世界坐标，完成平移矩阵的标定。

1 固高GRB—400机器人

固高GRB—400机器人是典型的SCARA机器人，有3个旋转关节，其轴线(z轴)相互平行，另1个关节是移动关节，可以在平面内进行定位和定向，用于装配、抓取工作。机器人手眼系统结构如图1所示，采用D—H法建立机器人坐标系，得到末端执行器的位姿关系。

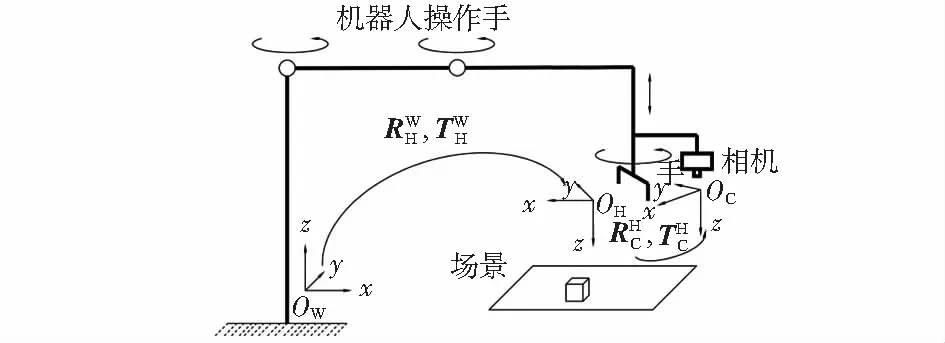
图1 手眼视觉系统结构示意图

2 手眼关系标定

2.1 手眼视觉系统中的坐标变换

如图1所示，X为空间中的任意一点，R为旋转矩阵，T为平移矩阵，通常用角标来区分不同的坐标系，角标W表示世界坐标系，H表示机器人末端执行器坐标系，C表示相机坐标系。坐标系之间的关系可以用式(1)、式(2)表示。式(2)是根据小孔成像模型得到

(1)

XC=zCM-1[uv1]T

(2)

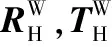
(3)

式中αx,αy分别为u轴和v轴上的尺度因子；(u0,v0)为图像中心;矩阵M通过MATLAB工具箱对相机进行标定得到;(u,v)为特征点X在图像上的像素坐标;zC为相机坐标系中特征点XC在光轴z上的投影，即深度信息;zC可由参考文献[3]给出的方法计算。

2.2 旋转矩阵标定

工作平台上贴有一打印的方格纸，取方格纸上的任意一交点X1，设其在执行器坐标系下的坐标为X1H，在相机坐标系下的坐标X1C，于是有

(4)

(5)

将式(4)代入式(5)，化简得

(6)

同理，做二次不同方向的运动，可得

(7)

(8)

写成矩阵形式有

(9)

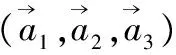
(10)

2.3 平移矩阵标定

取末端执行器在工作平台可达范围内的任意一点X2，其世界坐标记为X2W，代入式(1),得

(11)

将式(2)代入，得

(12)

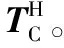
2.3.1 特征点世界坐标确定

特征点X2的世界坐标通过一个精加工的标定块来确定，标定块的示意图和机器人末端执行器示意图如图2所示，确定特征点X2的世界坐标原理如下：标定块两边槽的尺寸等于末端执行器的尺寸，并放置在贴有白纸的工作平台上，控制执行器将标定块夹住，然后控制执行器分别进行4次90°的旋转运动，每一次运动后将标定块的同一边缘用铅笔描在纸上，最后得到一个矩形，将矩形的对角线相连，交点即为特征点 ，即末端第三连杆轴中心在工作平台上的投影点，采取多次画矩阵，取多个中心点的中间点，以减少误差。第三连杆轴中心的坐标(x,y)可以从控制器中读出，已知平台高度，故可知特征点的世界坐标。

图2 标定块与末端执行器示意

2.3.2 特征点的图像像素坐标

图3 亚像素角点检测原理

3 实验结果与分析

实验采用的硬件主要有固高GRB—400机器人，USB2.0 CMOS 300万像素彩色数字相机，采集的图像大小为2 048×1 536，机器人控制柜，普通台式计算机，标定块。相机固定在机器人末端的执行器上，搭建的实验平台如图4所示。

图4 机器人手眼视觉系统

3.1 旋转矩阵标定实验

图5 检测到的亚像素角点

图6 控制台输出的实数坐标点

实验控制机器人完成4组运动，两两一组，如表1所示。实验结果如表2所示，误差由旋转矩阵与平均值作差所得，可以看到标定的旋转矩阵比较稳定，最大误差均小于0.004。旋转矩阵取平均值为

表1 4组平移运动次序

表2 旋转矩阵标定结果

3.2 平移矩阵标定实验

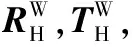
由于相机的光轴垂直于工作平台，工作平面上的特征点在相机坐标系下的深度值相等，所以沿用旋转矩阵标定实验中已计算出的深值，最后通过式(12)计算平移矩阵。同理，另外任取4个点作为特征点，利用上述方法多次求解，减少偶然误差,实验结果如表3所示，看到:实验结果比较稳定，最大误差均小于0.21。平移矩阵平均值为

3.3 标定结果测试

绘制测试用的方格纸，如图8所示，将纸贴在一个硬板上，呈任意角放在工作平台上，取4个特征点作为测试点，计算两点之间的距离，并与实际距离比较。最终的实验结果见表4。由表4可知:误差小于0.5 mm，精度较高，能满足工业应用需要。

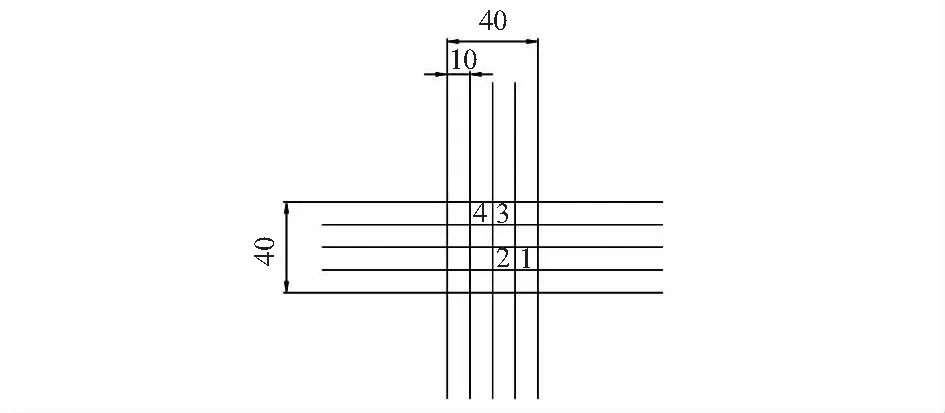
图8 绘制的方格纸

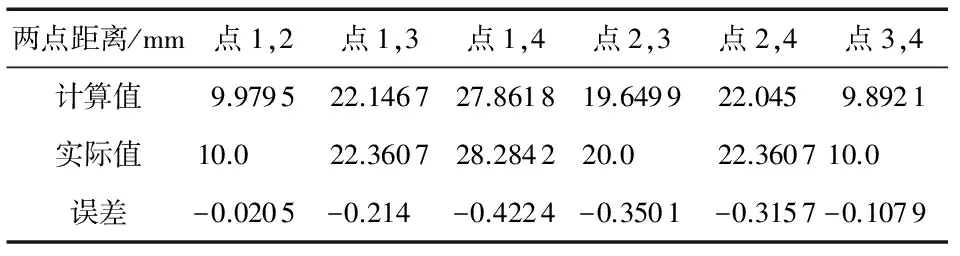
表4 不同特征点之间的计算距离与实际距离

3.4 对比实验

对文献[4]提出的方法进行了实验，该方法利用主动视觉的方法标定旋转矩阵，用激光笔辅助找世界坐标点，然后标定平移矩阵，实验场景如图9所示，选取工件平台上的4个点，用该方法标定的数据计算特征点之间的距离，实验结果如表5所示，可以看出误差小于0.7 mm。对比表4、表5知，本文方法精度高于文献[4]，文献[4]需先标定激光笔在末端执行器坐标系下的坐标，并要求激光笔垂直工作平面，增加了误差，降低了标定的精度。本文借助于标定块，利用几何知识，直接确定特征点世界坐标，简捷、易实现。

图9 对比实验场景

表5 文献[4]实验结果

表6列出了几种文献标定的精度，文献[1]的方法要求有二个不同的旋转轴，文献[2]标定精度较高，但是需借助于双四元数理论以及非线性优化，实现算法和具体步骤比较复杂，文献[4]标定精度高于文献[1]的精度，本文方法实现简单，精度较高。

表6 几种文献标定精度

4 结 论

利用精加工的标准件—标定块，通过几何作图的方法，精确快捷地确定末端执行器中心在工作平台上的投影点所对应的世界坐标，简化了求解世界坐标的过程，提高了平移矩阵的标定精度，采用亚像素角点提取算法，提取特征点的世界坐标，结合机械手平移规则，进一步提高了旋转矩阵的标定精度。实验结果表明：本文方法标定精度较高，可满足工业机器人的精确定位、普通抓取等作业。

[1] Ma S D．A self-calibration technique for active vision systems[J].IEEE Transactionsons on Robotics and Automation,1996,12(1):114-120．

[2] Ulrich M,Steger C.Hand-eye calibration of SCARA robots using dual quaternions[J].Pattern Recognition and Image Analysis,2016,26(1):231-239.

[3] 杨广林,孔令富,王 洁.一种新的机器人手眼关系标定方法[J].机器人,2006,28(4):400-405.

[4] 黄朝兴,陈 丹,唐旭晟.带激光笔的机器人主动视觉的手眼标定[J].微型机与应用,2015,34(17):70-74.

[5] Henrik Malm,Anders Heyden.A new approach to hand-eye calibration[C]∥Proceedings of the 15th International Conference on Pattern Recognition,2000:525-529.

[6] Shiu Y C,Ahmad S.Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the Form AX=XB[J].IEEE Transactions on Robotics & Automation,1989,5(1):16-29.

[7] 陈 丹,石国良.基于视觉几何的传送带测速方法研究[J].仪器仪表学报,2016,37(10):2307-2315.