基于改进PSO算法的移动机器人路径规划*
2018-01-26赵甜甜王思明
赵甜甜, 王思明
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
0 引 言
近年来,机器人技术发展迅猛,尤其是移动机器人在港口货物搬运、仓储物流方面取得了相当的成果。但工作任务的多节点特性使得移动机器人的路径规划成为其研究领域的重要分支。目前,粒子群优化(particle swarm optimization,PSO)算法、蚁群算法[1]、遗传算法、人工势场法是路径规划常用的方法。PSO算法的优点是计算量小,实时性好,结构简单,但容易陷入局部最优解产生死锁现象。文献[2]设计了一种将双混沌映射与自适应PSO算法相结合的混合算法,并通过仿真测试验证了其在解决传统PSO算法容易陷入局部最优点的良好性能[3,4]。文献[5,6]针对实际的工业问题,分别提出了基于莱维飞行的PSO算法和混沌优化与基本PSO算相结合的路径规划方法,并将其成功应用。
本文针对目前PSO算法在移动机器人路径规划方面存在的缺陷[7,8],提出了一种基于PSO算法和细菌觅食优化(bacterial foraging optimization,BFO)算法混合的路径规划算法,BFO算法中细菌以一定的概率迁徙到新的空间区域,其搜索方向随机变换,因此BFO算法全局搜索能力强[9]。基于此,本文采用PSO算法对机器人所处环境中的障碍物进行全局路径规划;在粒子群迭代的算法过程中使用BFO算法对机器人所处环境中的障碍物进行局部路径规划,并利用MATLAB仿真验证了混合算法的有效性和可行性。
1 环境建模
本文研究对象是机器人在已知环境下的路径规划,实际环境中的障碍物多是不规则的,为了便于研究将障碍物的各个边切线连接起来等效为矩形、三角形等规则形状。如图1所示,黑白二值位图代表机器人的运动场景,其中,障碍区为黑色,自由通行区为白色。在实际情况中机器人先通过传感器获取所处位置的环境信息,然后用MATLAB中的IMREAD命令将障碍物信息用矩阵表示;在矩阵中利用像素灰度值为255的点代表白色自由通行区域,而像素灰度值为0的点代表黑色障碍物区域。

图1 处理后的障碍物环境
2 PSO算法
假设存在一个能够搜索的n维空间,种群由m个单独粒子组成,并记为X=[x1,…,xi,…,xm]T,其中,第i个个体粒子的位置信息为xi=[xi1,xi2,…,xin]T;速度信息为vi=[vi1,vi2,…,vin]T;每一个粒子的个体极值表示为Pi=[pi1,pi2,…,pin]T;而用Pg=[pg1,pg2,…,pgn]T代表整个种群的全局极值。优化问题的可行解能够用每个个体粒子的位置信息表示,而适应度函数的取值很大程度上影响解的好坏;通常都要根据实际问题进行具体设计。
粒子的位置与速度以迭代方式进行更新
(1)
本文定义粒子的危险性系数为粒子各维的危险性系数之和
(2)
式中fi为粒子距离障碍物的最短距离之和,若无障碍物,则危险性系数为0。
第i个粒子的适应值函数即为对路径长度与路径危险系数以及粒子当前速度的共同约束,适应度函数定义为
fiti=αLpi+βdargeri+γvi
(3)
式中α,β,γ为对路径长度、粒子危险系数及粒子当前速度的加权系数。
3 BFO算法
3.1 BFO算法的基本操作
3.1.1 趋向性操作
细菌的趋向性操作以游走和翻转两种运动形式存在。趋化操作的步骤是:细菌先随机选择一个方向,然后向前游走一个单位步长,此时计算该位置的适应度值,如果适应度值劣于上一次位置的适应值,则随机选择一个方向翻转。翻转按照式(4)更换
P(i,j+1,k,l)=P(i,j,k,l)+C(i)φ(i)
(4)
(5)
式中P(i,j,k,l)为细菌个体i执行完第j次趋向性、第k次复制和第l次迁徙后的新节点位置;C(i)为细菌执行一次趋向性操作往前的步长;φ(i)为细菌翻转后进行方向调整选定的单位步长向量;Δ(i)为随机向量。
假设翻转后的适应值变优,则按照此时的方向继续进行游走运动,直到溢出给定的最大移动步数Ns或适应值不能继续优化为止。基于细菌感应机制的适应度采用Jcc表示
(6)
式中P(j,k,l)= {θi(j,k,l)|i=1,2,…,S}为菌群;dattract为引力深度;wattract为引力宽度;hrepellant为斥力高度;wrepellant为斥力宽度。在细菌感知规则的作用下,细菌的最终适应度将包含了细菌的感知适应度Jcc值。
3.1.2 复制操作
细菌的复制机会完全取决于其能量值的高低。为了保持种群数量稳定及尽可能地减少算法的运算量,规定了一种对半复制规则,不断淘汰能量低于50 %的细菌个体。因此,在BFO复制算子中一般设定细菌的规模数为偶数。
3.1.3 迁徙操作
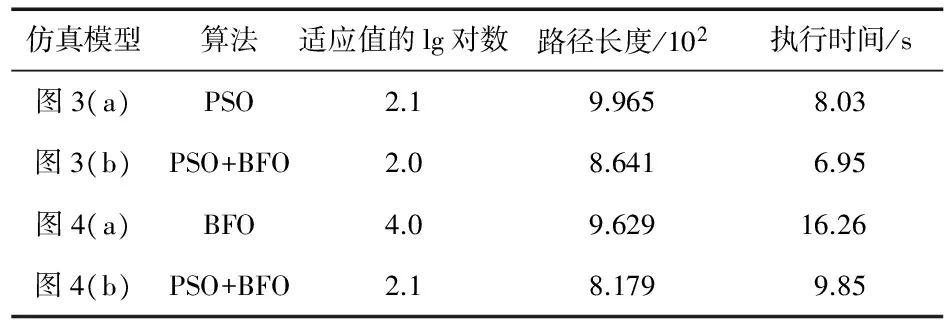
假设某个细菌完成了相应的繁殖活动,则赋予其一个进行迁徙的概率Ped,每一个细菌个体会随机产生一个[0,1]区域上的随机数Rand,若Rand 在执行优化算法的趋化操作步骤时,细菌随机翻转行为影响了细菌的寻优时间数(使其变长)。为了解决这一问题,引入具有环境感知能力的群体协作概念,保证了BFO算法寻优速度和精度与算法复杂度之间的平衡。 在算法的趋化算子中,细菌具有自我判断、自动调整的目标空间感知能力。为了提高细菌个体的寻优能力,将按照其适应度值的大小划分搜索方式:优于适应度值80 %的,追踪最优细菌个体进行搜索;劣于适应度值80 %的,通过追踪细菌群体中心位置进行搜索;如果两种方式均失效,则随机搜索;随机搜索失败,则将搜索方向调转180°,保证了算法具有一定的收敛速度。算法流程如图2。 图2 BFO算法优化设计 1)定义群体及个体的各变量:c1,c2为学习因子;w为惯性权重参数;Kmax为最大进化代数;X(k)为随机产生粒子群。 将当前进化代数的初始化值设为k=1,而粒子的初始位置和初始速度分别用x(k),v(k)表示,并规定个体继承属性,即原始最优位置(个体极值)也为初始位置。 2)将粒子当前位置信息代入适应度函数计算其当前适应值大小,群体极值的大小取决于适应度值最优的粒子位置信息。 3)在式(1)的作用下,不断计算每个粒子的位置信息和速度大小,生成下一代种群X(k+1)。 4)遍历比较粒子个体极值与不断更新后每个粒子的当前位置适应值,将适应值优的粒子当前位置作为其历史最优位置。 5)遍历对比所有粒子的个体极值与群体极值,将群体粒子最优位置用极值比较好的粒子当前位置信息替代;在迭代过程中,PSO算法的信息共享机制是算法陷入局部极值的主要原因。BFO算法中的趋化、迁徙操作的引入将有效改善PSO算法的全局搜索水平和收敛快速性,用来扩大搜索目标区域的粒子移动方向和前进步长,则可以根据翻转和游动2种方式来实现,避免其陷入局部最优解;如果粒子的迁徙概率满足迁徙条件,则将该粒子在目标区域随机扩散,保证种群有一定大小的搜索范围。 6)当满足迭代要求时,若k=Kmax,结束程序,此时会找到全局的较优解;否则,令k=k+1,返回步骤(3)。 利用MATLAB软件验证本文提出的PSO算法与BFO算法相结合的混合算法在移动机器人路径规划方面的可行性,并与单独的细菌算法和PSO算法对比。所选的参数如下:粒子数目m=50、学习因子c1=c2=1.531 2、最大迭代次数Kmax=1 000;细菌个数S=50、引力深度(吸引剂数量)dattractant=0.05、引力宽度(吸引剂的释放速度)ωattractant=0.05、斥力高度(排斥剂的数量)hrepellant=0.05、斥力宽度(排斥剂的释放速度)ωrepellant=0.05、复制的分裂数Sr=S/2、细菌的迁徙概率Ped=0.25。 图3(a)、图3(b)分别为传统的PSO算法、混合算法在地图模型一环境下的路径规划搜索轨迹,2种算法的迭代次数、适应值曲线如图3(c)所示。对比图3(a)~图3(c)可以看出,迭代次数在150以前,本文所提的混合算法路径规划结果在收敛速度、路径长短及适应值明显优于(适应值斜率较大)原始的PSO算法。粒子在坐标(250,150)遇到障碍物时,图3(b)的原始PSO算法陷入了局部最优值,而不是全局最优;对比图3(c)的混合算法,粒子跳出局部最优得到了全局最优。 图3 地图一模型2种算法路径规划效果对比 在地图二模型中,采用BFO法、混合算法的路径规划分别如图4(a)、图4(b)所示,2种算法的迭代次数、适应值曲线如图4(c)所示。由图4(a)~图4(c)可以看出,在迭代次数小于200时,混合算法的适应值基本趋于最优,而BFO算法由于搜索效率低,导致迭代时间长,并且得到的路径适应度降低。说明本文所设计的混合算法很好地提高了机器人对最优值的全局搜索能力和收敛速度。 图4 地图二模式下2种算法路径规划效果对比 表1给出了在不同的环境下,PSO,BFO及混合算法执行相同任务的相关特征值。混合算法能够有效地缩短最优路径长度与搜索时间。 表1 不同环境下各算法对比 以移动机器人为研究对象,将BFO算法的趋化、迁徙和复制操作引入到PSO算法中,得到一种具有全局搜索能力和快速收敛的混合路径规划算法。实验过程中分别使用PSO算法和BFO法对移动机器人进行全局路径规划,再与两者混合后的算法作对比分析。仿真研究表明,与传统的PSO算法相比,混合算法可以有效找到最优路径,并具有收敛速度快的特点。同时,本文算法陷入死循环的概率很小,可以有效避免陷入局部最优,在移动机器人路径规划的应用中具有一定的参考性和可行性。 [1] 何少佳,史剑清,王海坤.基于改进蚁群粒子群算法的移动机器人路径规划[J].桂林理工大学学报,2014,34(4):765-770. [2] 李明皓.基于混合离散粒子群算法的焊接机器人路径规划[D].上海:华东理工大学,2014. [3] 张万绪,张向兰,李 莹,等.基于改进粒子群算法的智能机器人路径规划[J].计算机应用,2014,34(2):510-513. [4] 翁理国,纪壮壮,夏 旻,等.基于改进多目标粒子群算法的机器人路径规划[J].系统仿真学报,2014,26(12):2892-2898. [5] 王学武,严益鑫,顾幸生.基于莱维飞行粒子群算法的焊接机器人路径规划[J].控制与决策,2017,32(2):373-377. [6] 梁 旭,刘才慧.基于混合粒子群算法的在线检测路径规划[J].国外电子测量技术,2015(12):30-34. [7] Wang J,Wu L J.Robot path planning based on artificial fish swarm algorithm under a known environment[J].Advanced Materials Research,2014,989-994:2467-2469. [8] Mandal P,Barai R K,Maitra M,et al.Path planning of autonomous mobile robot: A new approach[C]∥International Confe-rence on Intelligent Systems and Control,IEEE,2013:238-243. [9] Zhang Y,Gong D W,Zhang J H.Robot path planning in un-certain environment using multi-objective particle swarm optimization[J].Neurocomputing,2013,103(2):172-185.3.2 BFO算法优化设计
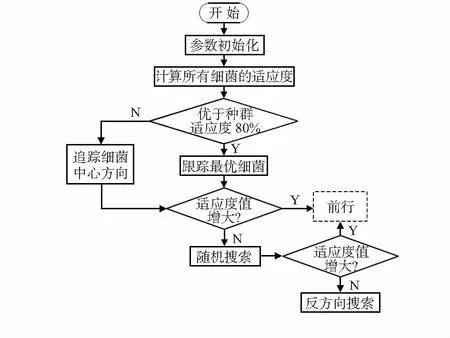
4 混合算法步骤
5 仿真分析


6 结束语
