机器人手灵巧操作中变接触点的几何求解方法

王耀飞，赵京东

(哈尔滨工业大学 机器人技术与系统国家重点实验室，黑龙江 哈尔滨 150001)

0 引 言

灵巧手的灵巧操作[1]过程中，为了实现被操作对象的位姿改变，灵巧手与被操作对象间相对位置关系必然发生变化，对应的灵巧手与物体的接触点也将发生变化，准确检测出接触点位置和接触力对于操作任务的完成具有重要的意义，文献[2]中利用触觉传感器设计了一种智能操作手柄，文献[3]通过在特定操作物体上贴装触觉传感器识别被操作物体上的接触点和接触力，文献[4]对于操作中接触面为凹面的接触问题专门设计了触觉传感器检测接触位置和接触力，文献[5]对触觉传感器在机器人操作中的应用有更全面的论述。

为了实现接触点的位置和接触力检测，除了触觉传感器，更为简单的一种方法是将灵巧手操作中接触点简化为固定[6]模型，即可仅由关节转角和关节所受力矩确定接触力。本文就固定接触点模型的误差进行了分析，并通过几何分析，建立了更为精确的接触点求解算法。

1 固定接触点的误差分析

如图1所示，手指在模拟将“钥匙”送出过程中，随着“钥匙”不断推出，手指的位姿不断变化，而接触点也由P1变化到P3。

图1 灵巧手模拟塞钥匙灵巧操作示意

灵巧操作过程中，如果不考虑接触点改变将至少在2个方面影响操作甚至导致操作任务失败：1)操作中的位移误差。如图2所示，手指对物体一次平移操作中，初始接触姿态下手指上F2与目标物体O2重合，而操作完成后的接触姿态下手指上F1与目标物体O1重合。不考虑接触面发生滑动的情况下，CAD测量出物体实际向下平移了70的距离，而手指上F1，F2的移动距离均不是目标物体实际移动距离，而且手指上这两点的移动轨迹均为不规则的曲线，而不是目标物体实际走过的一条竖直直线。因而灵巧手灵巧操作中必须考虑接触点变化，按照实际的变接触点规划灵巧手操作轨迹，才能实现精准的灵巧操作。2)操作中的接触力误差。

图2 灵巧操作中定接触点的位移误差

图3所示为DLR/HIT II灵巧手[7]末端剖面，图中手指内部1#部分为弹性体，该弹性体中间支柱两侧贴有应变片，实际对接触力的测量是将该弹性体受到的力矩转换为某个固定的理想接触点，随着灵巧操作的接触点变化，定接触点模型的接触力算法必然导致接触力误差。如图所示，若以F＇的作用点作为固定的理想接触点来计算实际接触力F的大小，由力矩关系知，算法必然导致接触力计算值的偏小，即导致实际灵巧手对目标物体施加过大的作用力，而对于相对于灵巧手较脆弱的目标，可能导致目标的破坏。

图3 灵巧操作中定接触点的接触力计算误差

由此可见，灵巧手灵巧操作中变接触点的分析与模型的建立具有重要的意义。当前研究中多采用触觉传感器来直接测量出接触点和接触力，但由于触觉传感器采用点阵式离散分布[8～10]，若间隙较大，在刚性接触下会出现无法准确检测接触点和接触力的问题，如图4所示。

图4 触觉传感器的离散分布

2 刚性接触下接触点求解算法

2.1 刚性接触下接触点的数学描述

如图5所示建立操作空间的笛卡尔坐标系Ow，手指的笛卡尔坐标系Of，手指末端关节的笛卡尔坐标系Ot，在指尖坐标系中建立接触面轮廓曲线{ft(x,y)}，并在操作空间坐标系中建立目标物体的接触面轮廓曲线{gw(x,y)}。

假定两个轮廓曲线对于其外部空间均为凸函数，而实际中灵巧手接触面轮廓对外部空间大部分的确是凸函数，现实中大部分被操作对象的轮廓面对外部空间也多为直线或凸函数(直线并不影响接下来的分析)。

设Of坐标系到Ow坐标系的变换矩阵Twf，Twf中的系数由操作空间中灵巧手的位姿决定，而在仅依靠灵巧手实现的灵巧操作中，手臂不发生位置变化，因而该变换矩阵系数均为常数。

设Ot坐标系到Of坐标系的变换矩阵Tft，Tft中的6个系数由灵巧手手指各个关节角度决定，本文灵巧手手指为三连杆机构，且末关节连杆与中间关节采用1︰1耦合运动，因而，该坐标变换由基关节俯仰角θ1和末关节俯仰角θ3完全决定。

设Ot坐标系中轮廓曲线{ft(x,y)}上一个点P坐标为[xt,yt,1]T，则操作空间Ow坐标系下该点坐标为[xw,yw,1]T，则有

(1)

经过以上坐标变换后，便可以得到操作空间下指尖外轮廓曲线{fw(x,y)}，因而灵巧手操作中刚性接触下接触点数学模型可以描述为：

空间坐标系下，手指以一定关节角度与目标物体发生接触，将该接触形态沿水平方向(或竖直方向)拉开一定距离，由手指接触面形成轮廓曲线{fw(x,y)}，由目标物体接触面形成轮廓曲线{gw(x,y)}，2个曲线水平(或竖直)距离最小的两个点即为刚性接触点。

由凸函数性质可知，当这两个曲线对其外部空间均为凸函数(或其中一个曲线为直线应一个为凸函数)时，刚性接触点有且仅有一个，把其定义为刚性接触点P1。

图5 刚性接触点的数学描述

2.2 刚性接触点的二分法求解

若在接触形态下2个轮廓曲线沿水平方向拉开一定距离，轮廓曲线1{fw(x,y)}和轮廓曲线2{gw(x,y)}分别为

(2)

(3)

取ymin和ymax分别为

ymin=max{min{yf 11,yf 21,yf 31,…},

min{yg 11,yg 21,yg 31,…}}

(4)

ymin=min{max{yf 12,yf 22,yf 32,…},

max{yg 12,yg 22,yg 32,…}}

(5)

根据凸函数性质可知，两个沿水平方向拉开的凸曲线间距d沿竖直方向构成了凸函数，因而求解d的最小值可采用二分法。具体迭代算法可用图6描述。

图6 二分法求解刚性接触点

3 仿真与结果分析

首先求出手指轮廓曲线，由于本文研究大量借助计算机的运算，因此,并未采用曲线拟合求曲线解析式，而是直接在手指的PRO—E模型剖面图中量出离散的48个点坐标(为了更高精度可以离散出更多的点进行求解)，参考系为手指末端关节的笛卡尔坐标系Ot，如图7所示。

图7 手指接触轮廓曲线离散化

如图8建立坐标系，其中Oa为灵巧手所在手臂的末端坐标系，可知，接触点的求解可以根据接触时两个接触轮廓拉开一定距离而变成求最小距离的问题，而图中被操作对象轮廓为一直线，因而,沿竖直方向拉开一定距离后，手指轮廓曲线再沿水平方向平移不影响接触点的求解，实验中,手指轮廓曲线的x,y坐标对求解毫无影响，只由轮廓曲线的旋转角度φ决定，有

φ=α+θ1+2·θ3

(6)

式中α为灵巧手所在手臂坐标系旋转角度；θ1为DLR/HIT II五指灵巧手手指基关节俯仰角；θ3为DLR/HIT II五指灵巧手手指末关节俯仰角。

图8 灵巧手平面操作的坐标系建立

由于灵巧手操作为手内操作，手臂不运动，φ完全由手指各关节角度决定，亦即手指末端接触点完全由手指关节角度决定，因此，给定灵巧手手指一个姿态后，采用二分法便可求出接触点。

设手臂转角130°，手指基关节旋转为0°～60°，手指末关节旋转0°～30°，用MATLAB进行求解，结果如图9所示。

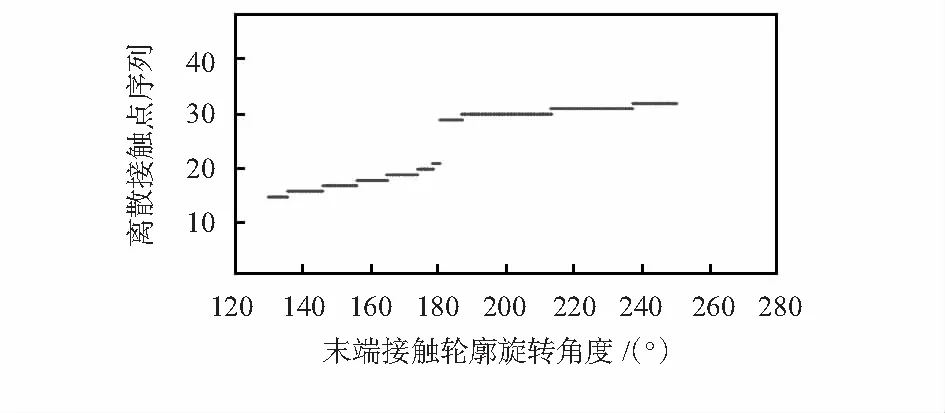
图9 特定操作下的动接触点与手指关节转角关系

对照图7可以发现：1)随着灵巧手操作末端姿态的旋转，接触点沿一个方向连续变化；2)特定的灵巧手接触面曲线和被操作物体的曲线下，并未与每个点均将发生接触，如图9中的离散接触点1～14与32～48在特定转角条件下并未与被操作物体发生接触，而由于接触点21～29为一条直线，只有当该直线与物体平面平行这一特定角度下才会接触，因此，离散求解中该段中间部分亦未发生接触。

4 结束语

本文通过建立手指接触面轮廓曲线和被操作对象的轮廓曲线，并根据手指与被操作对象的相对几何位置关系确定出刚性接触点的位置，由此得出灵巧手操作过程的变接触点求解算法，该算法理论上可以找出变接触点连续规律，而在计算机求解中也可以得到较触觉精度高的接触点。

[1] Bicchi A.Hands for dexterous manipulation and robust grasping:A difficult road toward simplicity[J].IEEE Trans on Robot,2010,16(6):652-662.

[2] 莫 沸,杨国胜,林英姿,等.基于自然接触传感器的智能控制手柄[J].传感器与微系统,2011,30(9):91-94.

[3] Masahiro Kondo,Jun Ueda,Tsukasa Ogasawara. Recognition of in-hand manipulation using contact state transition for multifingered robot hand control[J].Robotics and Autonomous Systems,2008，56(1)：66-81.

[4] 吕根波,李成刚,申景金.内凹面触觉传感器设计与接触过程分析[J].传感器与微系统,2015,34(8):21-25.

[5] Tegin J,Wikander J.Tactile sensing in intelligent robotic manipulation—A review[J].Industrial Robot:An International Journal,2005,32(1):64-70.

[6] Huang M B,Huang H P,Cheng C C,et al.Efficient grasp synthesis and control strategy for robot hand-arm system[C]∥2015 IEEE International Conference on Automation Science and Engineering(CASE),IEEE,2015:1256-1257.

[7] Liu H,Wu K,Meusel P,et al.Multisensory five-finger dexterous hand:The DLR/HIT hand II[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems,2008.

[8] 樊绍巍,刘伊威,金明河,等.HIT/DLR Hand II 类人形五指灵巧手机构的研究[J].哈尔滨工程大学学报,2009,30(2):172-177.

[9] Hanna Yousef,Mehdi Boukallel,Kaspar Althoefer.Tactile sensing for dexterous in-hand manipulation in robotics—A review[J].Sensors and Actuators A,2011,167:171-187.

[10] 张元飞.机器人灵巧手指尖柔性触觉传感器研制及操作研究[D]. 哈尔滨：哈尔滨工业大学，2012.