非线性多阶分数阶微分方程组正解的存在性
2018-01-26李辉来高瑞梅
代 群, 李辉来, 孙 艳, 高瑞梅
(1. 长春理工大学 理学院, 长春 130022; 2. 吉林大学 数学学院, 长春 130012)
分数阶微分方程在物理学、 化学、 工程学等领域应用广泛[1-4]. 文献[5-8]应用不动点定理研究了非线性微分方程正解的存在性和唯一性; Alsaedi等[9]研究了如下非线性时间分数阶微分方程组解的存在性和爆破解问题:
本文考虑如下非线性多阶分数阶微分方程组正解的存在性问题:
(1)
其中:
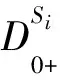
1 预备知识
定义1[3-4]函数y: (0,+∞)→的α>0阶Riemann-Liouville分数阶积分定义为
其中等式右端在(0,+∞)内有定义.
定义2[3-4]具有n阶连续导数的函数y: (0,+∞)→的α>0阶Caputo分数阶导数定义为
定义3[3-4]设K为Banach空间E中的一个闭锥, 在E中偏序≤定义为: 对于x,y∈E, 如果y-x∈K, 有x≤y, 则称(E,K)为一个偏序Banach空间.
定义4[3-4]对于x,y∈E, 偏序区间〈x,y〉定义为〈x,y〉={z∈E:x≤z≤y}.
引理1[3-4]设(E,K)是一个偏序Banach空间,x0,y0∈K,x0≤y0,F: 〈x0,y0〉→〈x0,y0〉是一个增算子, 且Fx0≥x0,Fy0≤y0. 如果F是一个连续紧算子, 并且K是一个正规锥, 则F在〈x0,y0〉中有一个不动点.

1) ‖Fu‖≤‖u‖,u∈K∩∂U1, 且‖Fu‖≥‖u‖,u∈K∩∂U2;
2) ‖Fu‖≥‖u‖,u∈K∩∂U1, 且‖Fu‖≤‖u‖,u∈K∩∂U2.
则F有一个不动点.
设空间X={u(t):u(t)∈C1[0,1]}, 在X中定义范数
‖u‖=max{|u(t)|>:t∈[0,1]}.
令
K={u(t)∈X:u(t)≥0, 0≤t≤1}.
显然,K是一个正规锥.
2 主要结果
引理3方程组(1)等价于如下积分方程组:
(2)
(3)
从而
同理可得方程(3).
算子F,G:K→K定义为
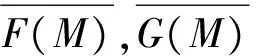
证明: 只需证明F,G:K→K是全连续算子.
首先, 证明F(M)是有界集. 令
则有
同理, 有
因此,F(M),G(M)是有界集.
其次, 证明算子F是等度连续的. 令u,v∈M, 对任意的0≤t1
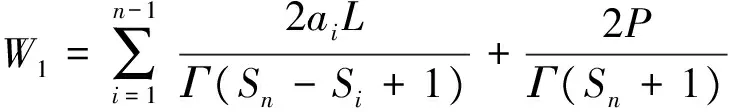
同理, 可得
|Gv(t1)-Gv(t2)|>≤W2|t1-t2|>Km-Km-1,
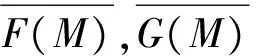
引理5u′<0,v′<0.
证明: 对方程(2)两边同时求t的导数, 有
同理, 有v′<0.

则方程组(1)有正解.
证明: 只需证明F,G有不动点即可. 由引理4,F,G是全连续算子. 对于0
从而Fu2(t)>Fu1(t). 同理可得Gv2(t)>Gv1(t). 因此,F,G是增算子.
由定理中的条件, 可得

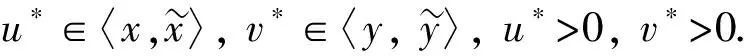

∀t∈[0,1].
令

则方程组(1)有正解.
证明: 令
对于u,v∈K∩∂U2, 有
∀t∈[0,1].
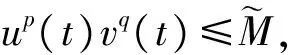
因此,
∀u∈K∩∂U2.
同理, 有‖Gv‖≤‖v‖, ∀v∈K∩∂U2.
另一方面, 对于u∈K∩∂U1, 有
∀t∈[0,1].
因此,
∀u∈K∩∂U1.
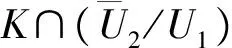
3 数值实验
例1考虑分数阶微分方程组:
由引理5,u′<0,v′<0, 有
u(0)≥u(t)≥u(1),v(0)≥v(t)≥v(1),
因此
η1/2v1/5(1)≤u1/2(t)v1/5(t)≤u1/2(0)v1/5(0),η=min{1,u(1)}.
又由定理2知, 该分数阶微分方程组存在正解.
[1] Kilbas A A, Srivastava H M, Trujillo J J. Theory and Applications of Fractional Differential Equations [M]. Amsterdam: Elsevier, 2006.
[2] Lakshmikantham V, Leela S, Jonnalagedda V D. Theory of Fractional Dynamic Systems [M]. Cottenham: Cambridge Scientific Publishers, 2009.
[3] Lakshmikantham V, Vatsala A S. Basic Theory of Fractional Differential Equations [J]. Nonlinear Anal, 2008, 69(8): 2677-2682.
[4] Sabatier J, Agrawal O P, Tenreiro M J A. Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering [M]. Dordrecht: Springer, 2007.
[5] DAI Qun, LI Huilai, LIU Suli. Existence and Uniqueness of Positive Solutions for a System of Multi-order Fractional Differential Equations [J]. Commun Math Res, 2016, 32(3): 249-258.
[6] DAI Qun, WANG Changjia, GAO Ruimei, et al. Blowing-Up Solutions of Multi-order Fractional Differential Equations with the Periodic Boundary Condition [J]. Adv Difference Equ, 2017, 2017: 130.
[7] 代群, 刘素莉, 李辉来. 非线性分数阶微分方程特征值问题正解的存在性 [J]. 吉林大学学报(理学版), 2015, 53(1): 1-4. (DAI Qun, LIU Suli, LI Huilai. Existence of Positive Solutions for Nonlinear Fractional Eigenvalue Problem [J]. Journal of Jilin University (Science Edition), 2015, 53(1): 1-4.)
[8] 李雪梅, 代群, 李辉来. 一类奇异非线性分数阶微分方程组正解的存在性与唯一性 [J]. 吉林大学学报(理学版), 2015, 53(2): 157-160. (LI Xuemei, DAI Qun, LI Huilai. Existence and Uniqueness of Positive Solutions for a Class of Singular Nonlinear Systems of Fractional Differential Equations [J]. Journal of Jilin University (Science Edition), 2015, 53(2): 157-160.)
[9] Alsaedi A, Ahmad B, Kirane M B M, et al. Blowing-Up Solutions for a Nonlinear Time-Fractional System [J]. Bull Math Sci, 2017, 7(2): 201-210.
