中国邮递员问题奇偶点图上作业法最优标准的商榷
2018-01-25王邦兆陈永清王海军魏志祥
王邦兆 陈永清 王海军 魏志祥

摘要:论文讨论了关于中国邮递员问题的一种误解,分析了产生误解的原因,提出了解决中国邮递员问题的指派问题模型。
Abstract: This paper discusses a misunderstanding about the Chinese Postman Problem, analyzes the causes of misunderstanding, and proposes a assignment problem model to solve the Chinese Postman Problem.
关键词:中国邮递员问题;奇偶点图上作业法;指派问题
Key words: Chinese Postman Problem; odd-even-point graphical operation method; assignment problem
中图分类号:O157.5 文献标识码:A 文章编号:1006-4311(2018)36-0258-02
1 中国邮递员问题与图上作业法
邮递员每天从邮局出发,走遍该地区所有街道再返回邮局,问题是他应如何安排送信的路线可以使所走的总路程最短。这个问题由中国学者管梅谷在1960年首先提出的,他给出了解法——“奇偶点图上作业法”,被国际上统称为“中国邮递员问题”。用图论的语言描述,给定一个连通图G,每边e有非负权),要求一条回路经过每条边至少一次,且满足总权最小[2]。中国邮递员问题的研究受到了国内外学者的广泛关注,国外最早研究中国邮递员问题的是J.Edmonds,他把中国邮递员问题称为Chinese Postman Problem(简称CPP)。国内研究中国邮递员问题的学者更多,产生了一批优秀的成果。冯俊文[3]提出了中国邮递员问题的整数规划模型,李念祖[4]提出了中国邮递员问题的完全最优子图算法,汪海森[5]等提出了中国邮递员问题的匹配算法,金毅[6]对中国邮递员问题进行了数理分析。
奇偶点图上作业法的基本思想:如果邮递员负责投递范围的街道图中没有奇点,它就是欧拉图,邮递员只要經过所有街道一次且仅一次,就能得到最短的路径;如果街道图中有奇点,将奇点两两配对,重复配对的两个奇点间的一条链,就可以得到欧拉图,如果重复的路径的总长度达到最短,就得到了最优解。
2 对奇偶点图上作业法最优标准的误解及其原因分析
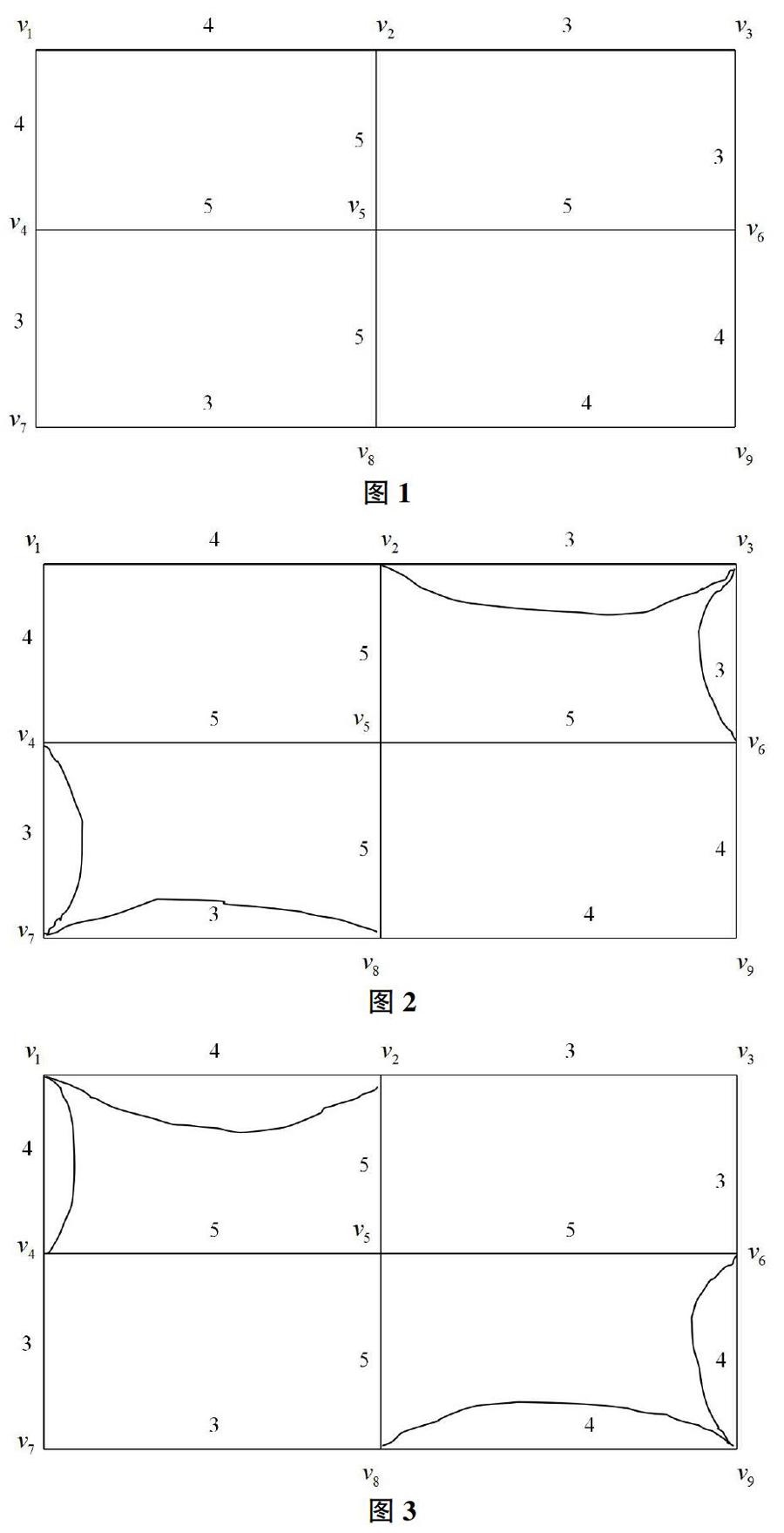
国内许多教材都出现了一处严重错误,以清华大学出版社的《运筹学》[1]为例,该教材(PP279-280)提出的奇偶点图上作业法的最优性条件为:①在最优方案中,图的每一条边上最多有一条重复边;②在最优方案中,图中每个圈上的重复边的总权不大于该圈总权的一半。这个最优性条件显然存在严重错误。图2和图3都完全满足上述最优性条件,两个方案的权重不一样,显然它们不会都是最优方案,图2的方案更优。
通过图2和图3的对比可以发现,这个“最优标准” 产生错误的原因是命题的大前提错误,也就是说,这个命题正确的大前提是奇点的配对方式正确。图1共有v2、v4、v6、v8四个奇点,只有将v4和v8配对、v2和v6配对,才有可能寻找到最优方案,其它的两种配对方式都无法得到最优解。
3 中国邮递员问题的指派问题模型与算法设计
根据奇偶点图上作业法的思想,首先应该选择正确的方式将所有奇点进行配对,重复配对的各对奇点间的最短路,就能得到最优方案。
解决最优配对的办法可以用Dijkstra算法和指派问题的模型予以解决,具体算法如下(假设图中共有n个奇点v1、v2、…、vn,n一定为偶数):
①用Dijkstra算法求出图中任意两个奇点间的最短距离dij和最短路;
②构建指派问题的模型:
所以,将v2和v6配对、将v4和v8配对,重复配对的奇点间的最短路,即可得到图2所示的最优方案。
参考文献:
[1]《运筹学》教材编写组.运筹学[M].三版.清华大学出版社,2005,6.
[2]管梅谷.关于中国邮递员问题研究和发展的历史回顾[J].运筹学学报,2015,9.
[3]冯俊文.中国邮递员问题的整数规划模型[J].系统管理学报,2010,12.
[4]李念祖.关于中国邮递员问题的最优完全子图算法[J].上海师范大学学报(自然科学版),2006,8.
[5]汪海森,林耿,卓彩娥.中国邮递员问题的匹配算法[J].长江大学学报(自然科学版),2013,9.
[6]金毅.对“中国邮递员问题”的数理分析[J].科技经济市场,2009(03).
