海浪随机过程模拟的快速算法

刘磊 郭晓芳

摘要：本文基于谱表示-随机函数方法，通过引入快速傅里叶变换（FFT）技术，发展了一类海浪随机过程模拟的快速算法，进一步提高了谱表示-随机函数方法的模拟效率，并与传统的Monte Carlo方法进行了对比分析。结果表明，引入FFT技术的谱表示-随机函数方法可在海浪随机过程的建模中获得令人满意的模拟效果，且所需的基本随机变量最少，模拟效率较高，生成的所有代表性样本构成一个完备的概率集，同时在模拟精度方面亦具有优势。

Abstract： This paper develops a fast algorithm for simulating the stochastic sea wave processes. According to the spectral representation-random function approach， the simulation efficiency of the proposed approach is greatly improved by applying the Fast Fourier Transform （FFT） technique. And the comparisons of the simulation results with the conventional Monte Carlo method are also presented in the paper. Numerical investigations indicated that a satisfactory simulation result can be obtained with minimum elementary random variables using the proposed approach. Meanwhile， all the representative samples can constitute a complete probability set. Numerical examples also revealed the significant advantages in terms of simulation accuracy.

關键词：谱表示;FFT技术;随机函数;海浪;随机过程

Key words： spectral representation;FFT technique;random function;sea wave;stochastic processes

中图分类号：P731.22;O324                            文献标识码：A                                  文章编号：1006-4311（2018）36-0205-03

0  引言

近年来，海浪灾害频发，给人类生产生活带来极大威胁，海浪灾害作用的研究备受关注，随着研究的不断发展，时至今日，国内外学者已提出了诸多模拟海浪灾害作用的方法[1]：物理模型法、几何模型法、粒子系统法和谱分析法。其中，谱分析法是以现有的海浪谱为基础，将海浪过程视为随机过程进行研究，谱分析法在实时性上能够满足一般的工程要求，且模拟结果具有一定的真实感，因而得到广泛的应用。

对于海浪随机过程的谱分析法研究，近年来，各国学者均取得了丰硕成果。Pierson[2]建立了海面位移随机过程与海浪谱之间的关系，开辟了应用海浪谱研究海浪随机过程的先河。俞聿修[3]采用谱分析法对一维海浪随机过程进行模拟，并取得了较好的模拟效果。张金春[4]等人通过对多种海浪谱的综合运用，克服了传统的谱分析法以单一海浪谱为核心所导致的频带范围局限性问题。杨怀平[5]和白连平[6]等结合方向谱模拟了三维海浪的实时过程，并对模拟效果进行优化，获得了较好的波面模拟效果。

上述应用谱分析法研究海浪随机过程均是以Monte Carlo方法为理论基础，均需要大量的随机变量才能保证其模拟精度，极大地增加了海浪随机过程模拟的计算量。为了克服这一困难，文献[7-9]进行了有益探索，引入随机函数的约束形式。进一步地，本文在谱表示-随机函数方法[10]的基础上，通过引入FFT技术，发展了一类海浪随机过程模拟的快速算法，实现了随机海浪过程的高效模拟。

1  谱表示-随机函数模拟的快速算法

1.1 谱表示-随机函数模拟方法

对于一个一维、单变量、零均值、实平稳随机过程X（t），基于正交随机变量的平稳随机过程的谱表示为[10]：

式中，Sx（ω）为随机过程X（t）的双边功率谱密度函数。ωk=kΔω，Δω为频率步长。{Xk，Yk}为一组标准正交随机变量[10]。

根据随机函数思想[8]，可定义{Xn，Yn}（n=1，2，…，N）为基本随机变量Θ的正交函数形式，即：

式中，Θ为在区间（-π，π）上均匀分布的基本随机变量。

然后，需将式（2）定义的标准正交随机变量{Xn，Yn}通过确定性的一一映射转换为式（1）中的目标标准正交随机变量{Xk，Yk}，即：Xn→Xk，Yn→Yk具体可参见文献[9]。于是便可得到一维、单变量、零均值的实平稳随机过程的谱表示-随机函数模拟公式，即[9]：

1.2 FFT算法的引入

研究表明，基于随机相位角的传统谱表示模拟方法，因其可引入FFT技术以高效地模拟海浪随机过程，故而得到广泛应用。基于这一认识，故式（3）可转换如下形式：

对比式（8）和式（3）可以发现，引入FFT技术后，式（8）中的频率求和项被FFT技术替代，从而极大地提高了随机过程模拟的计算效率。

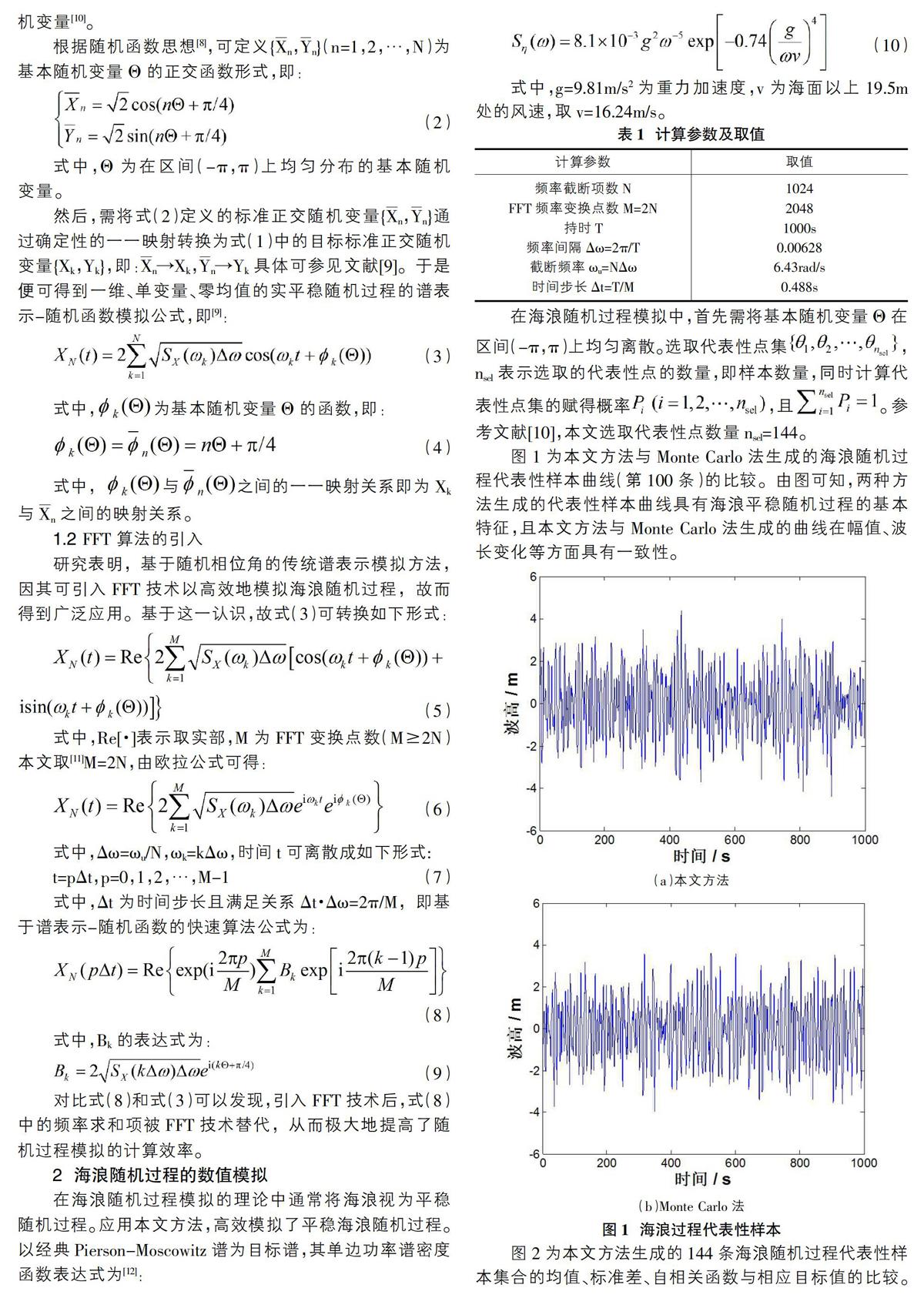
2  海浪随机过程的数值模拟

在海浪随机过程模拟的理论中通常将海浪视为平稳随机过程。应用本文方法，高效模拟了平稳海浪随机过程。以经典Pierson-Moscowitz谱为目标谱，其单边功率谱密度函数表达式为[12]：

综合表2、表3可以看出，在模拟相同数量的样本（如nsel=144条）时，模拟时间大致相同，但本文方法的均值相对误差及标准差相对误差均小于Monte Carlo方法，这是因为本文方法的基本随机变量是确定性抽样且在（-π，π）上均匀分布，而Monte Carlo方法则为随机抽样且概率不守恒，由此本文方法的模拟精度更高模拟效果更好。此外，本文方法生成144条样本与Monte Carlo方法生成1000条样本的模拟精度接近，但Monte Carlo方法生成样本时间大致是本文方法生成样本时间的14倍。更进一步地，从两种方法模拟所需的随机变量数量来看，本文仅需1个基本随机变量，而Monte Carlo法则需要N=1024个随机变量，并且，本文方法生成的144条海浪随机过程代表样本集合构成一个完备的概率集，这为基于概率密度演化方法实现大型复杂海洋结构的随机动力响应与动力可靠度精细化分析奠定了坚实基础。

3  结论

本文结合海浪Pierson-Moscowitz谱，基于谱表示-随机函数法，通过进一步引入FFT技术，实现了海浪随机过程的高效精细模拟。算例表明，本文具有如下特点：

①本文将FFT技术应用于谱表示-随机函数方法中来模拟海浪随机过程，可显著提高谱表示-随机函数方法的模拟效率，而且在模拟精度方面亦具有明显优势。

②本文方法不仅可实现海浪随机过程的快速模拟，且所需要的代表性样本数量少，每条代表性样本具有给定的赋得概率，所有的代表性样本构成一个完备概率集，进而可与概率密度演化方法相结合实现大型复杂海洋结构的概率密度演化分析。

参考文献：

[1]鄒建武，祝明波，董巍.海浪建模方法综述[J].舰船电子工程， 2010， 30（11）： 10-14.

[2]PIERSON WJ. An interpretation of the observable properties of sea waves in terms of the Energy of the Gaussian record[J]. Eos Transactions American Geophysical Union， 1954， 35（5）： 747-757.

[3]俞聿修.海浪的数值模拟[J].大连理工大学学报，1981，20（2）：84-90.

[4]张金春，陈志伟.基于海浪谱的东中国海海浪二维仿真[J]. 海军航空工程学院学报，2008，23（4）：449-452.

[5]杨怀平，孙家广.基于海浪谱的波浪模拟[J].系统仿真学报，2002，14（9）：1175-1178.

[6]白连平，陈秀真.三维随机海浪的数值模拟[J].海洋工程， 2000，18（4）：32-35.

[7]刘章军，方兴.平稳地震动过程的随机函数-谱表示模拟[J]. 振动与冲击，2013，32（24）：6-10.

[8]刘章军，刘玲.随机海浪过程模拟的随机函数方法[J].振动与冲击，2014，33（20）：1-6.

[9]LIU ZHANGJUN， LIU WEI， PENG YONGBO. Random function based spectral representation of stationary and non-stationary stochastic processes [J]. Probabilistic Engineering Mechanics， 2016， 45： 115-126.

[10]刘章军，张传勇，齐东春.高速列车乘坐舒适度评价的概率密度演化方法[J].振动与冲击，2018，37（14）：155-161.

[11]MASANOBY SHINOZYKA， GEORGE DEODATIS. Simulation of stochastic processes by spectral representation[J]. Applied Mechanics Reviews， 1991， 44（4）： 191-204.

[12]俞聿修，柳淑学.随机波浪及其工程应用[M].大连：大连理工大学出版社，2011.