聚酯熔体在喷丝孔中剪切流动对纺丝动力学的影响

张 帆，王建宁，陈 康，朱方亮 张玉梅，王华平

(东华大学 材料科学与工程学院 纤维材料改性国家重点实验室，上海 201620)

在纺丝过程中，为优化纺丝工艺、开发新技术和新产品，需要了解纺丝工艺与纤维结构性能之间的关系，虽然可以通过多次重复实验的方法来获得，然而，一方面，影响纤维结构和性能变化的工艺参数交互作用，远非单一因素的调整就能够达到优化纤维结构性能的目标，实验结果往往存在局限性；另一方面，在线检测困难且不全面，无法获得纺程上所有参数的变化路径，而变化路径对理解和预测纺丝过程中纤维非平衡态结构的形成至关重要，纺丝动力学模拟为路径变化的获得提供了最有效的手段。

熔体纺丝动力学模拟在模型不断优化的基础上，主要关注的是材料参数和纺丝工艺对动力学的影响，但是现有文献鲜有报道喷丝孔结构和尺寸对熔纺动力学的影响。作者主要研究喷丝孔的结构参数对聚酯熔纺动力学的影响。通过改变喷丝孔微孔直径(D0)及增加微孔出口倒角，分别计算得到了喷丝孔内熔体速度、速度梯度、压力和流线分布，以及纺程上丝条的速度、速度梯度、直径、温度、拉伸应力、取向和结晶分布，为喷丝孔设计和纺丝工艺优化提供依据。

1 熔体纺丝动力学模型简述

1.1 连续性方程

假定聚酯熔体为不可压缩流体，冷却介质为常压空气，忽略丝条与冷却介质之间的传质，挤出拉伸流动过程中的二维稳态连续性方程[1]如式(1)所示：

▽V=0

(1)

式中：▽为矢量微分算子；V为速度矢量。

1.2 动量方程

根据熔纺过程中的受力分析[2]，采用式(2)所示的动量方程：

(2)

1.3 能量方程

忽略丝条内辐射引起的温度变化[3]，能量方程表示为式(3)：

(3)

式中：Ta为吹风温度；h为传热系数；Cp为聚合物热容；D为纤维直径；T为纺丝温度；z为以喷丝孔入口为起点的纺程上任意一点距离；W为泵供量。

1.4 本构方程

Phan-Thien-Tanne(PTT)本构方程更适合描述聚合物熔体的流变特性[4-5]，非等温PTT模型的本构方程是用时间-温度叠加算法从等温PTT模型方程变化而来，其表达式如式(4)所示：

(4)

1.5 非等温结晶方程

忽略二次结晶以及生长晶粒的重叠[6]，非等温结晶方程如式(5)所示：

(5)

式中：K(T，f)为与温度和取向相关函数；Tmax是最高纺丝温度；Kmax是Tmax下最大结晶速率；d是结晶半高宽；C是应力诱导结晶系数；fa是分子取向因子。

1.6 取向方程

对于半结晶性高聚物,其取向包括晶区与非晶区的取向,表达式为式(6)～(8)：

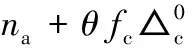
(6)

∆na=Copσ

(7)

(8)

1.7 边界条件

在熔融纺丝充分发展动力学的条件之下，熔纺成形动力学模型的边界条件如下所示[7]：

进口：

V=V(r)，τ=τ(r)，T=Ti

(9)

壁面：

V=0,T=Tw

(10)

自由面：

τn=0，Vn=0，qn=h(T-Tamb)

(11)

出口：

Vz=Vd，Fr=0，qn=0

(12)

对称面：

Vr=0，τ:nt=0，qn=0

(13)

式中：Ti是喷丝孔进口温度；Tw是喷丝孔壁面温度；Tamb是周围空气温度；n和t是法向和切向的单位矢量；q是热通量；Vd纺丝速度；Fr是径向的拉伸力；Vz是轴向速度；Vr是径向速度；r为径向方向。

1.8 材料参数

模拟所需的PET物性参数以及流变参数如表1、表2所示。

表1 PET物性参数Tab.1 Physical parameters of PET

注：ρ1为熔体密度；ρ2为纤维密度；Kp为热导率；∆α为晶体本征双折射率；∆β为无定形本征双折射率；∆Hf为熔融热；θ∞为最大结晶度；N为Avrami指数；T1为熔融温度。

表2 PET熔体流变参数Tab.2 Rheological parameters of PET melt

注：λ为松弛时间；δ为拉伸黏度有关系数；ζ为法向应力差有关系数。

用于纺丝模拟的工艺参数：W为0.255 g/min，T为290 ℃，Vd为6 000 m/min，Ta为25 ℃，吹风速度(Va)为0.4 m/s，吹风长度(La)为115 cm，吹风起点(L′)为5 cm，喷丝孔微孔长度(L)为0.8 mm，喷丝孔D0为0.3 mm，PET切片特性黏数([η])为0.65 dL/g。

2 结果与讨论

2.1 喷丝孔微孔D0对纺丝成形的影响

固定喷丝孔微孔L为0.8 mm,入口角(α)为45°，改变喷丝孔微孔D0分别为0.15，0.30，0.45，0.60 mm。根据1.8节所述PET物性参数和流变参数，以及纺丝工艺条件进行模拟研究。

从图1可以看出：喷丝孔微孔D0的变化对喷丝孔内的熔体挤出速度及压力分布造成很大的影响，在一定的熔体质量流速下，D0的变化会改变高聚物熔体的挤出速度；如图1a所示，在起初阶段，聚合物熔体处于蠕动状态，速度没有很大的变化，当流体接近出口管道时，速度开始剧烈的增加且不再重合，出口处的速度随着微孔D0的减小而急剧增加；如图1b所示，喷丝孔内产生的压力在z为9 mm左右时随着D0的减小而急剧增加，这是因为熔体在管道中流动，管道直径越小，流速越快，相应的压力越小。

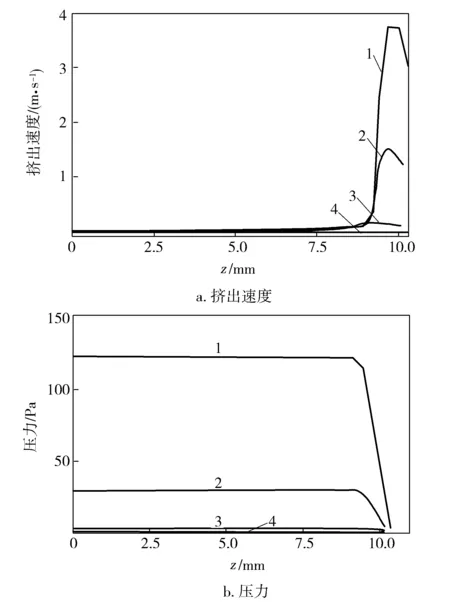
图1 不同微孔D0下喷丝孔内熔体挤出速度及压力分布Fig.1 Melt extrusion rate and pressure distribution in spinneret hole with different D0 of microhole1—0.15 mm；2—0.30 mm；3—0.45 mm；4—0.60 mm

由图2可以发现，D0的变化也会影响喷丝孔内的压力降(∆P)，当微孔D0小于0.20 mm时，高聚物熔体从喷丝孔内挤出产生的∆P较大，且随着微孔D0的增加而急剧下降。当微孔D0从0.30 mm增加到0.45 mm时，∆P的下降趋势较为缓和，且∆P的数值较小，这也说明熔体能够顺利地从喷丝孔内挤出。

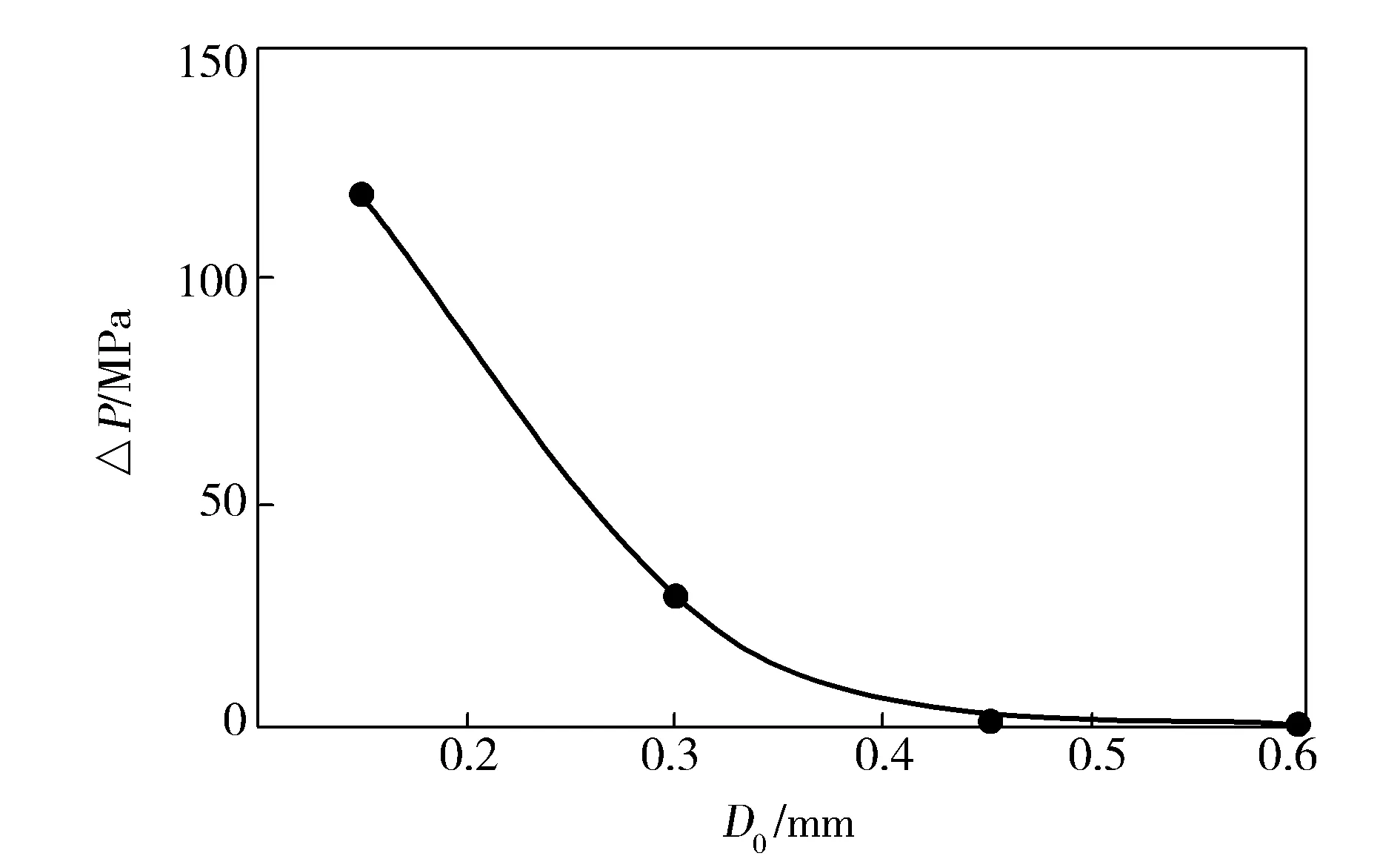
图2 ∆P与喷丝孔微孔D0之间的关系Fig.2 Relationship between ∆P and D0 of spinneret microhole

如图3所示，当聚合物熔体从喷丝孔挤出时会发生挤出胀大现象，丝条的直径先缓慢增加，然后逐渐减小到最终的数值并保持恒定，可以发现丝条起始位置的直径随着微孔D0增大而增大，但是丝条的最终直径是趋于一致的。同时，微孔D0的变化会对挤出胀大比造成一定的影响，随着微孔D0的增大，挤出胀大比快速地减小。在一定的质量流速下，增大微孔D0，会使熔体在管道内的流速减小，导致产生的剪切速率较小，因此储存的弹性能较少，挤出胀大现象减弱[8]。

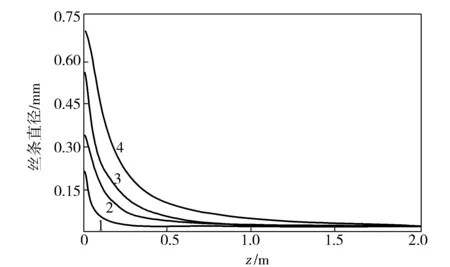
图3 不同微孔D0下纺程段丝条的直径分布Fig.3 Yarn diameter distribution along spinning line at different D0 of microhole1—0.15 mm；2—0.30 mm；3—0.45 mm；4—0.60 mm

由图4可知，虽然丝条直径的变化会对传热系数造成一定的影响，但是在空气段中丝条与外界环境之间的热交换过程主要取决于丝条与环境温度的差异[9]，因此丝条在空气段中的温度分布受D0变化的影响不大。

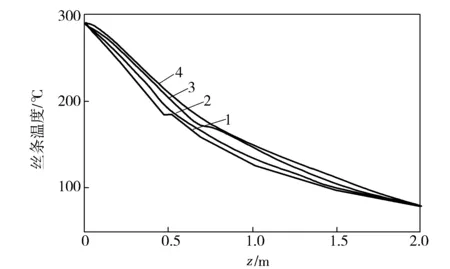
图4 不同微孔D0下纺程段丝条的温度分布Fig.4 Yarn temperature distribution along spinning lineat different D0 of microhole1—0.15 mm；2—0.30 mm；3—0.45 mm；4—0.60 mm

由图5可以看到，微孔D0越小，纺程上丝条速度上升越快，速度梯度越大，但是丝条最终速度是趋于一致的。这是因为随着D0减小，行程上纤维的冷却速率增加，使得纤维温度下降更快，从而拉伸黏度增加，纤维速度和速度梯度均增加。

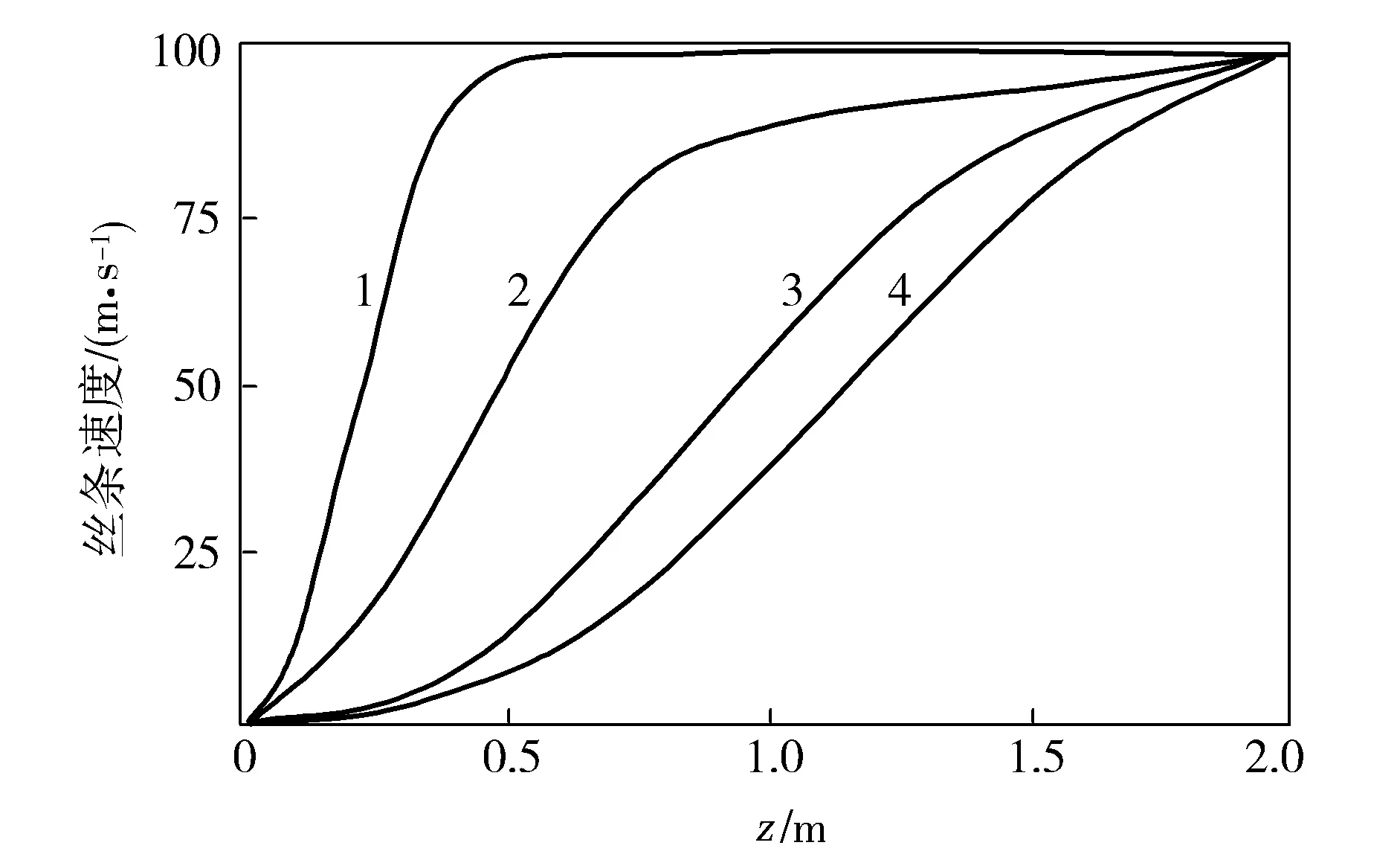
图5 不同微孔D0下纺程段丝条的速度分布Fig.5 Yarn velocity distribution along spinning line at different D0 of microhole1—0.15 mm；2—0.30 mm；3—0.45 mm；4—0.60 mm

从图6a可以看出，纺程段丝条的拉伸应力随微孔D0的减小而增大，应力大小取决于纤维的拉伸黏度大小，纤维的直径越小，在相同纺程位置其温度越低从而使拉伸黏度越高，因此所受拉伸应力也随之增大。而应力诱导取向，取向诱导结晶，因此应力的变化也会对纤维在纺程的结晶和取向产生影响[10]，应力越大，内部分子排列越容易趋于一致，纤维取向程度越高，结晶程度也越高。从图6b和图6c可知，随着微孔D0的减小，丝条在纺程上的结晶和取向程度会越高，且取向和结晶的位置均向喷丝孔方向移动，这也是因为应力的增大，导致取向和结晶位置前移。

图6 不同微孔D0下纺程段丝条的拉伸应力以及θ和∆n的分布Fig.6 Tensile stress and θ and ∆n of yarn along spinning line at different D0 of microhole1—0.15 mm；2—0.30 mm；3—0.45 mm；4—0.60 mm

2.2 喷丝孔出口倒角对纺丝成形的影响

喷丝孔出口倒角对喷丝孔内熔体的速度、速度梯度、压力分布影响不大，其影响主要发生在纺程段。采用微孔L为0.8 mm，微孔D0为0.30 mm，入口角α为45°,并且带有出口倒角的喷丝孔进行研究。模拟涉及到的PET物性参数及纺丝工艺条件同1.8节所述。

从图7可看出，有出口倒角的情况下丝条直径变化更快，但是丝条最终的直径与无倒角的情况是一致的，这可能与出口倒角有利于释放熔体在喷丝孔中积累的能量，使得纤维更易拉伸有关。

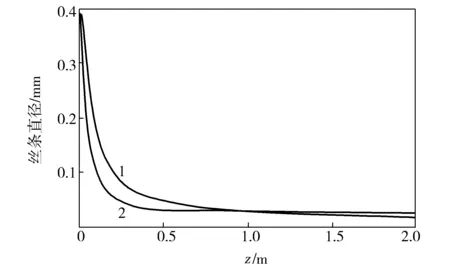
图7 喷丝孔有无出口倒角时纺程段丝条的直径分布Fig.7 Yarn diameter distribution along spinning line using spinneret hole with or without outlet chamfer angle1—无出口倒角；2—有出口倒角

从图8a可以看到，增加出口倒角时，丝条温度下降更快，从而导致开始结晶位置更加靠近喷丝孔。由图8b可以看到，增加出口倒角，对丝条最终速度并没有影响，但是会增加纺程上丝条的速度梯度。因为增加出口倒角，使得纤维降温更快，从而导致拉伸黏度增加，纤维更易被拉伸。

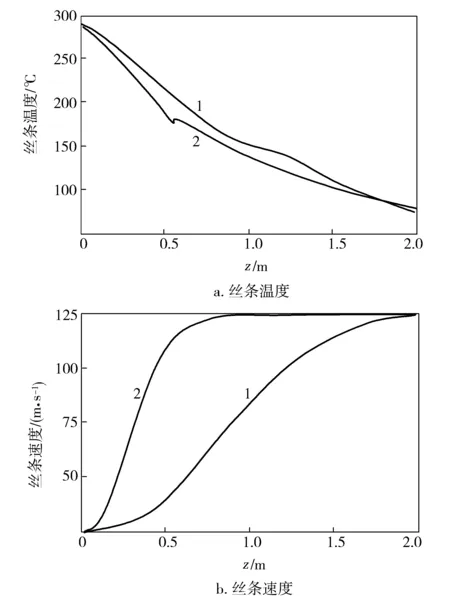
图8 喷丝孔有无出口倒角时纺程段丝条的温度及速度分布Fig.8 Yarn temperature and velocity distribution along spinning line using spinneret hole with or without outlet chamfer angle1—无出口倒角；2—有出口倒角

较大的拉伸黏度会使丝条的拉伸应力增加，而喷丝孔有出口倒角的情况下，丝条温度下降更快，从而导致丝条的黏度增加，因此拉伸应力也随之增加，如图9a所示。应力诱导取向，取向诱导结晶，因此纺程上丝条的∆n和θ都有不同程度的提高，并且在有喷丝孔有出口倒角的情况下会使丝条发生取向和结晶的位置更加靠近喷丝板,如图9b和图9c所示。

图9 喷丝孔带有出口倒角时纺程段丝条的拉伸应力以及∆n和θ分布Fig.9 Tensile stress and ∆n and θ of yarn along spinning line using spinneret hole with or without outlet chamfer angle1—无出口倒角；2—有出口倒角

此外，增加出口倒角对挤出胀大也有影响，经过计算可以得到，无倒角的情况下丝条的挤出胀大比为1.36，而有倒角的情况下丝条的挤出胀大比为1.27，说明增加出口倒角可以降低纺丝过程的挤出胀大现象，因为增加出口倒角有利于熔体的弹性能耗散，因此残留的弹性能较少，挤出胀大现象也随之减弱。

3 结论

a. 采用建立的动力学模型，探讨了喷丝孔结构，包括喷丝孔微孔D0和出口倒角对涤纶熔纺动力学的影响。改变喷丝孔微孔D0能够有效地调控喷丝孔内熔体挤出速度和压力降，从而改变挤出胀大比和拉伸应力。微孔D0减小，丝条的拉伸应力、∆n和θ均有不同程度的增加。

b. 微孔出口倒角主要影响纤维在纺程段的结构与性能，对喷丝孔内的熔体流动影响不大。增加出口倒角，可以削弱纺丝过程的挤出胀大现象，增加熔体可纺性；温度的快速下降导致开始结晶位置更加靠近喷丝孔，拉伸应力、∆n和θ都有不同程度的提高，并且会使发生取向和结晶的位置更加靠近喷丝板。

参 考 文 献

[1] Bostwick C O.The effect of spinneret hole length on fiber diameter; A means for measuring polymer solution inhomogeneities[J]. Text Res J,1962,32(10):819-824.

[2] 叶敬平.涤纶FDY熔融纺丝模拟研究[J].合成纤维工业，2012，35 (6):50.

Ye Jingping.Simulation of melt spinning process of polyester FDY[J].Chin Syn Fiber Ind,2012，35 (6):50.

[3] 李楠帆.细旦涤纶长丝熔融纺丝动力学工程模型研究及应用[D].上海：东华大学,2012.

Li Nanfan.Research and application of melt spinning dynamic engineering model for fine-denier polyester filament[D].Shanghai:Donghua University,2012.

[4] Ziabicki A,Jarecki L,Wasiak A. Dynamic modelling of melt spinning[J]. Comput Theor Polym Sci,1998,8(1/2):143-157.

[5] Patel R M,Bheda J H,Spruiell J E. Dynamics and structure development during high-speed melt spinning of nylon 6.Ⅱ. Mathematical modeling[J].J Appl Polym Sci,1991,42(6):1671-1682.

[6] Jeon Y P,Cox C L.Modeling of multifilament PET fiber melt-spinning[J]. J Appl Polym Sci,2008,110(4):2153-2163.

[7] Revenu P,Guillet J,Carrot C.Elongational flow of polyethylenes in isothermal melt spinning[J]. J Rheol,1993,37(6):1041-1056.

[8] Ziabicki A.Mechanical aspects of fibre spinning process in molten polymers-Part Ⅲ: Tensile force and stress[J]. Colloid Polym Sci,1961,175(1):14-27.

[9] Ziabicki A.Crystallization of polymers in variable external conditions.Ⅱ. Effects of cooling in the absence of stress and orientation[J].Colloid Polym Sci,1996,274(8):705-716.