功率模块引线键合界面温度循环下的寿命预测*

郭源齐，高 涛，许杨剑*，梁利华，刘 勇

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.中国联合工程公司，浙江 杭州 310052)

0 引 言

引线键合是功率模块中最常用的一种电气互联方式[1]。在实际应用中，功率模块必须具有较高器件强度以及可靠性[2]。

关于功率模块寿命预测方面的研究，HUNG等人[3]针对功率模块引线键合部位在功率循环下的失效情况进行了研究，通过实验与数值仿真相结合的方式，对引线键合界面在功率循环下的疲劳寿命进行了预测；谢鑫鹏等[4]通过实验的方式，对键合工艺参数进行了优化分析，同时运用能量法对芯片粘贴焊层的寿命进行了预测。以上学者从经典的寿命预测理论角度，依靠经验公式对功率模块进行寿命预测，虽然简单方便，但存在一定的局限性，即不能对功率模块的失效过程有所了解。为此，本研究将提出一种基于循环内聚力模型的寿命预测方法，以弥补传统方法在描述失效过程中的不足。

本研究将对不同封装材料下的功率模块进行温度循环实验，构建封装体整体的有限元模型，利用子模型法，结合基于应变的疲劳寿命预测理论，对不同封装材料下引线键合界面的疲劳寿命进行预测。

1 寿命预测方法

1.1 塑性应变主导的经验寿命预测方法

在电子封装的疲劳失效研究中部件的疲劳失效归纳为两类，分别为低周疲劳与高周疲劳。有学者研究发现[5]，部件疲劳寿命的高低主要取决于总体的应变幅大小。而总体的应变幅由塑性应变幅和弹性应变幅两部分组成，疲劳寿命水平分别取决于其塑性应变幅水平和弹性应变幅水平。其寿命预测公式为：

(1)

(2)

(3)

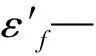
电子封装测试中可以忽略弹性应变的影响，有学者提出了基于塑性应变幅值的经验方程：

Nf=C1εC2

(4)

式中：C1，C2—两个待定参数，与具体的结构、材料以及测试条件有关。

1.2 基于内聚力模型和损伤演化理论的寿命预测方法

内聚力模型首先由DUGDALE和BARENBLAT[6-7]提出。内聚力模型根据其本构关系的不同可以分为多种，包括双线性内聚力模型[8]、指数型内聚力模型[9]、梯形内聚力模型等[10]。在本文中运用的循环内聚力模型的张力—位移关系是双线性内聚力模型。在考虑损伤的情况下，其本构关系如图1所示。

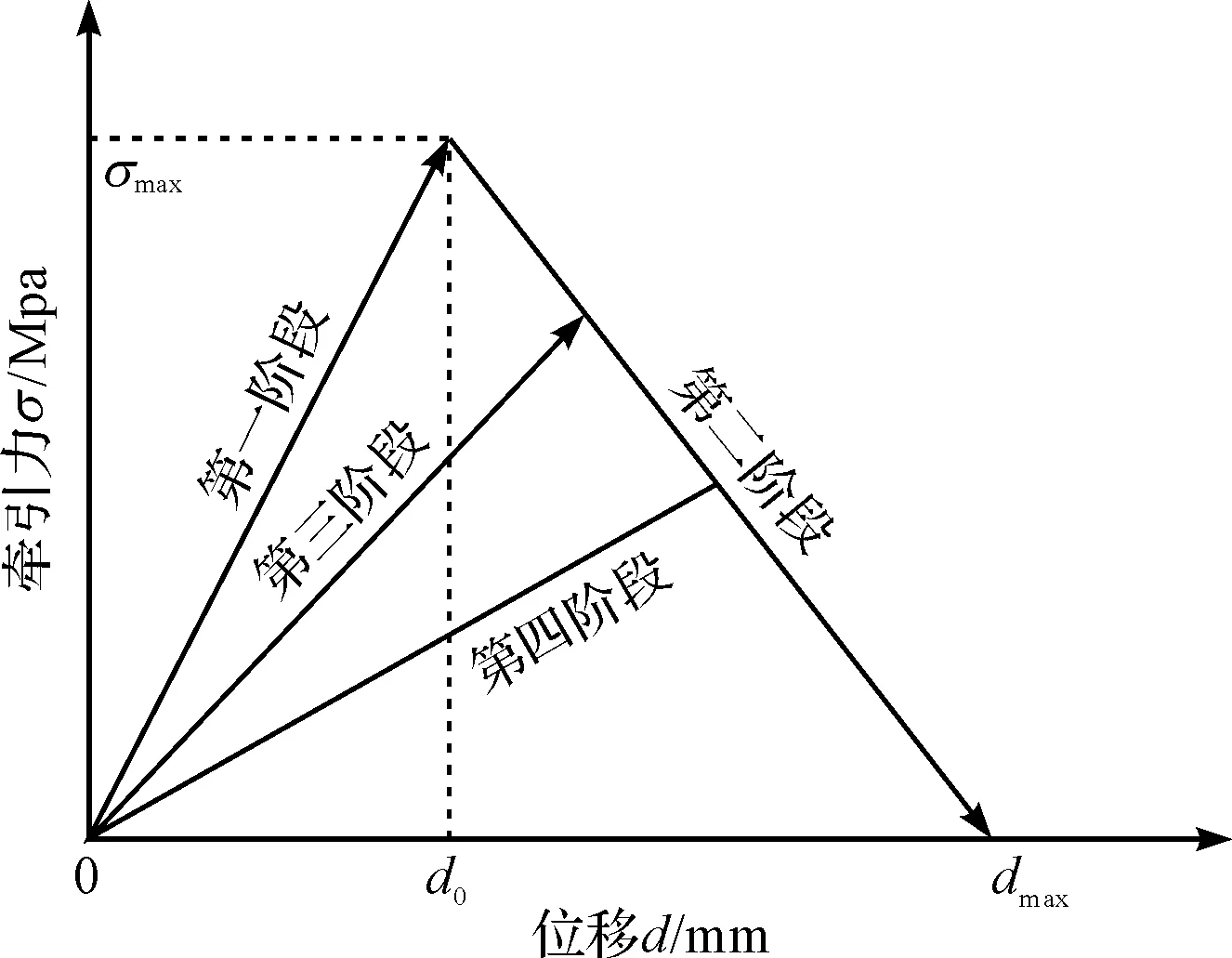
图1 双线性内聚力模型

图1中，第一、二阶段可以看作是单调拉伸的加载阶段，第四阶段为卸载阶段，第三阶段为发生损伤后的重新加载阶段。假设加卸载过程都是线性的，则牵引力Tt与张开位移dt的本构关系为：

(5)

式中：Dl—损伤因子，两次加载过程中材料刚度的不同便是由损伤因子引起的。

根据SIEGMUND[11]的损伤理论，在循环加载的情况下，内聚力模型会发生应力退化，其最大应力σmax、τmax与损伤因子Dl之间的关系为：

σmax=σmax,0(1-Dl)，τmax=τmax,0(1-Dl)

(6)

式中：σmax,0，τmax,0—初始的最大法向、切向应力。

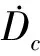
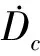
(7)

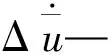
(8)

最终，将疲劳损伤与单调损伤累加，即可得到总体的损伤值Dl：

(9)

将上述的张力—位移关系、损伤准则通过Abaqus的UEL接口，编制相应的程序，运用于模拟中。

2 温度循环失效实验

2.1 实验原理及过程

温度循环实验依靠温度循环试验箱，将试样交替地置于温度差异巨大两个试验箱中一段时间，以形成温度交替变化的温度场，从而对试样在严苛环境下的承受能力进行评估。在交替变化的温度载荷作用下，由于芯片与引线材料之间热膨胀系数的不匹配，导致在芯片的引线键合界面处容易产生较大的塑性应变，在这种随着温度变化的塑性应变作用下，界面最终发生疲劳失效。

在本研究中，采用JEDEC-JESD22-A104C标准，对3种不同封装材料的功率模块进行热循环实验，每种封装材料的试样各10个，同时放入实验箱中，分别在进行了200，500，700，1 000及1 200次循环后取出，考察其失效情况。每个循环周期的时间为30 min，高低温之间的转换时间为5 min，高低温保持时间为10 min。

温度载荷的示意图如图2所示。

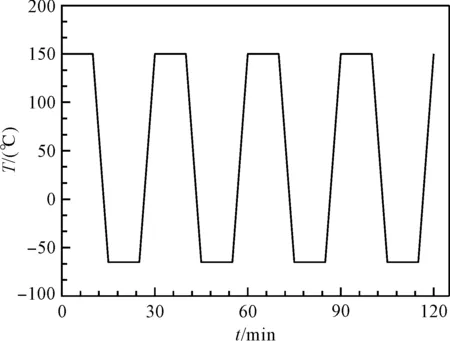
图2 温度循环实验加载示意图

2.2 实验结果讨论与分析

3种不同封装材料的功率模块在温度循环测试下的失效情况如表1所示。

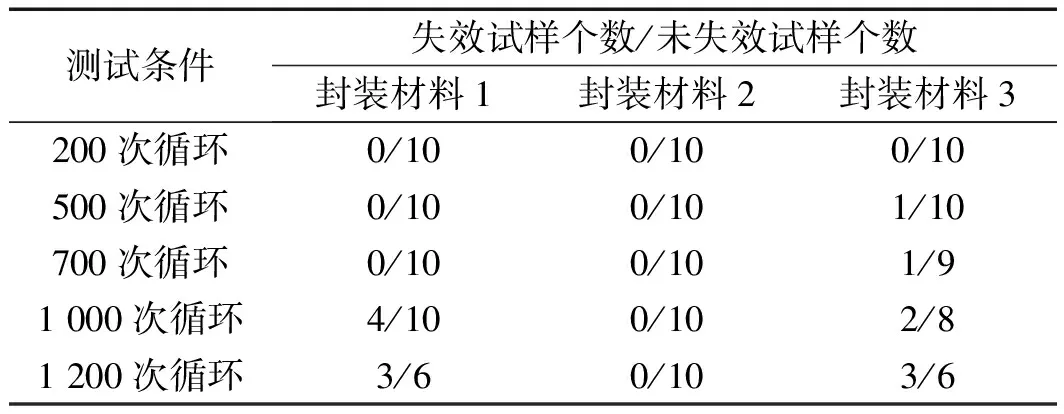
表1 实验测试的各封装材料试样的失效情况

由表1可以看出，在同样的温度循环作用下，由于封装材料的不同，各功率模块的疲劳寿命呈现出较大的差异。使用封装材料2的功率模块具有最高的疲劳寿命，封装材料1的疲劳寿命次之，封装材料3的疲劳寿命最低。

温度循环实验后，解除封装材料后的失效试样实物图以及失效试样的局部细节如图3所示。

图3 失效试样实物图及其细节

从图3中可以看出，经温度循环实验后，功率模块中多处引线键合部位发生了破坏，其失效形式主要分为两类，一种表现为引线与芯片之间的脱粘，另一种则是引线颈部的断裂。引线与芯片之间的脱粘，原因在于引线与芯片之间的热膨胀系数不匹配；而引线颈部的断裂，则是在温度循环作用下，引线颈部的应力集中造成的。

3 有限元模拟与寿命预测

3.1 有限元模型的构建

本研究基于实际的功率模块模型，利用软件Ansys建立了有限元模型，并结合子模型技术，对关键引线构建了更为真实的子模型。由于本研究的对象为引线，为适当地简化模型，在整体模型中只建立了几根典型的引线，整体模型如图4所示。

图4 功率模块有限元模型

模型中主要的材料及其参数如表2、表3所示。

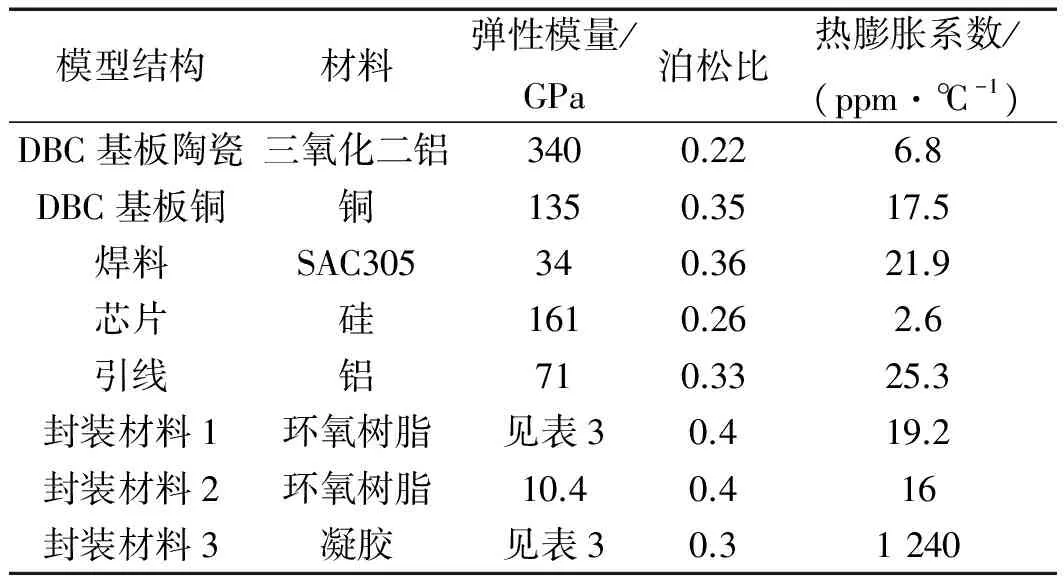
表2 功率模块材料基本特性

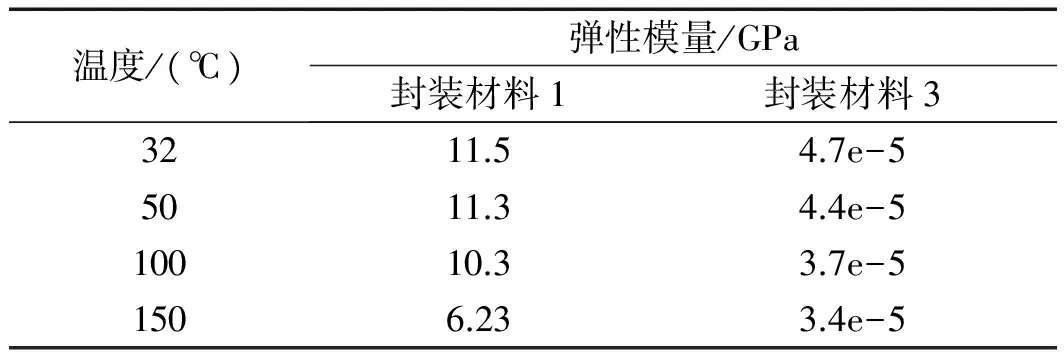
表3 封装材料温度相关特性

运用子模型方法，首先须对整体模型进行分析计算。本研究在整体模型的分析计算中，对所有节点施加如图2所示的温度循环载荷。为减少计算时间，只计算了4个循环周期。待整体模型计算完成后，对薄弱部位利用子模型技术，进行更为细致真实的建模。子模型建立后，对切割边界施加边界条件，对所有节点施加与整体模型相同的温度载荷进行计算，与整体模型一样，同样计算4个循环周期。

3.2 基于经验寿命预测方法的寿命预测

本研究通过对所有封装材料的功率模块模型进行温度循环的模拟，发现在所有情况下，引线键合部位塑性应变幅的最大值均出现在引线键合的界面处。现以封装材料2的模型为例，分析引线键合部位在温度循环载荷作用下应变情况,有限元模拟结果如图5所示。

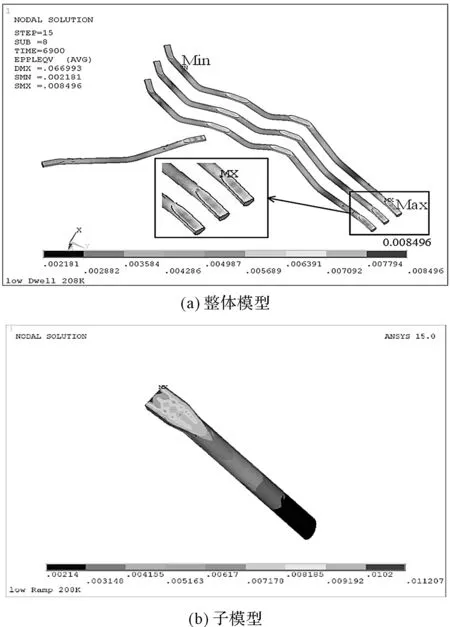
图5 有限元模拟结果

从图5中可以看出，塑性应变的最大值发生在引线键合的界面处，这与实验的结果相吻合。而由于网格划分的不规则，在靠近引线颈部的节点上发生了很大的应力集中，这是不合理的。而在子模型中，由于对引线进行了更加接近真实情况的建模，消除了网格奇异性，可以看到，与整体模型结果相同的是，塑性应变的最大值都发生在引线键合的界面处，不同的是键合界面的末端不再出现应力集中现象。因此，说明子模型的计算结果要比整体模型的计算结果更加符合真实情况。

本研究结合以上所述的有限元分析结果以及实验结果，利用式(4)的Coffin-Manson疲劳寿命预测公式进行拟合，得到两个待定参数值C1=28.38，C2=-0.695，并代入到公式中，即得到不同封装材料中功率模块引线键合处的疲劳寿命，如表4所示。

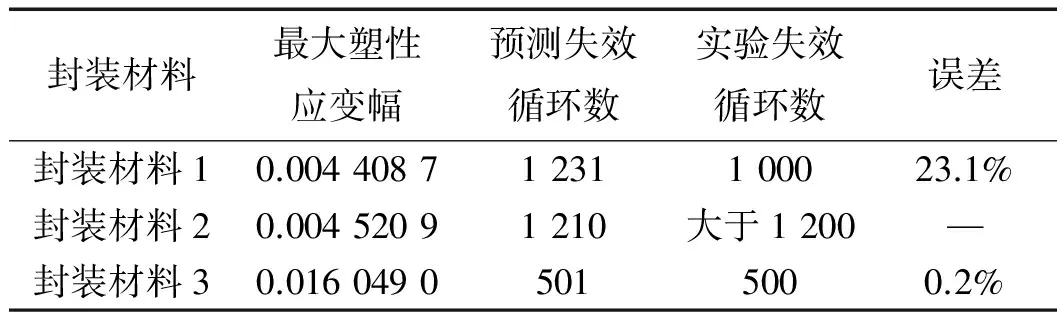
表4 基于塑性应变幅的预测疲劳寿命与实验结果

由表4可以看到：该公式对3种封装材料的疲劳寿命预测结果总体上存在一定误差。由于数值模拟结果毕竟是在理想化的条件下得出的，因此当前误差也是可以接受的。该方法基本可以用来表征不同封装材料的疲劳寿命，对实际的生产制造能够提供一定的指导。同时需要注意的是，封装材料1与封装材料2的最大塑性应变幅值非常接近，且封装材料2的应变幅值还略大于封装材料1，但两者的疲劳寿命却相差较大，甚至封装材料2的寿命还大于封装材料1，说明该公式还存在一定的局限性。

3.3 基于循环内聚力模型的寿命预测及失效分析

基于前一节中建立的子模型，在Ansys埋入内聚力单元，再逐一将Ansys中的节点单元信息，子模型边界条件等转入到Abaqus input文件中，设置合适的内聚力模型参数，并加以温度循环载荷和循环边界条件，最后调用UEL程序进行分析。根据经验，对比相关实验与数值模拟结果，综合确定内聚力参数如下：0.005 mm，0.01 mm，0.005 mm，0.01 mm，1MPa，0.02 mm，0。这7个参数分别表示内聚力模型的法向特征位移，法向断裂位移，切向特征位移，切向断裂位移，法/切向最大应力，疲劳损伤阈值，内聚力单元厚度。计算时，在UEL程序中利用UEXTERNALDB接口对计算结果进行输出，最后，在Matlab程序中结合单元连接信息，绘制界面处的损伤云图，考察界面处的损伤演化情况。

通过后处理发现：界面处各点上的法向应力均为负值，说明键合界面在温度循环的过程中，一直受到封装材料的挤压，由于在损伤计算准则中忽略了压缩的作用，可以认为在此例中，法向应力在界面的损伤失效中贡献较小，界面的失效以切应力为主导。以封装材料1的引线键合模型为例，分别经过200，400，600次循环加载后，引线键合界面处的疲劳损伤情况如图6所示。

图6 经若干次循环后封装材料1模型键合界面的损伤情况

从图6中可以看出：两侧的引线损伤累积最快，在经过600次循环后，键合界面的大部分区域已经产生了程度为0.9左右的损伤，而中间引线的损伤累积速率较低，损伤面积稍小。同时，还可以注意到的是，损伤的累积往往从界面的中间部位开始，逐渐往两边扩展，说明界面的中间部位是最容易引起损伤的薄弱部位。

将键合界面中所有内聚力单元在循环后的损伤程度Di求平均，视为界面的总体损伤程度D，得到不同封装材料中界面的损伤程度与温度循环数之间的关系，如图7所示。

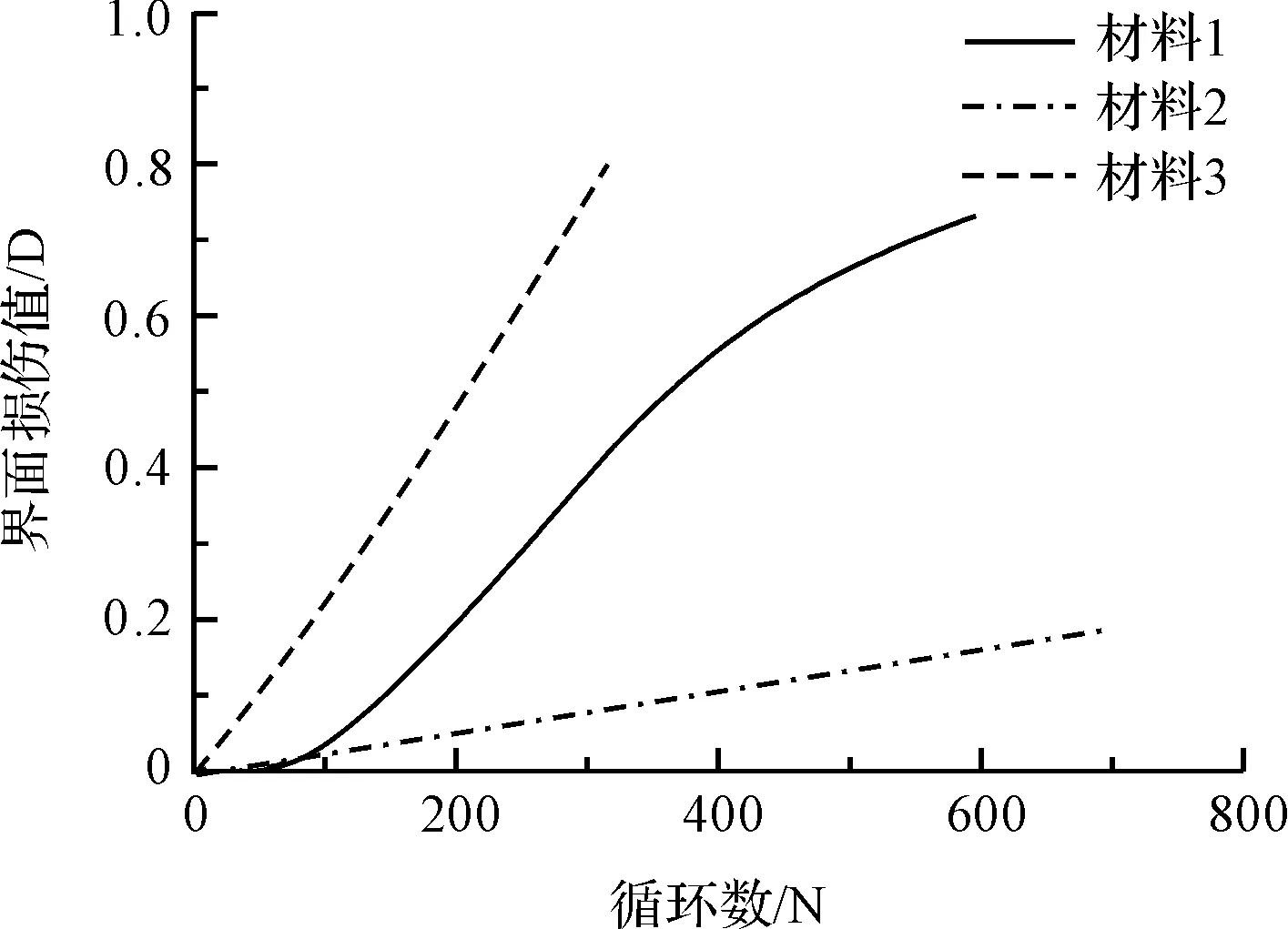
图7 键合界面损伤累积随循环数的变化

从图7中可以看出：封装材料3中界面的损伤累积速度最快，材料1次之，材料2最慢。根据3种封装材料中键合界面损伤累积的趋势，可以对其疲劳寿命进行预测，结果如表5所示。

表5 基于循环内聚力模型的预测疲劳寿命与实验结果

结果表明：封装材料2下的引线键合疲劳寿命最高，材料1次之，材料3最低，这与实验的结果相一致，同时弥补了前一节中基于塑性应变幅进行寿命预测时，不同封装材料中界面应变幅相近时，实际疲劳寿命却相差较大的不足，证明该方法具有一定的可靠性。

4 结束语

本研究分别利用传统的疲劳寿命预测方法和现有的疲劳寿命预测理论以及损伤累积理论，结合实验的方式，对功率模块引线键合界面在温度循环作用下的失效情况进行了研究。结果表明：在温度循环作用下，引线键合的界面处为最容易失效的薄弱部位，封装材料的不同对其疲劳寿命有着较大的影响。

利用Coffin-Manson公式对引线键合界面进行寿命预测，其结果具有一定的可靠性，但在两种材料中界面的塑性应变幅值较为接近的情况下，其寿命预测结果显示出一定的局限性。

[1] 刘 勇,梁利华,曲建明.微电子器件及封装的建模与仿真[M].北京:科学出版社,2010.

[2] 李 琦,徐弘毅,金 锐,等.封装键合点对IGBT UIS失效的影响研究[J].机电工程,2015,32(5):707-711.

[3] HUNG T Y, LIAO L L, WANG C C, et al. Life prediction of high-cycle fatigue in aluminum bonding wires under power cycling test[J].IEEETransactionsonDeviceandMaterialsReliability,2014,14(1):484-492.

[4] 谢鑫鹏.功率器件封装的可靠性研究[D].广州:华南理工大学电气与信息学院,2010.

[5] COFFIN L F. Fatigue at high temperature[M]. San Francisco: American Society for Testing and Materials,1973.

[6] DUGDALE D S. Yielding of steel sheets containing slits[J].JournaloftheMechanicsandPhysicsofSolids,1960,8(2):100-104.

[7] BARENBLATT G I. The mathematical theory of equilibrium cracks in brittle fracture[J].AdvancedinApplied

Mechanics,1962,7(C):55-129.

[8] HALLETT S. 13-Predicting progressive delamination via interface elements[J].JournalofCompositeMaterials,1998,32(14):1246-1272.

[9] XU X P, NEEDLEMAN A. Analysis of ductile crack growth by means of a cohesive damage model[J].InternationalJournalofFracture,1996,81(2):99-112.

[10] TVERGAARD V, HUTCHINSON J W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids[J].JournaloftheMechanicsandPhysicsofSolids,1992,40(6):1377-1397.

[11] ROE K L, SIEGMUND T. An irreversible cohesive zone model for interface fatigue crack growth simulation[J].Engineeringfracturemechanics,2003,70(2):209-232.