应用于高速永磁同步电机的改进最大转矩电流比控制研究*

袁庆庆，李龙吟，杨 娜

(上海理工大学 光电信息与计算机工程学院，上海 200093)

0 引 言

相较于普通电机而言，高转速永磁同步电机具有功率密度高、传动效率高以及低噪声的优点，广泛应用于高档数控机床、飞轮储能以及航空舰载驱动等系列工业生产领域[1]。高转速永磁同步电机的定子电感较小，在由电力电子变流器驱动供电时，上述低电感特性能保证定子电流的动态响应速度，但易受运行环境影响出现较大参数波动问题、影响系统控制效果[2-4]。

当高转速永磁同步电机应用于电动汽车等领域时，电机控制系统的设计不仅要满足实际路况要求，还需在最大程度上提高电机运行效率，因此常采用最大转矩电流比方式[5-6]。传统的MTPA控制由于受电机电感参数等干扰，存在最大转矩电流控制点计算出现偏差、计算复杂等问题。

本研究设计以内插式高转速永磁同步电机为对象，对其开展考虑电机定子电感等参数影响时的MTPA控制研究。

1 内插式永磁同步电机电磁关系

1.1 电机模型

两相旋转坐标系的内插式永磁同步电机的定子电压方程与磁链方程分别为[7]：

(1)

(2)

电磁转矩方程为：

(3)

式中：id，iq，ud，uq，ψd，ψq—电机的定子电流、定子电压和磁链在d、q轴上的分量；Ld，Lq—电机的直轴同步电感和交轴同步电感；ωe—电机电角速度，ωe=PnΩ；Pn—电机极对数；Ω—电机机械角速度；p—微分算子；Rd，Rq—电机定子d、q轴电阻；ψf—电机转子磁通。

1.2 电磁关系

实际运行中的电机定子相电流极限值imax和相电压极限值umax会受到逆变器输入电压和输出电流限制[8-11]。假设电机稳定运行，则其定子相电压满足：

(4)

将式(1)中的电压关系代入式(4)，同时忽略电阻压降，得到稳态运行时的定子电压极限最大值umax为：

(5)

同样，定子相电流的极限方程可表示为：

(6)

电机输出电磁转矩的运行轨迹，可通过对转矩表达式进行标幺值转换获取。对式(3)进行标幺值变换后的转矩标幺值为：

(7)

结合式(5-7)，电流矢量关系图如1所示。

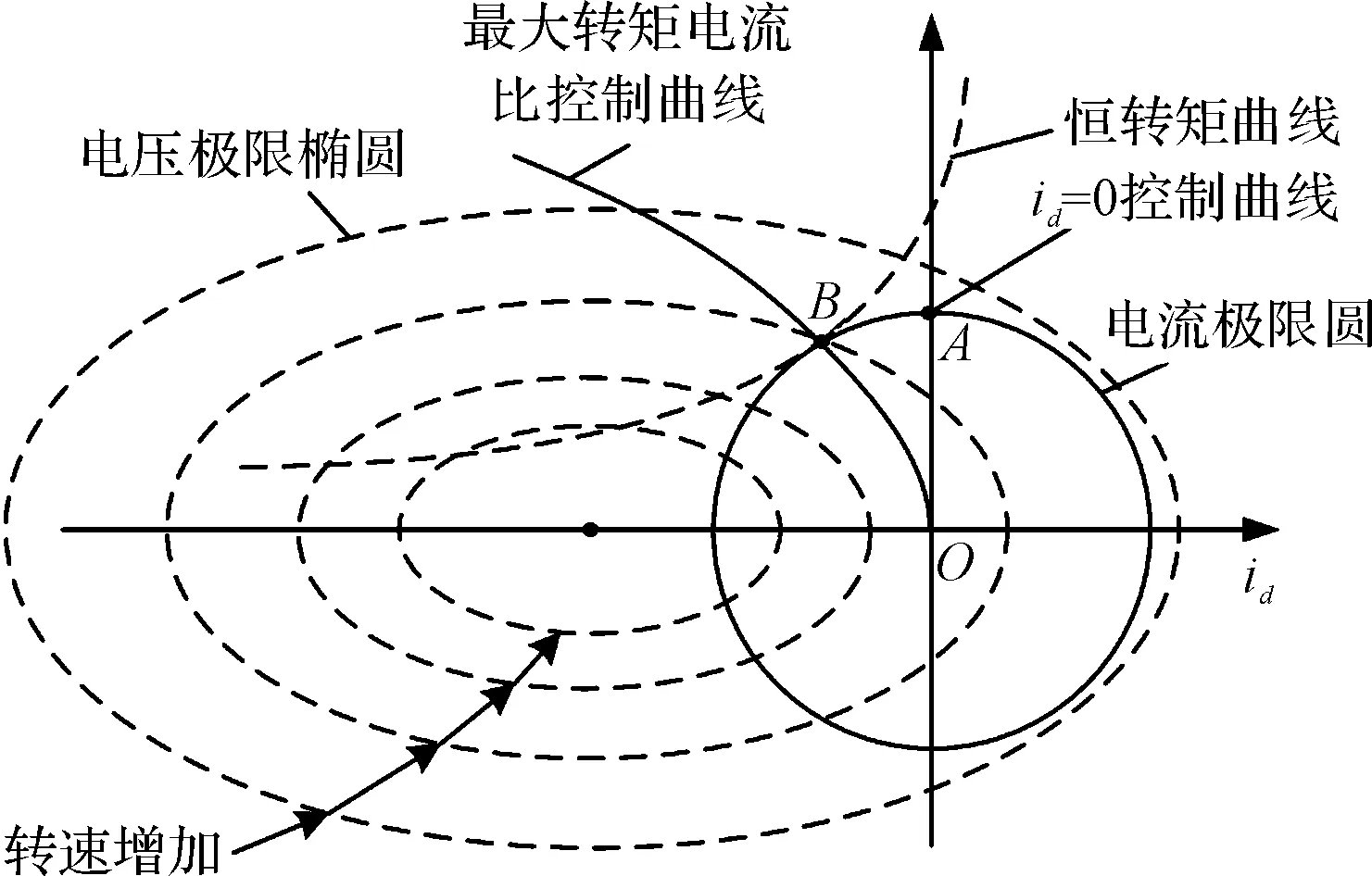
图1 矢量控制策略的电流矢量关系

其中的最大转矩电流比曲线由将恒转矩轨迹上距离原点最近的点相连接而成。

2 改进MTPA控制

2.1 传统MTPA存在问题分析

恒转矩轨迹与电流矢量关系如图2所示。

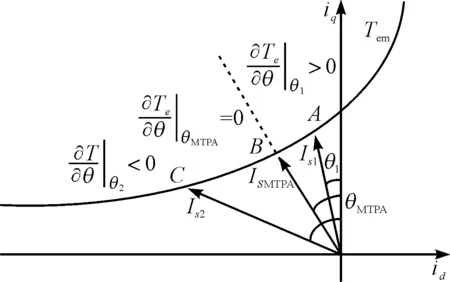
图2 恒转矩轨迹与电流矢量

同时，由图2中的转矩、电流关系将式(3)改写成如下形式：

(8)

所谓的MTPA工作点为∂Tem/∂θ=0所对应的θ点，将式(8)对角度求偏导得：

(9)

令式(9)=0，即可得到MTPA工作点为：

(10)

此时，对应的电流取值为：

(11)

由式(11)可知，求取得到θMTPA中含有d、q轴电感和磁链参数，易受实际运行环境的影响而出现较大偏差，无法满足高性能控制要求。

2.2 改进MTPA控制

2.2.1 控制思想

在图2的电流矢量角θ中注入一个高频小信号Δθ，并对其进行泰勒级数展开得到：

(12)

注入的小信号角度分量可表示为Δθ=Asin(ωht)，其中：A—较小的幅值；ωh—高频角频率。

由于注入信号的幅值较小，可忽略其对电流和转速的影响，此时在MTPA工作点附近有以下几种情况：

(1)A点，即θ<θMTPA，此时Te的变化方向同注入信号的大小变化方向一致，即∂Tem/∂θ>0。根据式(12)可知，此时由Δθ引起的电磁转矩变化主要由∂Tem/∂θ决定，且其变化频率同注入信号频率一致，变化方向也一致；

(2)B点，即θ=θMTPA，此时正好∂Tem/∂θ=0，根据式(12)可知，此时由Δθ引起的电磁转矩变化主要由二阶偏导项决定；

(3)C点，即θ<θMTPA，Te的变化方向同注入信号的大小变化方向相反，即∂Tem/∂θ<0，此时由Δθ引起的电磁转矩变化主要由∂Tem/∂θ决定，其变化频率同注入信号频率一致，但变化方向相反。

通过上述分析可知，高频信号注入提取θMTPA原理可总结为：注入高频小信号后，提取出转矩信号中的一阶偏导项，分离出正比于∂Tem/∂θ的部分，最后控制其为零，即可实现MTPA控制。

忽略漏感，电机输出电磁功率Pem可表述为：

(13)

而Pem与输出电磁转矩Tem、电机转速ωe之间的关系可表述为：

(14)

结合式(8)和式(14)可得到如下关系：

(15)

其中，id=-Issin(θ)；iq=Iscos(θ)。

由于注入信号的频率较高，在每个高频信号周期可以将ψf、Ld和Lq视为定值，可利用(ud-Rsid)/ωeiq和(uq-Rsiq)/ωe分别代替(Ld-Lq)pn和ψfpn，从而避免了电感和磁通的参数变化对MTPA工作点选取的影响，由此得到含有注入信号的电磁转矩计算式为：

(16)

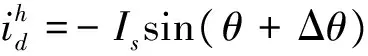
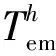
2.2.2sDFT提取

sDFT算法具体过程可表述为：

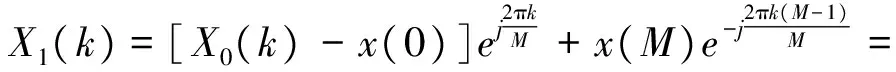
(17)

式中：x(m)—有限长序列，数据长度为M；x0—前一时刻采样点数据；x1—新的采样数据；X0(k)，X1(k)—对应的傅里叶变换值。

由式(17)可知，sDFT的整个处理过程只需要针对前一时刻采样序列傅里叶变换式进行简单的加减法和一次复数乘法即可，这种数据处理方法的运算效率要远高于FFT，非常适合使用数字处理器对高频信号进行处理。

利用sDFT算法提取k次谐波时在z域内的传递函数表达式为：

(18)

根据式(17～18)，可知sDFT的实现结构如图3所示。

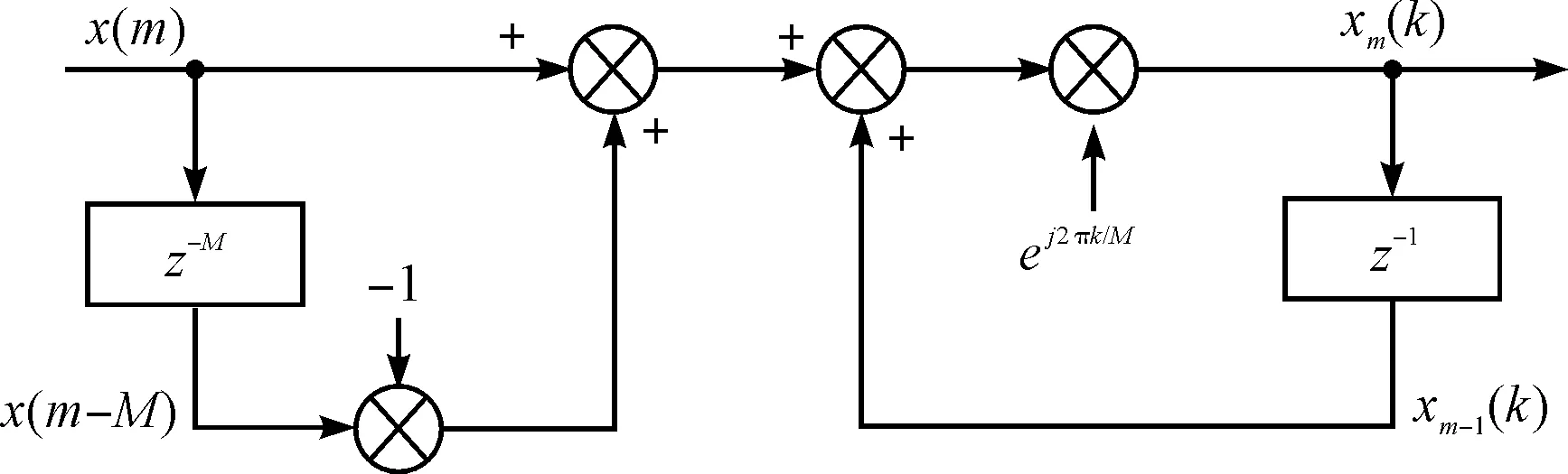
图3 sDFT的实现过程

本研究设计的基于sDFT提取包含∂Tem/∂θ的信号原理结构如图4所示。

图4 基于sDFT提取含∂Tem/∂θ部分信号原理图

(19)

式(19)的右侧包含一个直流项和一个频率为注入信号频率两倍的分量，通过一阶低通滤波器将高频项滤除，最后得到含有∂Tem/∂θ的直流项。根据前述分析，当θ≠θMTPA时，低通滤波器输出一个正比于∂Tem/∂θ的量；当θ<θMTPA时，∂Tem/∂θ=0，即低通滤波器输出为零。因此，在低通滤波器后面需加入常规积分

控制或比例积分控制器对输出信号进行调节控制，便可得到MTPA工作电流矢量角θMTPA。

3 仿真验证

基于改进MTPA控制的PMSM矢量控制框图如图5所示。

根据图5，本研究在Matlab/Simulink仿真软件中搭建相应的仿真模型，电流控制周期为200 μs，器件开关频率5 kHz；注入信号幅值为0.05，频率为500 Hz。

内插式永磁同步电机的主要参数如表1所示。

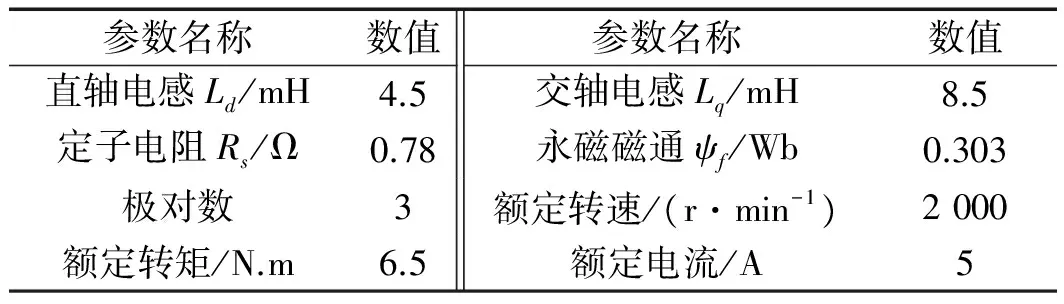
表1 内插式永磁同步电机参数

设定转速给定为100 rad/s，带载2 N·m启动，之后每经过1 s时间增加2 N·m负载，仿真时间设为3 s，得到的相应仿真结果如图6所示。

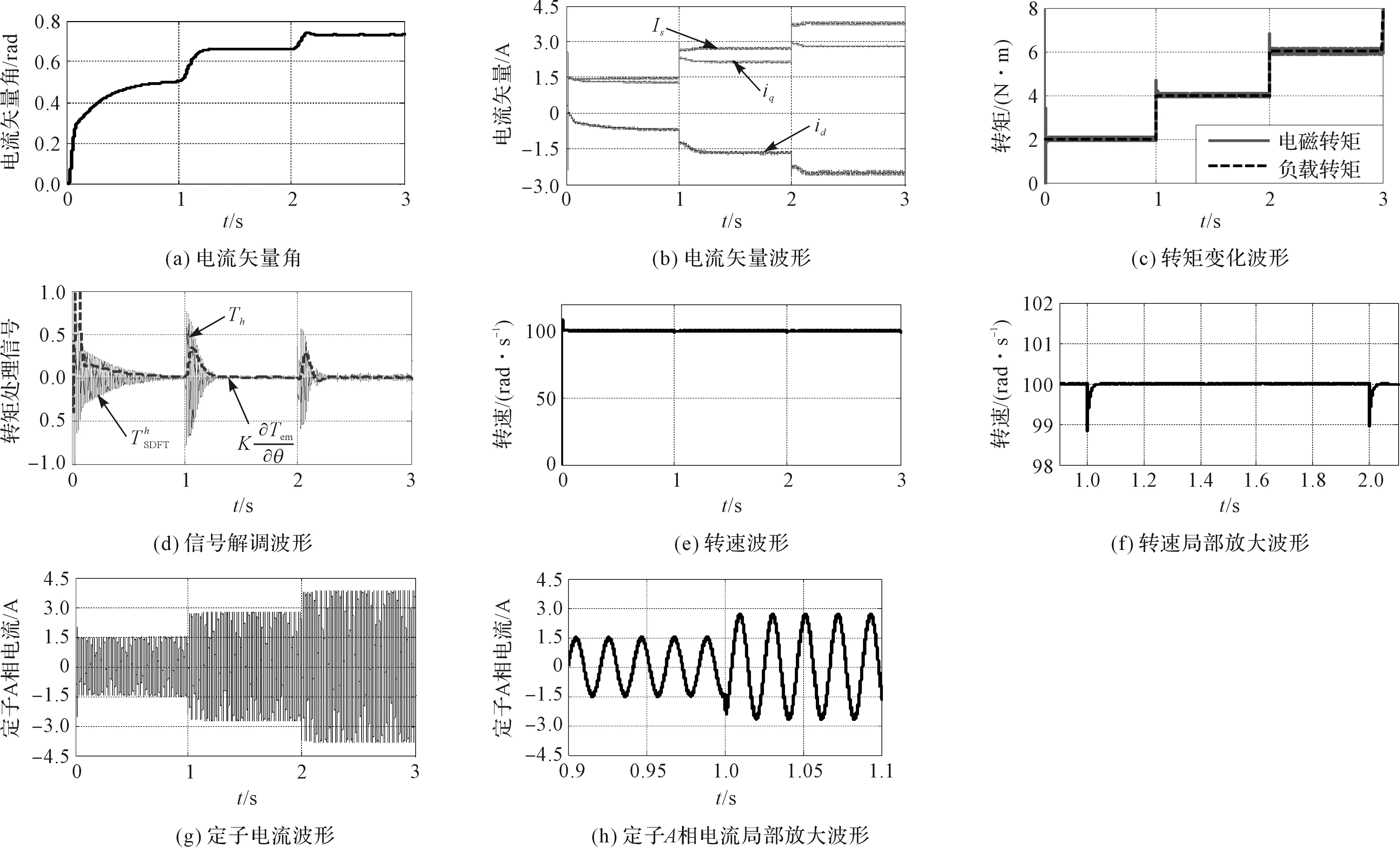
图6 改进MTPA算法的动态仿真波形

电流矢量角随负载的变化关系如图6(a)所示。在不同的负载条件下，电流矢量角都能快速的达到新的稳定值，即达到对应转矩下的MTPA工作点，电流矢量角的增大实质作用是增加id分量比重，使id、iq合成电流矢量Is达到最小。

电流矢量的整体波形如图6(b)所示。其中id为负值，且随着负载增大而幅值增加，即充分利用磁阻转矩和电磁转矩的组合，较之仅由iq提供转矩电流的id=0控制要更加有效地利用定子电流，同时也验证了该法能够实现MTPA控制。

输出电磁转矩波形如图6(c)所示。

sDFT提取一节偏导值波形如图6(d)所示。

系统转速响应波形及其局部放大图如图6(e～f)所示。从中可以看出：转速控制响应快，稳态无静差，且在每个负载突增时刻，转速掉落小，调节时间短，验证了该控制结构调速性能良好。

定子A相电流波形及其局部放大图如图6(g～h)所示。可以看出：电流在负载转矩变化时，经过不到一个电流周期就可以达到新的稳定状态。

以上仿真结果验证了基于sDFT解调注入信号的MTPA控制方法的可行性和有效性。同时也说明了MTPA控制较之id=0控制能提高电机运行效率。

4 结束语

本研究针对内插式永磁同步电机常规MTPA控制易受电机电感等参数干扰的问题，提出了一种基于高频小信号电流矢量角注入的改进MTPA控制，首先，对注入高频小信号角度的输出电磁转矩进行泰勒公式展开，然后基于离散滑动傅里叶计算实现了MTPA控制角的有效提取。通过建模仿真对结果进行验证，实验结果表明：此改进算法可以在电机电感等参数的扰动下具有良好的抗扰性能，从而实现电机的有效控制，提高电机运行效率。

在下一阶段，本研究将改进MTPA控制与电机弱磁升速控制相结合，进一步拓宽永磁同步电机的调速范围。

[1] 李雪恺，陈 勇，张 彬，等.自适应滑模观测器的永磁同步电机无位置传感器控制[J].兵工自动化，2016，35(9)：73-77.

[2] IWASAKI M, SEKI K, MAEDA Y. High-precision motion control techniques: a promising approach to improving motion performance[J].IEEEIndustrialElectronicsMagazine,2012,6(1):32-40.

[3] 莫会成,闵 琳.现代高性能永磁交流伺服系统综述[J].电工技术学报,2015,30(6):10-21.

[4] 杨 娜,袁庆庆,宋 斌.基于Matlab和LabVIEW的永磁同步电机控制系统设计[J].机电工程,2017,34(3):2-4.

[5] 金宁治,王旭东,李文娟.电动汽车PMSM MTPA控制系统滑模速度控制[J].电机与控制学报,2011,15(8):52-58.

[6] 尹 霞.基于高频信号注入的永磁同步电动机MTPA优化[J].微特电机,2015,43(5):4-8.

[7] 李 宏,张 勇,王晓娟，等.永磁同步电机SVPWM控制策略仿真研究[J].微电机,2009,42(1):86-88.

[8] 刘 微.永磁同步电机弱磁控制策略研究[D].北京：北京交通大学机械与电子控制工程学院,2014.

[9] 毛亮亮,王旭东.一种新颖的分段式优化最大转矩电流算法[J].中国电机工程学报,2016,36(5):1404-1412.

[10] 谭建明，刘 华，张治平.永磁同步变频离心式冷水机组的研制及性能分析[J].流体机械，2015(7)：82-87.

[11] 于慎波，殷 维，钟双双.永磁同步电主轴电磁振动研究[J].机械，2015(4)：5-8.

[12] JACOBSEN E, LYONS R. An update to the sliding DFT[J].IEEESignalProcessingMagazine,2004,21(1):110-111.