基于输入时延的线性连续时不变系统量化分析与控制*

陈 俊，陈海飞，高金凤

(浙江理工大学 机械与自动控制学院，浙江 杭州 310018)

0 引 言

网络控制系统是一种将空间分布的多个系统元件如：传感器、执行器、控制器等控制节点通过数字通信网络连接的闭环反馈控制系统[1]。由于控制系统回路中通信网络的介入，不可避免地将网络其本身带宽有限等特性引入到控制系统中，必须设计出先进的控制策略。

针对时延和丢包控制问题，LI等[2]提出了一种改进的依赖时延上界和丢包上界的稳定性判据；XIE等[3]将通信受限的NCSs建模成具有输入时延的离散时间切换系统，通过求解一组线性矩阵不等式(LMIs)获得了系统的稳定性条件；ZHANG等[4]基于Markov建模方法，将传感器到控制器和控制器到执行器的两段传输时延分别建模成两个Markov链，并分析了闭环系统的随机稳定性。与此同时，Zhang等[5]考虑了一类时变时延小于一个采样周期的NCSs，进而将系统描述成离散时间切换系统，设计了相应的H∞控制器使系统达到指数均方稳定和指定的H∞性能，并建立了时延长度，时延变化频率和闭环系统性能的关系。

另一方面，在接收端恢复出信号与原信号有一定的误差。早期ELIA等[6]指出在单输入单输出的离散线性时不变系统中，对数量化器是最粗糙的量化器，得到了系统稳定的最小量化密度跟系统自身的不稳定极点有关、QU等[7]研究了离散线性无线网络控制系统的稳定性，基于Markov跳变系统，将系统稳定性转化为一个等价的不确定系统的鲁棒稳定性问题；JIANG等[8]同时考虑了网络诱导时延，数据包任意丢失，量化的影响，基于已知的丢包概率，时延的上下界和量化密度，设计了统一的控制率。以上文献都是考虑了传感器对被控对象采样的状态信息传输到控制器端的量化情况，而在实际系统中，控制器的输出信号在送到执行器端前也同样需要量化。

本研究将对系统建模、稳定性分析及控制器设计3个方面进行研究。

1 系统建模

考虑被控对象为线性时不变系统，其状态方程如下：

(1)

式中：x(t)—被控系统的状态向量x(t)∈Rn；u(t)—控制输入，u(t)∈Rp；y(t)—被控输出，y(t)∈Rr；A,B,C—具有适当维数的常数矩阵。

具有时延和量化的网络控制系统的结构如图1所示。

图1 具有时延和量化的网络控制系统的结构

为了不失一般性，对NCSs作如下假设：

假设1：网络时延在两个通道中都存在，用u(t+)=Κx(t-τsc(k))表示传感器到控制器时延，用u(t+)=Κx(t-τsc(k))表示控制器到执行器时延，两部分的总时延用u(t+)=Κx(t-τsc(k))表示，即u(t+)=Κx(t-τsc(k))。u(t+)=Κx(t-τsc(k))是有界的，即ηm≤τ(k)≤ηM,u(t+)=Κx(t-τsc(k))。

假设2：数据在每个采样周期内以单包的形式传输。传感器是时钟驱动，而控制器和执行器都是事件驱动。

假定被控系统的状态都是可观测的，则可以使用闭环状态反馈控制器:

u(t+)=Κx(t-τsc(k))，k=1,2,…

(2)

式中：Κ—状态反馈增益。

由于通信网络中存在网络诱导时延和数据包丢失的问题，将式(2)代入式(1)中得到：

(3)

式中：t∈[ikh+τ(k),ik+1h+τ(k+1)]；h—采样周期；x(ikh)—系统状态x(t)在采样时刻ikh经传感器检测出的信号。

由于零阶保持器(ZOH)的工作机制[9]，u(ikh)在采样时刻ikh总是接收最新的控制信号以保证系统的实时性，又因为x(ikh)=x(t-(t-ikh))，令η(t)=t-ikh，其中，t∈[ikh+τ(k),ik+1h+τ(k+1)]，根据假设1可知，ηm≤(ik+1h-ikh)+τ(k+1)≤ηM，所以η(t)也是有界的，即ηm≤η(t)≤ηM。结合式(1～3)，并用t-η(t)代替ikh，于是式(3)可以表示为：

(4)

其中：t∈[ikh+τ(k),ik+1h+τ(k+1)]，ηm≤η(t)≤ηM。

考虑到前馈通道和反馈通道分别加入量化器后，量化器g(·)和f(·)分别量化状态信号和控制信号，量化器与其两端的输入输出关系描述如下：

v(t)=Κg(x(ikh))

(5)

u(t)=f(v(t))

(6)

量化器f(·)和g(·)定义为：

f(v)=[f1(v1),f2(v2),…,fp(vp)]T

(7)

g(x)=[g1(x1),g2(x2),…,gn(xn)]T

(8)

其中：fi(·)和gj(·)(i=1,2,…,p;j=1,2,…,n)是对称的，即fi(-vi)=-fi(vi)和gj(-xj)=-gj(xj)，本文选取fi(·)和gj(·)为对数量化器。

定义1[10]：一个量化器被称为对数量化器，它的量化级数的集合为：

U={±ui：ui=ρiu0,i=±1,±2,…}∪
{±u0}∪{0},0<ρ<1,u0>0

(9)

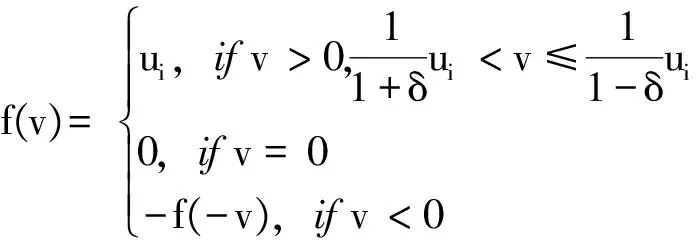
定义为：

(10)

其中：

(11)

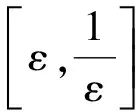
(12)

利用扇形界方法可将fi(·)和gj(·)表示为[11]：

fi(vi)=(1+Δfi(vi))vi，|Δfi(vi)|≤δfi

(13)

gj(xj)=(1+Δgj(xj))xj，|Δgj(xj)|≤δgj

(14)

于是量化器fi(·)和gj(·)可以表示为：

f(v)=(Ι+Δf)v

(15)

g(x)=(Ι+Δg)x

(16)

其中：令Δf=Δfi，Δg=Δgj，Ι为适当维数的单位阵。根据式(1～4，15-16)得到系统的控制输入为：

u(t)=(Ι+Δf)Κ(Ι+Δg)x(ikh)=
(Κ+Δ(Κ))x(ikh)

(17)

其中，Δ(Κ)=ΔfΚ+ΚΔg+ΔfΚΔg。结合式(4)和式(17)得到：

(18)

其中：t∈[ikh+τ(k),ik+1h+τ(k+1)]。

(19)

引理2[12]：对于给定的具有适当维数的矩阵Ω1，Ω2和Ψ，σ(t)是关于t的函数，且满足0≤σm≤σ(t)≤σM，则：(σ(t)-σm)Ω1+(σM-σ(t))Ω2+Ψ<0成立当且仅当：(σM-σm)Ω1+Ψ<0，(σM-σm)Ω2+Ψ<0。

引理3[13]：对于给定的适当维数的实矩阵D，E和F且满足‖F‖≤1，则对任意给定的变量ε>0，有下面的不等式成立：

DEF+ETFTDT≤ε-1DDT+εETE

(20)

2 稳定性分析

定理1给出了其渐近稳定的一个判据，为接下来的控制器设计提供了理论基础。

定理1：给定状态反馈增益矩阵Κ和标量常数ηm，ηM，如果存在适当维数的对称正定矩阵P>0，Ti>0，Mi>0(i=1,2)和普通矩阵S，N满足式(21～22)，则闭环控制系统(18)是渐近稳定的。

(21)

(22)

其中：

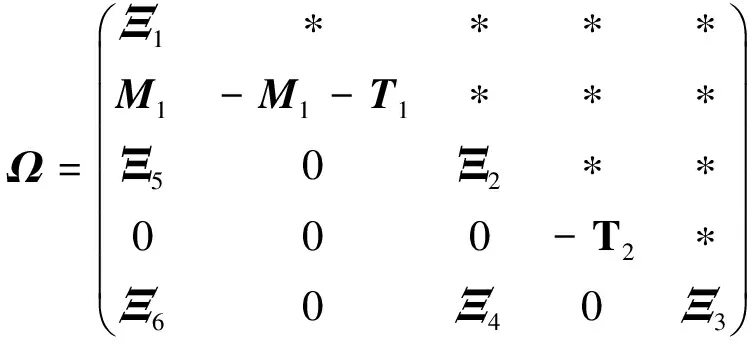
证明：选取的Lyapunov-Krasovskii泛函形式：

V(t)=V1(t)+V2(t)+V3(t)

其中：

V1(t)=xT(t)Px(t)

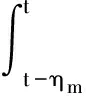
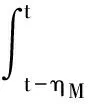
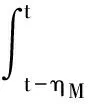
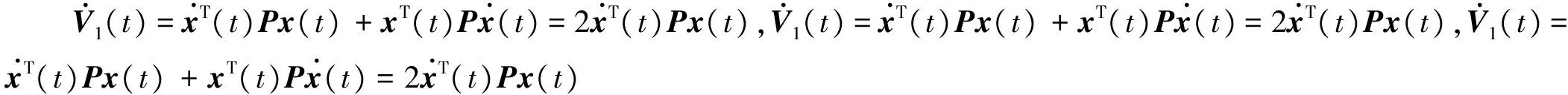
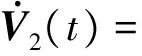
xT(t)T2x(t)-xT(t-ηM)T2x(t-ηM)

2φT(t)S[x(t-ηm)-x(t-η(t))-

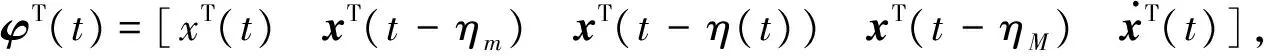
(23)

另外，其中两项：

(24)

(25)

结合式(23～25)可得：

xT(t-ηm)T1x(t-ηm)-

(x(t)-x(t-ηm))TM1(x(t)-x(t-ηm))-

2φT(t)S(x(t-ηm)-x(t-η(t)))+

2φT(t)N(x(t-η(t))-x(t-ηM))+

(26)

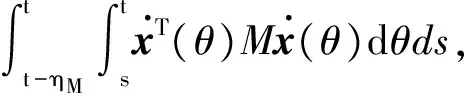
由于Δ(Κ)=ΔfΚ+ΚΔg+ΔfΚΔg是以非线性的形式存在的，其中的Δf和Δg为两个不确定项，Δ(K)也是不确定的，无法直接用Matlab中的LMI工具箱求解，所以本研究应用常见处理不确定项的方法，将其转化成如下形式。定理2给出了处理不确定项Δ(K)的具体过程。

定理2：给定反馈增益矩阵Κ和标量常数ηm，ηM，如果存在适当维数的对称正定矩阵P>0，Ti>0，Mi>0(i=1,2)和普通矩阵S，N以及变量εk(k=1,2,3)满足式(27～28)则闭环控制系统(18)是渐近稳定的。

(27)

(28)

其中：

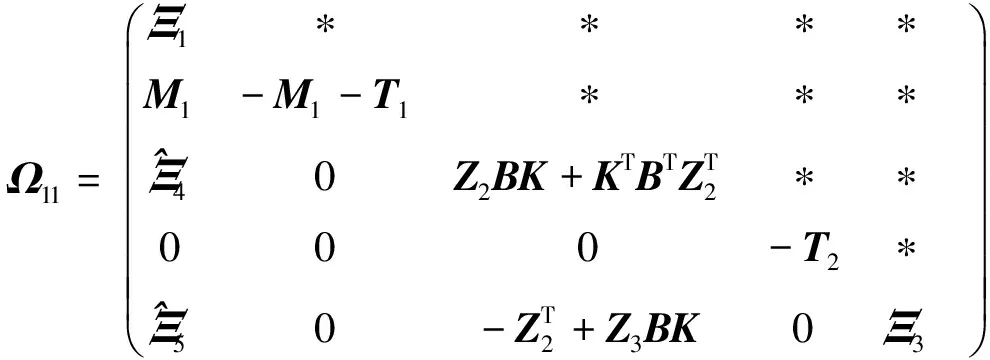
证明：将定理1中的Ω作如下形式改写：

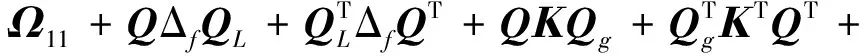
(29)

应用引理3可知，存在εk(k=1,2,3)使得下列不等式成立：

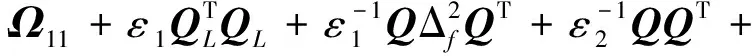
(30)

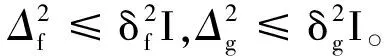
3 控制器设计

根据定理1和定理2，设计状态反馈控制器使得闭环系统(18)渐近稳定。下面给出量化反馈控制器的设计方法。

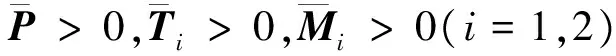
(29)

(30)

其中：

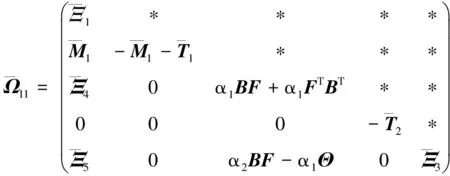
证毕。

注释2：从定理3中可以看出线性矩阵不等式(29～30)的可行性解不仅与网络诱导时延的上下界ηM，ηm有关，还与两个量化器的量化参数δf，δg有关，根据式(11)可知，两个量化器的量化密度ρf，ρg的大小直接影响线性矩阵不等式(31～32)的求解。

4 数值仿真示例

例1：考虑如下线性系统：

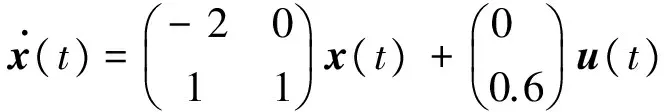
同时选取两个量化器为对数量化器，并选择适当的量化密度，根据定理3，取常数α1=9.6，α2=8.0，对应有不同的量化密度ρf和ρg。

在不同的量化密度下，系统的相关参数如表1所示。

表1 不同量化密度下系统的相关参数比较

3种量化密度下系统的状态响应如图3所示。

图3 3种量化密度下系统的状态响应

从图3可以看出：(1)通过量化反馈控制器可以使系统渐近稳定；(2)随着量化器的量化密度增大，量化器对信号的采样和量化越精细，对系统的信息了解越多，系统到达稳定状态的时间变短，则系统的控制性能变好。

5 结束语

本研究运用Lyapunov稳定性理论提出了一种基于时变时延依赖的Lyapunov-Krasovskii泛函，并得到了以两个线性矩阵不等式(LMIs)表示的稳定性判据；在不考虑外部干扰的情况下，设计了量化状态反馈控制器使得系统渐近稳定，并且得到系统的控制性能与量化器的量化密度ρf和ρg密切相关；最后给出的数值仿真示例验证了所提方法的有效性。

[1] 游科友，谢立华.网络控制系统的最新研究综述[J].自动化学报，2013，39(2)：101-118.

[2] LI H B, YANG H J, SUN F C, et al. A network-bound-dependent stabilization method of networked control systems[J].Automatica,2013,49(8):2561-2566.

[3] XIE D, CHEN X, LV L, et al. Asymptotical stabilisability of networked control systems: time-delay switched system approach[J].IETControlTheoryandApplications,2008,2(9):743-751.

[4] ZHANG L Q, SHI Y, CHEN T W, et al. A new method for stabilization of networked control systems with random delays[J].IEEETransactionsonAutomaticControl,2005,50(8):1177-1181.

[5] ZHANG W A, YU L, YIN S. A switched system approach to H∞control of networked control systems with time-varying delays[J].JournaloftheFranklinInstitute,2011,348(2):165-178.

[6] ELIA N, MITTER K. Stabilization of linear systems with limited information[J].IEEETransactionsonAutomaticControl,2001,46(9):1384-1400.

[7] QU F L, HU B, GUAN Z H, et al. Quantized stabilization of wireless networked control systems with packet losses[J].ISATransactions,2016,6(4):92-97.

[8] JIANG S, FANG H J. Quantized stabilization of discrete-time systems in a networked environment[J].AppliedMathematicalModelling,2014,38(5-6):1685-1697.

[9] FENG Yu, CHEN Xiang, GU Guo-xiang. Quantized feedback stabilizing control for multiple-input networked systems with multiplicative random noises: a stochastic approach[C]. American Control Conference, Portland: IEEE,2014.

[10] LI F W, SHI P, WANG X C, et al. Fault detection for networked control systems with quantization and Markovian packet dropouts[J].SignalProcessing,2015,111(C):106-112.

[11] LIU T F, JIANG Z P, HILL D J. A sector bound approach to feedback control of nonlinear systems with state quantization[J].Automatica,2012,48(1):145-152.

[12] HAN Qing-long. Absolute stability of time-delay systems with sector-bounded nonlinearity[J].Automatica,2005,41(12):2171-2176.

[13] CAO Y Y, SUN Y X, JAMES L. Delay-dependent robust H∞control for uncertain systems with time-varying delays[J].IEEEProceedings-ControlTheoryandApplications,1998,145(3):338-344.

[14] FU M Y, XIE L H. The sector bound approach to quantized feedback control[J].IEEETransactionsonAutomaticControl,2005,50(11):1698-1711.