基于试验台架对齿轮齿条转向器的转向梯形设计与校核
2018-01-24李世豪
李世豪
(长安大学汽车学院,陕西 西安 710064)
引言
齿轮齿条式转向器目前为止在轿车以及轻型货车上应用最广泛的一种转向器,相比于其他类型的转向器,齿轮齿条式转向器构造简单、安装方便、操作轻便、效率高达90%,因此得到了广泛的应用。相对于另一应用广泛的循环球式转向器,齿轮齿条式转向器的齿条与汽车的前轴平行,通过梯形臂和横拉杆与前后左右车轮连接,从而构成了比较特殊的转向梯形。
根据悬架的类型,转向梯形分为两类:整体式与断开式。随着汽车工业的不断进步与发展,目前轿车都采用(麦弗逊)独立悬架,与之对应的就采用断开式转向梯形。与四杆式(整体式)转向梯形相比,六杆式(断开式)转向梯形的结构更加复杂,运动更加多变。
1 转向梯形的理论特性
汽车在转弯过程当中为了满足驾驶员的转向需求,其左右前轮的转角并不相同,而是内轮的转角大于外轮的转角,只有这样,才能使前、后轴相交的一点,保证两车轮具有同一个滚动中心,从而使得两车轮绕其做纯滚动。若车轮为纯滚动,它们的运动就会逐渐相互靠近,然而车轮安装在同一轴的两端,轮距B不变,因此会使得车轮在转向过程中产生边滚边滑的现象,从而使得行驶阻力增加,转向困难,轮胎磨损严重。所以在实际中将转向机构设计成梯形,当汽车转向时,前外轮和前内轮就会产生不同的转向角,从而实现车轮的纯滚动。
如图1所示,为汽车右转弯过程的车轮转角情况简图。由三角函数计算可得内外转向车轮的转角关系,既Ackerman公式:

图1 理论的转向特性曲线
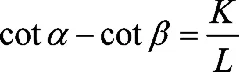

K为两主销延长线到地面交点间的距离,基本等于前轮轮距[1];
L为主销延长线与地面交点到后轴的距离[1]。在图1中,GC线为理论上的转角正确的转向梯形特性曲线,其证明如下:
在GC线上任取一点E与A和B点相连,过E点做垂直于前轴的垂线EF,则在△AEF和△BEF中

由此可见,GC线上任何一点与A和B两点的连线所形成的α角和β角都符合纯滚动的关系。所+以称GC线为理论特性曲线,有了这条线,就可以很方便的对转向梯形进行设计校核[2]。
在对转向梯形进行设计时,应当保证内、外轮转角符合或近似纯滚动关系式,即内、外转向轴线的交点都应在 GC线上或者其附近。

即在理论情况下,内转向轮转角β相对于外转向轮转角α的函数关系式[3]。
2 转向梯形的实际特性
如图2所示,为与齿轮齿条式转向器相配合的转向梯形机构简图。和传统的整体式转向梯形相比,转向横拉杆被断开,转向梯形机构由四杆机构变为六杆机构。和一般的断开式转向梯形相比,齿轮齿条式转向器的转向梯形机构也比较特殊[4]。在齿轮齿条式转向器的转向梯形中,齿条3的作用相当于横拉杆,齿条3左右两端分别通过球接头与左右横拉杆4相连,左右横拉杆4再通过球接头连接左右梯形臂5,从而形成六杆转向梯形机构。在图2所示的转向机构中,齿条3只能做横向运动,这是与一般断开式转向梯形机构的最大不同之处。

图2 齿轮齿条式转向梯形机构
以汽车左转弯为例,则左转向轮为内轮,右转向轮为外轮。
在转向过程中,右转向轮(外轮)的各杆运动情况如图3所示。

图3 外轮各杆运动情况
通过计算可得,齿条行程S与外轮转角α的关系是:
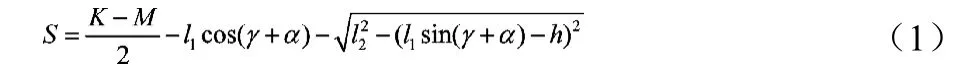
由三角函数可得:

同理,在转向过程中,左转向轮(内轮)的各杆运动情况如图4所示。

图4 内轮各杆运动情况
同理,由计算可得,齿条行程S与内轮转角β的关系为:

将式(1)代入到式(4)中,即可以得到在实际情况下,内转向轮转角β相对于外转向轮转角α的函数,即β=F(α)。同理也可以得到外轮转角α相对于内轮转角β的函数。
3 转向梯形的校核
由上述的理论内外轮转角函数和实际内外轮转角函数可得,在转向过程中,内、外车轮在转向过程中的实际运动轨迹与理论运动轨迹不同,即实际特性曲线与理论特性曲线不同。在图1中,GC线为理论特性曲线。
以某款大众轿车的相关参数为例:
梯形臂长:l1=120mm横拉杆长:l2=420mm齿条长度:M=490mm
齿条到前轴距离:h=145mm梯形底角:γ=70°主销间距:K=1480mm
将以上各参数代入β=F(α)中,即可得到实际内、外轮的转角关系函数。由于采用计算的方程式较复杂,故可以运用试验的方法对其转向梯形进行校核。
为了验证实际的内、外转向车轮的转角关系与理论上的区别,可以将大众轿车安装在实验台架上,来测量转向轮的转角,采用试验的方法来验证。
如图5所示,首先用锁销将红色滑盘固定,使其零刻度线对准指针,再将转向车轮置于红色滑盘的中心位置。转动转向盘使其回正,此时转向轮不转动任何角度。拔下滑盘锁销,转动转向盘使车轮向右转动,根据滑盘上的角度,使右轮(内轮)分别转 5°、10°、15°······,同时记录左轮(外轮)所转过的角度 α1、α2、α3······,如表 1 所示

表1 内轮转角β与外轮转角α的关系
根据内、外转向轮的对应转角关系,可以得到转向梯形的实际特性曲线,如图6所示。其中,红色的线代表实际的转向梯形特性曲线,GC直线代表理论特性曲线。同理,将表1数据和Ackerman公式输入MATLAB软件中,可得到如图7所示的转向梯形曲线。通过CAD软件和MATLAB软件仿真即可对转向梯形进行精确校核。由于实际与理想存在差异,所以两条线不重合。在设计过程中,应当使实际特性曲线尽可能的靠近理论特性曲线(GC线),从而满足转向要求[2]。

图5 内外轮转角关系实验

图6 转向梯形特性曲线
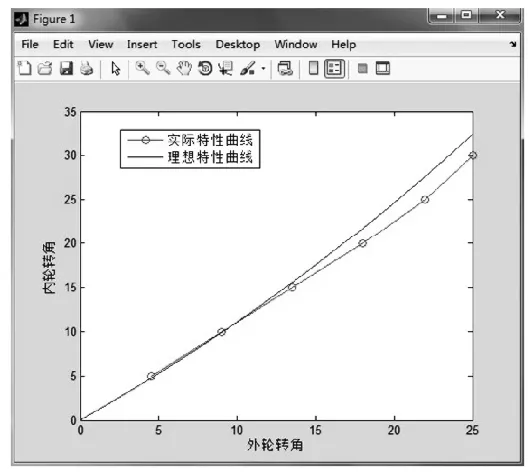
图7 转向梯形的函数曲线
4 结论
通过选取不同的梯形臂长 l1、横拉杆长 l2、齿条到前轴距离 h、梯形底角γ等相关参数,可以绘制出不同的实际转向梯形曲线。在所有的转向梯形曲线中,选取一条最接近理想特性曲线的那条曲线作为最终的特性曲线。其所对应的转向梯形关参数即为最佳值。
[1] 刘惟信.汽车设计[M].北京:清华大学出版社,2001:608-666.
[2] 李霄锋.汽车底盘设计[M].北京:清华大学出版社,2010:338-401.
[3] 王望予.汽车设计[M].北京:机械工业出版社,2004:219-256.
[4] 孙桓,陈作摸,葛文杰.机械原理[M].北京:高等教育出版社,2013:195-235.
[5] 濮良贵,陈国定,吴立言.机械设计[M].北京:高等教育出版社,2013:186-223.
