找好铺垫使学生的思维升级

黄伟 王宗信

【关键词】命题技巧；初中数学；两点距离

【中图分类号】G633.6 【文献标志码】A 【文章编号】1005-6009（2018）91-0063-02

【作者简介】1.黄伟，江苏省江阴市西石桥中学（江苏江阴，214441）教师，一级教师；2.王宗信，江苏省徐州爱登堡国际学校（江苏徐州，221000）副校长，正高级教师，江苏省特级教师。

数学试题的命制不能一味以难为准，命题除了考查学生对学科知识和能力的掌握外，还要利于学生学科素养的形成。为此，我们可以在命题中加上一些铺垫，逐步使学生的思维升级。现以“两点距离”型试题的命制为例，说明具体的做法。

例1：如图1-1，Rt△ABC中，∠ACB=90°，△ACD是等边三角形，DF⊥AC、垂足为F、与AB相交于點E，连接CE。

（1）证明：△AED≌△CED；

（2）P是直线DE上的一点（图1-2），连接PB、PC。

①求证：PA=PC；

②若AB=10，PB+PC是否有最小值，若有求出此时PB+PC的值，若没有请说明理由。

适用范围：在八年级上学期学生初学全等三角形、轴对称图形后，结合七年级所学的“三角形的两边之和大于第三边”以及“两点之间线段最短”，就可以在月考、期中考试使用这个系列的题组进行训练、考试。

命制思路：首先是考查学生对于等边三角形的轴对称性掌握情况，试题中“△ACD是等边三角形，DF⊥AC、垂足为F ”考查了等腰三角形底边上的三线合一，可以得到直线DF是线段AC的垂直平分线，再根据垂直平分线的性质“垂直平分线上的点到线段两端的距离相等”，易证△AED≌△CED，此处考查了学生全等三角形判定的学习情况。

直线DF是本题一条关键的直线，它贯通整个图形，它是对称轴，有了问题（1）的解决，问题（2）的求证只需利用垂直平分的性质便迎刃而解，同时也为解决最后一个问题起到了一个很好的铺垫。

利用前一问题中得到的结论，等量代换PB+PC=PB+PA，P是动点，如图1-3当A、P、B三点不共线时，△APB中有PB+PA>AB（三角形的两边之和大于第三边），而A、B两点是定点，PB+PA就转化为两定点间连线的长，其长度何时最短可以根据基本事实“两点间线段最短”来解决，当且仅当A、P、B三点共线时（即P为直线DF与线段AB的交点时），PB+PA=AB，结合上述两种情况的探究可以得到PB+PA≥AB。

在解决本题的过程中，需要考查学生灵活运用轴对称的性质，在变化的过程中寻找到那些不变的关系，巧妙实现直线（对称轴）同侧的两条线段之和转化为对称轴异侧两定点之间连线线段最短的转化，有助于积累数学活动经验，发展空间观念。本题的命制体现了对学生认知的尊重，以人为本，遵循呈现低起点、易进难出、渐入佳境的原则。

上题是利用轴对称性作一次对称点，利用对应线段相等，把在对称轴同侧的两点距离转化为“对称轴异侧两点间线段最短”解决问题，有的时候，一次对称不能完成任务，需要两次对称，如例2。

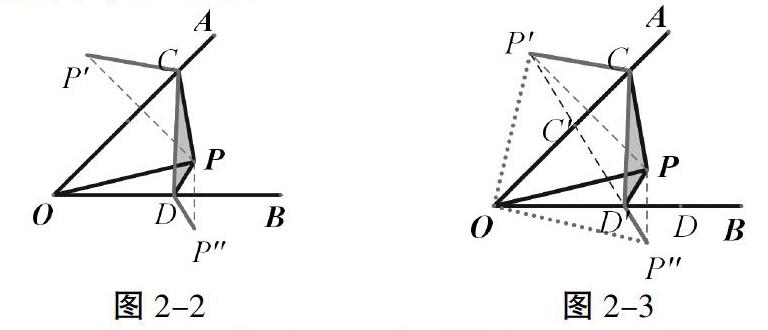
例2：已知∠AOB，P为其内部一点，OP=6，C、D分别为OA、OB边上的一动点，要使△PCD的周长最小，请给出确定点C、D位置的方法，并求出最小周长。

（1）如图2-1，若∠AOB=45°，其他条件不变，要使△PCD的周长最小，请给出确定点C、D位置的方法，并求出最小周长。

（2）若∠AOB=30°，其他条件不变，要使△PCD的周长最小，请给出确定点C、D位置的方法，并求出最小周长。当∠AOB=60°时，又如何呢？

适用范围：在八年级上学期学生初学全等三角形、轴对称图形，特别是等腰三角形的性质之后，结合七年级所学的“三角形的两边之和大于第三边”以及“两点之间线段最短”，就可以在月考、期中考试、期末考试乃至中考使用本题组进行训练、考试。

命制思路：三角形的周长就是三角形三边的长相加，即△PCD的周长=PC+CD+PD，由于C、D分别为OA、OB边上的一动点，所以三边长均处于变化之中，也就是该三角形三个顶点中有两个顶点在移动、三条边都在变化，考查学生如何发现在变化的过程中那些不变的关系，要想尽办法使动点处于两个定点之间的连线上，这就是考查学生空间想象能力。

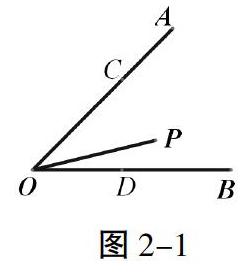
点P是定点，那就还要在两个动点所在的路线上做文章，把动点所在的直线作为对称轴，作定点P关于对称轴的对称点就可以实现上述两个目标。如图2-2，∠AOB=45°，作点P关于直线OA的对称点P′，连接P′C，则有P′C=PC，再作点P关于直线OB的对称点P′′，连接P′′D，则有P′′D=PD，这样可以把△PCD的周长转化即PC+CD+PD=P′C+CD+P′′D，这样三角形的周长就转化两个定点P′与P′′之间的连线长，根据“两点之间线段最短”，连接线段P′P′′，如图2-3，当点C移动到线段P′P′′与直线OA的交点C′处，点D移动到线段P′P′′与直线OB的交点B′处时，PCD的周长就是线段P′P′′的长，此时根据轴对称性∠P′′OD=∠POD，且∠P′OC=∠POC，继而∠P′OP′′=∠P′′OD+∠POD+∠POC+∠P′OC=2（∠POD+∠POC）=2∠AOB=2×45°=90°，另外，再根据轴对称的性质知道P′O=PO=P′′O，此时的△P′OP′′是等腰三角形，可以求出线段P′P′′的长。同样的思路适用于问题（2）。

实际上，本题可以推广到一般的情况，得到一个定理：△P′OP′′是等腰三角形，∠P′OP′′=2∠AOB，线段P′P′′的长是△PCD的周长最小值。可以命制∠AOB是直角或者钝角的题，这样使本题的数学价值发挥到极致，也有助于帮助学生在“做数学”的过程中领略数学之美之巧之妙，提升其数学素养。

学生在“做”中感悟轴对称图形的数学本质，然后再通过图形的运动确认或者用综合法论证探索得到结论。用图形运动的方式确认探索得到的结论，有利于不断发展学生对图形直观把握的能力，逐步形成一种审视、处理问题的方式。将探索和证明有机地结合在一起，可以引导学生不断地感受证明是探索活动的自然延续和必要发展，知晓合情推理和演绎推理都是人们正确认识事物的重要途径。