浅析优化初中数学二次函数教学的方法

李尔布

摘要：二次函数是初中教学中的一个难点，在初中数学的所有知识点中，它对学生的抽象思维和逻辑思维能力提出了更高的要求。新課改之后，二次函数的知识点有所改变。很多学生反映在学习二次函数的过程中感觉到比较困难。本文就优化初中数学二次函数的相关教学方法进行探讨。

关键词：初中数学；二次函数；教学方法

初中数学在整个数学教学中占据着非常重要的地位。二次函数又可以说是整个初中数学中非常重要的内容之一，同时二次函数的内容又比较抽象，所给老师的教学也造成了不小的难度。那么老师应该如何通过二次函数的教学来更好地让学生掌握关于函数的相关知识点呢？这篇文章让我们大家一起来分析一下。

一、对概念的理解

很多同学之所以对二次函数的学习感到困难，最重要的原因就是他们对二次函数的概念不是很理解。二次函数是由一次函数进化而来的，它指的是自变量的最高幂的次数为2。抛物线y=ax2+bx+c（a不等于零）[1]，a不等于零是这个算式得以成立的先决条件。很多同学不知道为什么a不能等于零（如果a等于零，代入计算的话，这个二次项就会变为一次函数）。例如：二次函数y=（m+2）xImI+3mx+1是关于x的二次函数，则m= ；若是关于x的一次函数，则m= .通过这样一个练习的训练学生就能够更好地理解二次函数和一次函数了。

二、二次函数的教学方法

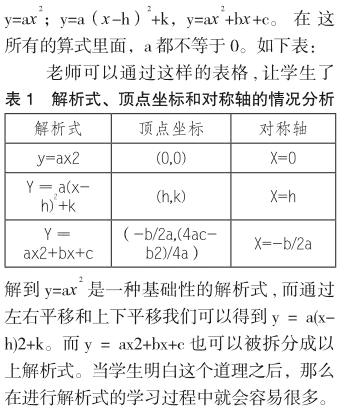
2、利用图像进行教学。二次函数虽然是比较抽象的数学知识，但是老师可以在教学的过程中通过图像让学生觉得不那么枯燥。

例如：如果将二次函数y=x2-2x-3这个解析式的图像向上平移两个单位，然后再向右平移一个单位，则可以得到新的解析式是什么？

可以将整个函数解析式化为顶点式y=（x-1）

2-4，则可以得到a的值为1，其顶点坐标为（1，-4）。如果能够将其图像向上平移2个单位，然后再向右平移一个单位，那么其顶点的坐标也会随之改变。而如果同学不能够很好地从算式中探究出其顶点的坐标的话，那么就可以通过画图的方式判断其顶点的坐标。通过画图可以看出其顶点的坐标为（2，-2），只要通过画图就可以知道平移并没有使得其开口的方向得以改变。则可以得出其平移后的解析式为y=（x-2）-2。

所以，通过上面这样一个例题，我们可以清楚地从图像中知道，二次函数的顶点在第几象限，抛物线的开口是朝上还是朝下的。抛物线的走向是如何的。因为有些同学的抽象思维毕竟有限，很难能够通过单纯的算式推断出一次函数和二次函数的相关情况。这就是图像在函数学习中的作用。

在数学二次函数的题目中经常有这样平移旋转变化的题目，很多同学不能够熟记平移或者旋转之后二次函数的变化，那么就可以通过作图的方式来顺利地写出解析式和做出题目。通过作图的方式，整体解析式也不会变得如此抽象。

3、让学生自己通过二次函数的算式进行推敲。很多学生之所以对二次函数在图像上的呈像不是很了解，最根本的原因就是不会对二次函数的算式进行更好地推敲。例如：已知抛物线经过两个点（0，3）和（4，6），对称轴为x=5，求这条抛物线的解析式[3]。那学生先可以用公式推算出相关的解析式，然后再通过画图来更好地验算一下自己所求的解析式是否正确。而学生在自己计算的过程中才能够更好地了解二次函数真正的意义。

三、结语

以上总结了二次函数的教学方法。重点是要通过图像把二次函数变得更加形象化，同时要抓住二次函数学习的三大关键：顶点、开口方向和对称轴。最终让学生通过多做题目的方式来更好地加深对二次函数的理解[4]。

参考文献

[1] 赵玲萍.初中数学二次函数的教学思路分析[J].中学时代，2012，（3）：126-129.

[2] 刘伟华.新课程下如何激发学生学习数学的兴趣[J].数学学习与研究，2013，（8）：132-135.

[3] 欧阳碧燕.浅谈初中二次函数的教学[J].师道教研，2012，（6）：135-138.

[4] 郭来恩.初中数学二次函数教学的探析[J].中国校外教育，2013，（8）：138-142.endprint