一类参数化PID观测器的分析与设计

尹晓丽

(山西大学商务学院 基础教学部，太原 030006)

0 引言

观测器是根据系统的输出估计系统状态的一类系统。上世纪60年代初期，为了对无法直接观测的控制系统实现状态反馈，文献[1-4]提出状态观测器的概念和构造方法，解决了状态不能直接量测的问题。观测器技术自提出以来，在控制工程的许多方面得到了实际应用，例如滤波[5]、扰动估计[6]、故障诊断[7]等。

为了降低观测器的超调，一些学者试图利用估计误差的积分和导数信息改善观测器性能：文献[8]在观测器设计中采用了误差的比例积分反馈，改善了观测器的性能；文献[9]针对系统存在干扰情况，利用线性矩阵不等式设计了比例积分观测器,在能量有界的外界干扰情况下,设计了具有干扰抑制的状态观测器,使得干扰对观测器性能的影响被限制在一定范围内。以上文献仅用到了误差的比例和积分信息，未用到误差的导数信息。文献[10-11]利用广义线性系统作为工具设计了一类PID观测器，同时用到了误差的比例，积分和微分信息，但设计过程较为复杂。针对观测器的设计始终缺少一种像控制中的PID算法那样能够充分利用误差的比例、积分和微分信息获得比较满意的性能和设计简单的算法，本文提出的算法试图弥补这一缺陷。

1 问题描述

本文考虑如下单输入单输出离散线性系统：

(1)

其中x∈Rn是系统状态，u∈R是系统控制输入，yx∈R是系统量测输出。

针对系统(1)，设计状态观测器如下：

(2)

其中，z∈Rn是观测器的状态向量，uo(k)是待设计的观测器调节项。yz∈R是观测器的输出。

令e=x-z，ye(k)=yx(k)-yz(k)，由(2)和(1)，得到状态估计误差系统如下：

(3)

仅仅利用估计误差设计uo(k)的观测器面临收敛快、超调严重的问题，必须在抑制超调和加快收敛速度之间寻求一个折中方案，这是该类观测器性能无法突破的瓶颈。为了提高收敛速度，同时避免超调，我们必须利用更多的量测误差信息。因此，利用量测估计误差及其时滞信息，设计观测器(2)的调节项为：

uo(k)=K1ye(k)+K2ye(k-1)+K3ye(k-2)

(4)

其中，Ki∈Rn×1(i=1,2,3)是待设计参数矩阵。(4)中ye(k)、ye(k-1)、ye(k-2)的不同线性组合可以近似反映累积误差、当前误差、误差变化率以及误差变化加速度，选取适当的参数矩阵K1、K2、K3便可以充分利用误差的比例、积分、微分信号，以达到在加快收敛速度的同时在一定程度上避免大的超调。

下面，对观测器参数设计进行理论分析。现将(4)带入(3)，得：

(5)

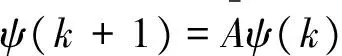
(6)

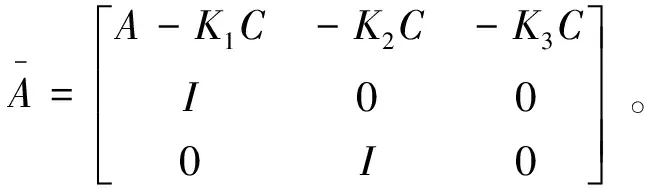
则

(7)

本文的目的是为系统(1)设计状态观测器(2)，使得误差系统(3) 渐近稳定。该问题等价于设计参数矩阵K使得系统(6)渐近稳定。

2 算法设计

本节将分析具有观测器反馈项(4)的系统(6)渐近稳定的条件，并给出(4)的一种简单参数设计方法。

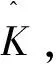
(8)

(9)

则系统(6)渐近稳定。

证明：构造一个Lyapunov函数：

V(k)=ψT(k)Pψ(k)

(10)

其中，P是待确定的正定矩阵。

(11)

则离散系统(6)渐近稳定的充要条件是：存在矩阵P>0，使得:

(12)

利用矩阵运算的性质可得：

⟺

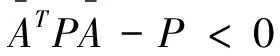
(13)

则

因此，若线性矩阵不等式组(8)-(9)成立，即(13)成立，则存在矩阵P>0，使得(12)成立，即离散线性系统(6)渐近稳定，证毕。

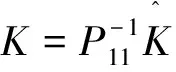
(14)

上述过程从理论上分析了观测器设计方法的可行性。下面，提出一类简单的参数设计方法，在实际使用中可以简化参数的设计过程，无需进行复杂的数学计算，直接根据经验选取参数并适当调整，便可获得满意的观测器估计效果。

(15)

其中α、β、γ都是标量，分别代表估计误差比例项、积分项、微分项的权重。

设计估计误差反馈增益

(16)

其中ki代表估计误差反馈在观测器不同通道上的增益，一般情况可以全部设置为1。将K的三个列向量作为Ki(i=1,2,3)带入(4)，即得到系统(1)的状态观测器(2)。

3 仿真实验

考虑以下线性系统：

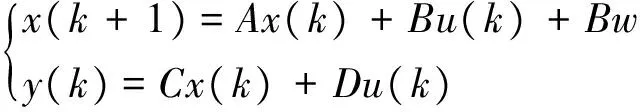
(17)

其中，x∈R3表示状态向量，u∈R表示控制信号，w表示扰动信号，y∈R为系统的输出信号，这里将量测输出信号设置为状态向量的第2个分量，下面将利用观测器对不能直接量测的第三个状态变量进行估计。

系统(17)的参数配置如表1所示。

表1 系统(17)的参数配置 (Matlab代码表示)

系统状态变量的初始状态全部设置为0，仿真运行时间区间为：k从0到300。控制器信号取为：

u=0

(18)

扰动信号取为：

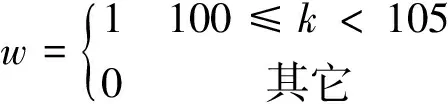
(19)

基于在算法设计部分所提方法，可以设计观测器(2)的待定参数矩阵，见表2，其中观测器状态变量的初始值均设置为0。我们将观察扰动发生后观测器对系统状态变量的估计是否快速准确且超调很小。

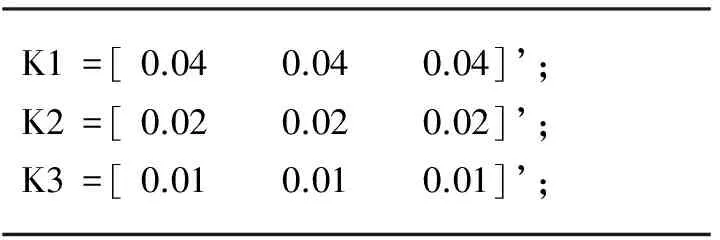
表2 观测器参数(Matlab代码表示)

设系统(17)的3个状态分量分别为x1、x2、x3，其中x2为系统量测输出，x1和x3为不可量测的待估计信号。对信号x3进行估计。当扰动导致系统状态发生变化时，观测器能对不可量测的状态分量x3进行估计，并很快收敛到x3的真实轨迹。估计误差过程中没有发生明显的超调。还可以根据(15)式所示的参数设计方法，适当调整参数α、β、γ的值以改变观测器的收敛速度。该实验充分说明了本文提出的参数设计方法是简单有效，且完全可行的。

4 结论

本文针对单输入单输出离散线性系统给出了一种新的系统状态观测器设计方法，并从理论上证明了该方法的可行性。同时介绍了一种简单实用的参数设计办法。仿真结果表明，该观测器对于系统任意设定的初始状态，能以微小的超调很快达到收敛。该观测器设计方法可用于改进基于观测器输出对被控对象进行控制的控制算法，将具有比较广阔的应用场景。

[1] MAJIME H, HINO H.Design of optimal observers for linear time-invariant systems[J]. International Journal of Control, 1974, 19(5): 993-1004.

[2] KIM C G, KUDVA P, GOURISHANKAR V.An optimal observer design for discrete linear systems[J]. International Journal of Control, 1978, 27(6): 879-884.

[3] WILLEMS J L.Design of state observers for linear discrete-time systems[J]. International Journal of Systems Science, 1980, 11(2):139-147.

[4] ASTROM K J.Theory and Application of Self-tuning Regulators[J]. Automatica, 1977, 13(5): 457-476.

[5] CACACE F, GERMANI A, PALUMBO P.A new approach to nonlinear filtering via a mixed state observer and polynomial scheme[J]. IFAC Proceedings Volumes, 2011, 44(1): 4477-4482.

[6] CHEN M, LIN S, TSENG Mi, et al.Robust State-and-Disturbance Observer Design for Linear Non-minimum-phase Systems[J]. Asian Journal of Control, 2016, 18(3): 1135-1141.

[7] WEI X, VERHAEGEN M.Robust fault detection observer design for linear uncertain systems[J]. International Journal of Control, 2011, 84(1): 197-215.

[8] SÖFFKER D, YU TIE-JUN, MÜLLER PETER-C.State estimation of dynamical systems with nonlinearities by using proportional-integral observer[J]. International Journal of Systems Science, 1995, 26(9): 1571-1582.

[9] 王占山,张化光. 具有干扰抑制的PI观测器的设计及其应用[J]. 吉林大学学报(工学版), 2004, 34(2): 277-281.

[10] WU A G, FENG G, DUAN G R. Proportional multiple-integral observer design for discrete-time descriptor linear systems[J]. International Journal of Systems Science, 2012, 43(8): 1492-1503.

[11] WU A G, DUAN G R, FU Y M. Generalized PID observer design for descriptor linear systems.[J]. IEEE transactions on systems Man & Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man & Cybernetics Society, 2007, 37(5): 1390-1395.