变换图的张量积图

金晶晶

(福建船政交通职业学院 公共教学部，福建 福州 350007)

20世纪50、60年代， Ryser H J和Fulkerson D R等数学家对(0，1)-矩阵类U(R,S)(具体定义见第1节的定义1)进行研究并得到许多重要结论[1,2].U(R,S)的相关性质已广泛地应用于组合图论和网络流理论等领域中[1]. 1980年，著名的图论专家Brualdi R A定义了U(R,S)上的变换图G(R,S)[2]，并且提出关于变换图的连通性、直径与哈密尔顿性等问题[2]，许多学者随之做了进一步研究[3-11]. 对变换图G(R,S)结构方面的问题，Jin J J 自2011年起陆续研究一类变换图G(R*,S*)的基本性质并刻画其结构特征[8-11].

本文所涉及的图为简单图，未定义的术语参见文献[12].

1 变换图的定义

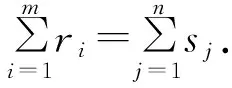
aij=0或1(i=1,…，m,j=1,…，n),

Brualdi R A定义的G(R,S)为无向简单图，其顶点集V(G(R,S))=U(R,S)，并且对任意A,B∈U(R,S),A，B在U(R,S)中相邻当且仅当A能经过一个变换得B.

2 变换图的张量积图

定义2 若A是一个m×n的矩阵，而B是一个p×q的矩阵，则矩阵的张量积(又称Kronecker-积)是一个mp×nq的矩阵[13]：

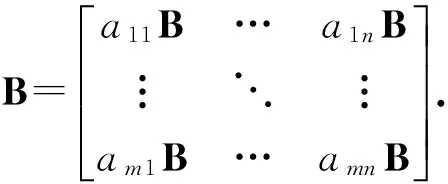
即，A⊗B是把A的每个元素代之以块aij⊗B而得. 矩阵的张量积是研究矩阵结构的重要工具. 近30年来，矩阵的张量积在结构矩阵方程理论和自动控制理论研究中得到重要应用.

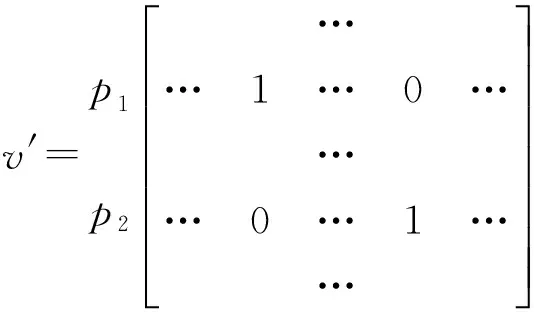
若G(R,S)是U(R,S)上的变换图，与v∈G(R,S)所对应的矩阵为A∈U(R,S).为方便表示，下面统一用v来表示其所对应的(0,1)-矩阵A.

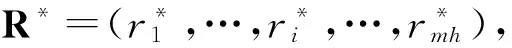
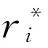
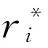
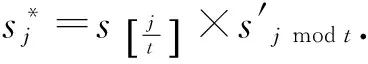
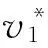
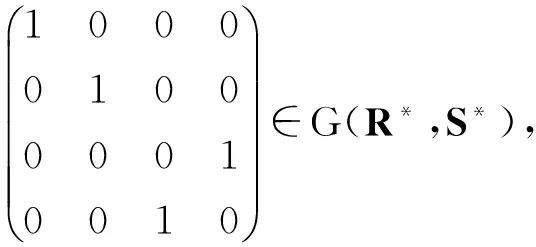
3 变换图的张量积图的若干性质

|V(G)|、|E(G)|和D(G)分别表示图G的顶点数、边数和直径. 由定义3和组合数学的乘法原理易得下面的定理.

定理2 |V(G1(R1,S1)⊗G2(R2,S2))|=|V(G1(R1,S1))|×|V(G2(R2,S2))|.

由定理2得，|V(G1(R1,S1)⊗G2(R2,S2))|≠0当且仅当|V(G1(R1,S1))|≠0且|V(G2(R2,S2))|≠0.

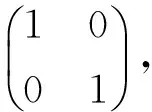
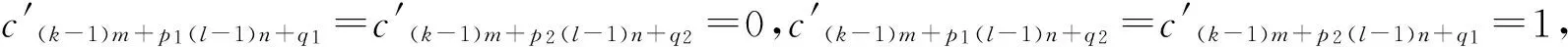
综上，|E(G1(R1,S1)⊗G2(R2,S2))|≠0.

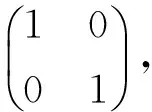
q1q2j1j2

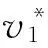
情形2 情形1证明了v*=v⊗v′时定理3的必要性成立，下面证明v*=v′⊗v时定理3的必要性亦成立.

j1j2q1q2

由定理3立即得：

定理4 |E(G1(R1,S1)⊗G2(R2,S2))|=max{|E(G1(R1,S1))|,|E(G2(R2,S2))|}.

定理5 |D(G1(R1,S1)⊗G2(R2,S2))|=max{|D(G1(R1,S1))|,|D(G2(R2,S2))|}.

[1] Brualdi R A. Matrices of zeros and ones with fixed row and column sum vectors[J].Linear Algebra and its Applications, 1980, 33：159-231.

[2] Ryser H J. Combinatorial properties of matrices of zeros and ones[J]. Canadian Journal of Mathematics, 1957,9：371-377.

[3] 陈荣斯, 郭晓峰, 张福基. 一类0.1 矩阵变换图的边连通性[J]. 新疆大学学报(自然科学版), 1988, 5(1): 17-25.

[4] Li X L, Zhang F J. Hamiltonicity of a type of interchange graphs[J]. Discrete Applied Mathematics, 1994, 51(1/2)：107-111.

[5] Brualdi R A，Shen J. Disjoint cycles in Eulerian digraphs and the diameter of interchange graphs[J]. Journal of Combinatorial Theory Series B, 2002, 85(2)：189-196.

[6] 钱建国. 变换图的直径及Brualdi 猜想[J]. 数学学报, 2002, 45(2)：411-416.

[7] Yuster R. Packing 4-cycles in Eulerian and bipartite Eulerian tournaments with an application to distances in interchange graphs[J]. Annals of Combinatorics. 2005, 9(1):117-124.

[8] Jin J J. Some properties for a class of interchange graphs[J]. Discrete Applied Mathematics,2011, 159(17)：2069-2077.

[9] 金晶晶. 一类变换图的距离性质[J]. 吉首大学学报(自然科学版), 2012, 33(4): 31-36.

[10] 金晶晶. 一类变换图的递归构造方法[J]. 湖南工程学院学报(自然科学版), 2013, 23(4): 45-48.

[11] 金晶晶.每行和为1 的(0,1)方阵变换图的若干性质[J]. 宁德师范学院学报(自然科学版), 2015,27(3): 237-240.

[12] Bondy J A, Murty U S R. Graph theory with its applications[M]. Wisconsin: The MacMillan Press Ltd, 1976.

[13] 柳柏濂. 组合矩阵论[M]. 北京：科学出版社, 2005.