高核过渡金属簇合物的电子计数规则的研究

金成树，马松艳，迟云超，王佩华，金凤友，李方泰

(绥化学院 食品与制药工程学院，黑龙江，绥化152061)

对于非稠合型过渡金属簇合物，闭式、巢式、网式、敞网式或这些结构类型的加帽结构多数符合Wade规则、稀有气体规则(包含八偶律和十八电子规则)的处理结果.如每个过渡金属原子参与成键的价轨道是9个，并且无单电子存在时，由Wade规则可知NVE = 2 (CVMO) = 2 (n + 6 M + N + 1)，SEP = NVE/2-n-6M = N + 1.其中，NVE表示簇合物的价电子总数，CVMO表示簇合物中被电子占据的成键和非键分子轨道数，n表示骨架表面上的主族原子数，M表示骨架表面上的过渡金属原子数.N表示闭式结构的顶点数，SEP表示簇成键价电子对数.

对于非稠合型过渡金属簇合物，Lauher用EHMO方法[1]计算了一些裸Rh簇骨架结构的CVMO值.当然，理论上Lauher的EHMO方法对任何骨架结构应该都适用.与Wade规则类似，Lauher的EHMO方法也存在很多例外情况.对于某些三帽和四帽八面体，Lauher的EHMO方法的计算结果与Wade规则的预期结果不符，误差较大.

对于稠合型过渡金属簇合物，分骨架间仅含共点而不含共边和共面情况时mno规则是适用的[2].分骨架间含共点、共边和共面的稠合型过渡金属簇合物，Mingos稠合规则是适用的[3].Teo的C2模型[4]能应用于共点、共边和共面的双八面体或双二十面体结构(即闭式-12顶点结构)等的稠合型过渡金属簇合物.对于稠合型过渡金属簇合物，唐氏拓扑结构规则能加以推广应用[5].对于大多数稠合型过渡金属簇合物，Teo的C2模型、Mingos稠合规则与本文作者提出的稠合规则等都是等效的[5]，但对高核过渡金属簇合物基本不适用.下面将介绍和讨论高核过渡金属簇合物中的各种电子计数规则.

1 没有考虑任何结构的高核过渡金属簇合物的电子计数规则

1980年Ciani和Sironi[6]用扩展的休克尔分子轨道理论(即EHMO方法)处理了大量的裸Rh的高核密堆积过渡金属簇合物，总结出了高核过渡金属簇合物遵守的公式为

NVE = 2 CVMO = 2 (6 M + X)

(1)

其中，M项表示所有的过渡金属原子数.X值的变化范围为6～11，一般情况下X=7.

1991年唐敖庆和李前树认为高核过渡金属簇合物应符合下列3个公式，即[7,8]

NVE = 2 (6M + 6)

(2)

NVE =2 (n + 6M + 9)

(3)

NVE = 2 (6M + 7) + m

(4)

其中，M项表示所有过渡金属原子数，n项表示填隙主族原子数，m项表示填隙主族原子中的价电子总数.(3,4)式适用于含填隙主族原子的高核过渡金属簇合物.(4)式也可应用于不含填隙主族原子的高核过渡金属簇合物中.

2 考虑部分结构的高核过渡金属簇合物的电子计数规则

1985年Mingos考虑了填隙过渡金属原子所组成的结构，认为高核过渡金属簇合物应符合下列3个公式，即

NVE = 12Ms+Δi

(5)

NVE = 12Ms+24

(6)

NVE = 12Ms+2Ms+2

(7)

其中，Ms表示骨架表面上的过渡金属原子数.Δi表示与填隙过渡金属原子(Mi)所组成的结构和填隙主族原子(ni)有关的特征数值.如Mi=1时，Δi=18；Mi=2(组成了线形结构)时，Δi=34.Mi=3(组成了线形结构)时，Δi=50.Mi=3(组成了三角形结构)时，Δi=48(或50).Mi=4(组成了四面体结构)时，Δi=60.Mi=4(组成了蝴蝶形结构)时，Δi=62.Mi=6(组成了八面体结构)时，Δi=86.含4个填隙过渡金属原子(组成了蝴蝶形结构)和4个填隙主族原子的簇合物，如[H6-nNi34(CO)38C4]n-(n=6,5)，Δi=62+4ni=78.(6,7)式仅适用于含1个填隙过渡金属原子的簇合物.1988年，Mingos把(7)式改写为NVE=12(Ms+Mc)+2Ms+2，Mc表示骨架表面上的加帽过渡金属原子数[9].

1983年Teo提出了扩展的Hume-Rothery规则[10]，把高核密堆积簇合物中的骨架表面上的过渡金属原子与填隙过渡金属原子分开处理，开拓了人们认知高核密堆积簇合物电子结构的视野.对于不含填隙过渡金属原子或含主族填隙原子的高核密堆积簇合物，该规则是不适用的.有许多簇合物的密堆积方式很难确定(选择时主观人为因素大)，这是该规则最大缺欠之处，故很少被应用.

1985年Teo等提出了高核过渡金属簇合物的壳规则[4]，考虑了填隙过渡金属原子所组成的结构，认为高核过渡金属簇合物符合的公式应为

NVE = 2 ( 6 Ms+ Bn) 或 CVMO = 6 Ms+ Bn

(8)

其中，Ms表示骨架表面上的过渡金属原子数，Bn表示壳电子对数.对于高核过渡金属簇合物，(8)式可改写为

NVE = 2 ( 6 M + K ) 或 CVMO = 6 M + K

(9)

这里，K值与高核过渡金属簇合物中心结构的B值有关，如果簇合物中心不含填隙过渡金属原子或由填隙过渡金属原子间组成了一定的中心结构时，K=B1.假如簇合物中心仅含有一个填隙过渡金属原子时，K值与中心的单核填隙过渡金属原子所处的外围骨架结构相关，K=B0.B0和B1的具体数值见文献[4].Teo的壳规则与Mingos的高核电子计数规则基本上是等效的.

3 考虑内部和表面结构的高核过渡金属簇合物的电子计数规则

各种稳定的高核过渡金属簇合物一般情况下应符合下列公式[5]

NVE = 2 (4 ns+ 9 Ms-Ls+ Li+ x Mi+ Z) + K

(10)

其中，ns和Ms分别表示整个骨架表面上所拥有的主族原子数和过渡金属原子数.Ms项包括骨架表面上加帽的过渡金属原子数.Ls表示骨架表面上的边数.Li表示由填隙原子间所形成的边数.(NVE)W表示用Wade规则计算的NVE值或用Lauher的EHMO方法计算的NVE值.(NVE)L表示用稀有气体规则计算的NVE值.(NVE)W与(NVE)L之间的差值为2Z，即Z = [(NVE)W- (NVE)L]/2.Mi0表示被埋藏在Z值大于零的分骨架内部的填隙过渡金属原子.Mi表示没有被埋藏在Z值大于零的分骨架内部的填隙过渡金属原子数(Mi项和Mi0项互不包含)，x是Mi项的系数.在(10)式中的K表示成单的价电子数，可由实验测定其数值.因此，被成对价电子占据的理论上的价分子轨道总数为4ns+ 9Ms-Ls+ Li+ xMi+ Z. [2(4ns+ 9Ms-Ls+ Li+ xMi+ Z) + K-NVE(obs.)]/2为正值时，表示过渡金属原子的空价轨道数或过渡金属原子参与形成的空成键分子轨道数，NVE(obs.)是价电子数的观察值即实际NVE值.[2(4ns+ 9Ms-Ls+ Li+ xMi+ Z) + K-NVE(obs.)]/2为负值时，表示超预期增多的过渡金属原子的价轨道数或过渡金属原子参与形成的成键分子轨道数.

应用(10)式时注意如下事项：

(1)某原子被假想是填隙原子时，如它与其他表面原子能构成五角锥、六角锥或更大的多角锥，则这个假想的填隙原子位于锥顶时应是表面原子而不能看作填隙原子.

(2)填隙过渡金属原子间形成化学键后，假设构成了簇合物中的内部骨架，每个填隙过渡金属原子都有一个价轨道中的电子将变为内部骨架的非骨架成键电子，但它们无法计入到表面骨架的非骨架成键电子中，故其系数为正值.一般情况下(即无空价轨道存在时)，填隙过渡金属原子间成键后，Mi项的系数x取值是1.不与其他填隙过渡金属原子成键的填隙过渡金属原子Mi项应看作配位原子，在不考虑空价轨道存在的情况下，它的系数x取值是零.

(3)Li项中的电子应看作是内部骨架的骨架成键电子，故该项系数值应为正.Mi0项应看作配体，但Mi0项与其他原子间可存在化学键.Mi0项不参与构成内部骨架，Mi0项也不参与构成Li项.埋藏在骨架结构内部的边称为隐藏边，Ls项不包括任何形式的隐藏边.

(4)Z值大于零的分骨架不要重复计算或考虑.由于Lauher的EHMO方法和Ciani-Sironi规则的计算结果对除Ni原子外的其他原子(特别是Au，Pt，Pd，Os等)构成的骨架是不可靠的，故一般情况下八面体的Z值取为1(除由Ni原子构成的Z值大于零的加帽八面体外).一般情况下，应用(10)式时Z值大于零的分骨架是指最简单的闭式结构、巢式结构、四方反棱柱(Z = 1)、单帽四方反棱柱(Z = 4)及双帽三棱柱(帽要加在四边形面上)(Z = 2)等笼状结构.四方反棱柱和双帽三棱柱的Z值是根据Lauher的计算结果确定的.

(5)在含过渡金属原子的主族原子簇合物中，被明显占多数的主族原子所包裹的Mi0项中的每个填隙过渡金属原子，对(10)式的影响结果是需要额外加10个价电子.除上述情况之外，在高核过渡金属簇合物中的所有主族原子包括骨架结构表面上的主族原子都应看作是配位原子.ns项中不包括加帽的和填隙的主族原子.

4 考虑内部和表面结构的高核过渡金属簇合物的电子计数规则公式的应用和讨论

在表1中对(10)式的计算值与(5,6)式的计算值进行了比较，没有考虑高核过渡金属簇合物中可能存在的空价轨道和成单电子的影响.对含填隙主族原子的高核过渡金属簇合物，(5,6)式的计算结果优于Teo等的壳规则.

表1 (10)式的计算值与(5,6)式的计算值的比较

注：表1中一般簇合物的Z值都是由八面体引起的.表1中第三列a是Lauher计算的价电子数，b是Ciani和Sironir计算的价电子数.表1中第四列c是根据(6)式计算的，其余是根据(5)式计算的.

[Rh15(C)2(CO)28]-中含2个八面体，不含填隙过渡金属原子，而两个碳原子间不存在化学键，故Z=2，见表1.根据(10)式可知该簇合物的NVE=200，根据(3,4)式可知该簇合物的NVE=202，而实际的观察值为200.对于该簇合物，Mingos的高核电子计数规则不适用.

[Ni16(CO)23C4]4-中4个填隙碳原子间形成了2个碳碳双键(平均键长为1.38Å)，不含填隙过渡金属原子，故Li=4，见表1.根据(10)式可知该簇合物的NVE=224，根据(4)式可知该簇合物的NVE=222，而实际的观察值为226.对于该簇合物，Mingos的高核电子计数规则不适用.

[Rh17(S)2(CO)32]3-中2个填隙硫原子与1个填隙Rh原子间形成了1个铑硫双键和1个铑硫单键(键长分别为2.17 Å和2.33 Å)，故Li=3，见表1.根据(10)式可知该簇合物的NVE=230，根据(4)式可知该簇合物的NVE=230，根据(5)式可知该簇合物的NVE=218(Δi=18Mi+4ni=18+8=26)，而实际观察值为232.

[Pt19(CO)22]4-中包含3个含隐藏边的五角双锥体(每个含隐藏边的五角双锥体的Z值为1)(见图1左)，2个填隙原子Mi项间存在化学键(化学键隐藏在五角双锥体内部)，故Mi=2，x=1，Li=0，Z=3.根据(10)式可知该簇合物的NVE=246，而实际观察值为238，可预测该簇合物中可能含有4个空价轨道未参与CVMO的形成或含4个空成键分子轨道，这与Lauher的计算结果完全一致.而(5)式的结果与实际一致，故(5)式没有(10)式所包含的预测能力.

(Me2PhP)10Au12Ag7(NO3)9中包含2个二十面体(每个二十面体的Z值为7)(见图1右)，2个填隙原子Mi0项间存在化学键(每个填隙原子都被包裹在二十面体内部)，该簇合物不存在Mi项，故Mi=0，Li=0，Z=14.根据(10)式可知该簇合物的NVE=244，根据(5)式可知该簇合物的NVE=238，实际的观察值为238.根据(10)式可预测该簇合物中可能含3个空价轨道未参与CVMO的形成或含3个空成键分子轨道.

图1 [Pt19(CO)22]4-和(Me2PhP)10Au12Ag7(NO3)9的结构

[(p-Tol3P)10Au13Ag12Cl7]2+、[(Ph3P)10Au12Ag12PtCl7]+和[(Ph3P)10Au13Ag12Cl8]+的结构中都包含2个二十面体[5](见图2左)，每个二十面体内都埋藏一个填隙原子，填隙原子间存在化学键(1个填隙原子属于Mi项，2个填隙原子属于Mi0项)，故Mi=1，x=0，Li=0，Z=14.根据(10)式可知该簇合物的NVE=314，而实际的观察值分别为310、310和314.根据Mingos的高核电子计数规则，该簇合物的NVE应为314.

[(p-Tol3P)10Au13Ag12Br8]+、(MePh2P)10Au12Ag13Br9和[(Ph3P)10Au13Ag12Br8]+的结构中都包含3个二十面体[5]，每个二十面体内都埋藏一个填隙原子(见图2右)，该簇合物中存在3个Mi0项，故Mi=0，Li=0，Z=21.根据(10)式可知该簇合物的NVE=318，与实际情况一致.根据Mingos的高核电子计数规则，该簇合物的NVE应为314.

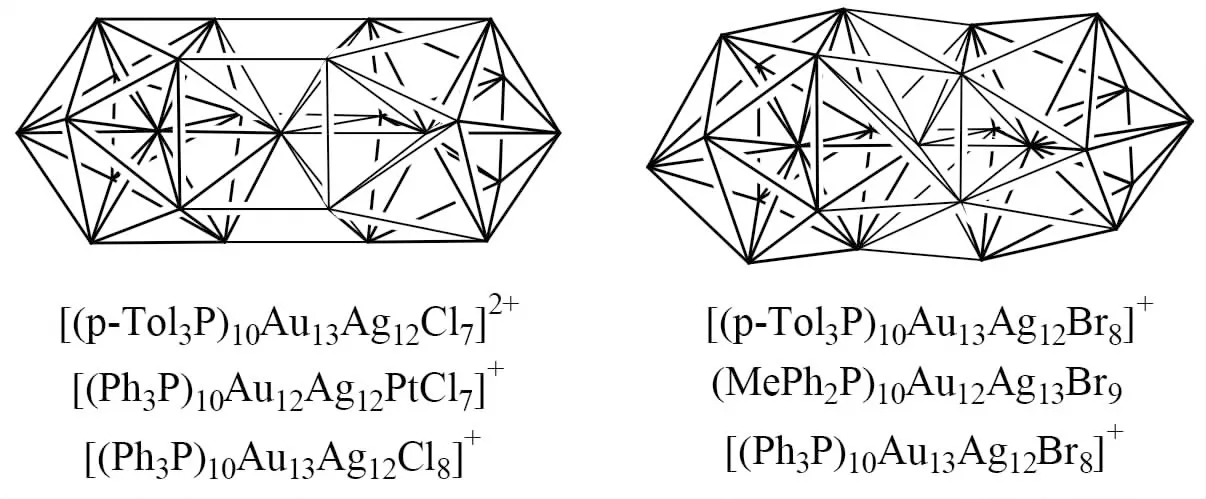
图2 (MePh2P)10Au12Ag13Br9和[(p-Tol3P)10Au13Ag12Cl7]2+等的结构

对于1个填隙过渡金属原子，如果有1、2或3个价轨道是不参与成键的空价轨道时，则与它相应的NVE值将比实际观察值多2、4或6个价电子.当高核过渡金属簇合物中表面过渡金属原子数超过50个时，(10)式计算值偏高趋势非常明显，说明过渡金属原子特别是填隙过渡金属原子中的空价轨道数目增加.对于骨架内部空间所包裹的Mi0项，如是金、银、钯、锇、铂原子等，常使NVE值减小.而铜、银、金、锌、镉、汞等原子参与形成簇合物的能力比较弱，存在形成金属键的惰性，它们形成的簇合物常偏离各种理论、规则或模型，计算值常偏大.

把簇合物中非稠合型结构看成稠合型结构，或把稠合型结构看成非稠合型结构都会出现错误.当然，这也是很难处理准确的问题，人为性很大.有些簇合物的结构中原子间是否成键判断起来很困难，出现取舍的问题.原子间的键长变化范围比较宽，但由经验可知在每个簇合物中所有的同一种单键的共价键长的变化范围应在最小单键长的基础上增加15%～25%之间为宜[5].

5 结论

高核密堆积的过渡金属簇合物中的成键情况和结构的联系非常复杂多变.对于高核过渡金属簇合物，(10)式与唐敖庆和李前树的电子计数规则及Mingos的电子计数规则的结果相比较不存在明显的优势.不难发现，唐敖庆和李前树的电子计数规则和Mingos的电子计数规则都必须考虑填隙主族原子中的价电子的影响，而与上述两个规则相似的Teo等的壳规则没有考虑填隙主族原子中的价电子的影响.因此对于含填隙主族原子的高核过渡金属簇合物，Teo等的壳规则的计算误差较大.(10)式没有考虑填隙主族原子中价电子的影响，但对含填隙主族原子的高核过渡金属簇合物是适用的.(10)式把Wade规则和稀有气体规则推广应用于高核过渡金属簇合物中，不但考虑了高核过渡金属簇合物的表面结构，也考虑了它们的内部结构，结果令人满意.由于(10)式适用面最广，人为因素小，故利用(10)式预测高核密堆积簇合物的实际成键情况比较合理.

[1] Lauher J W. The bonding capabilities of transition metal clusters Ⅳ. Three classes of carbonyl cluster compounds[J]. Journal of Organometallic Chemistry, 1981, 213: 25-34.

[2] Jemmis E D, Balakrishnarajan M M, Pancharatna P D. Electronic requirements for macropedral boranes[J]. Chemical Reviews, 2002,102:93-144.

[3] Mingos D M P. Polyhedral skeletal electron pair approach[J]. Accounts of Chemical Research, 1984,17:311-319.

[4] Teo B K, Zhang H. Counting electrons and rationalizing structures of clusters and clusters of clusters[J]. Polyhedron, 1990,9(15-16):1985-1999.

[5] 金成树. 簇合物的规则和热力学第二定律[M]. 哈尔滨:黑龙江科学技术出版社，2016.

[6] Ciani G, Sironi A. The stoichiometries of high-nuclearity transition metal carbonyl cluster compoundsⅠ.Compact close-packed clusters[J]. Journal of Organometallic Chemistry, 1980,197:233-248.

[7] 唐敖庆,李前树.过渡金属羰基化合物的结构规则[J]. 中国科学：B辑, 1988(1):1-7.

[8] 唐敖庆,李前树.原子簇化合物的结构规则与化学键性质[J]. 中国科学：B辑, 1991(7):673-679.

[9] Mingos D M P, Lin Z. A Theoretical analysis of high-nuclearity metal carbonyl clusters[J]. Dalton Transactions, 1988:1657-1664.

[10] Teo B K. A simple electron counting rule for close-packed high nuclearity metal clusters[J]. Chemical Communications, 1983:1362-1364.

[11] Chini P. Large metal carbonyl clusters (LMCC)[J]. Journal of Organometallic Chemistry, 1980,200:37-61.

[12] Ceriotti A, Longoni G, manassero M, et al. Synthesis and X-ray structure of [Ni16(CO)23C4]4-: a tetracarbide anionic cluster containing two interstitial C2fragments[J].Chemical Communications, 1985:1402-1403.

[13] Nunokawa K, Ito M, Sunahara T, et al. A new 19-metal-atom cluster [(Me2PhP)10Au12Ag7(NO3)9] with a nearly staggered staggered M5ring configuration [J]. Dalton Transactions, 2005:2726-2730.

[14] Tran N T, Kawano M, Powell D R, et al. Isostructural [Au6Pd6(Pd6-xNix)Ni20(CO)44]6-and [Au6Ni32(CO)44]6-clusters containing corresponding nonstoichiometric Au6Pd6(Pd6-xNix)Ni20and stoichiometric Au6Ni32nanosized cores: substitutional Pd/Ni crystal disorder (coloring problem) at only six specific nonadjacent pseudoequivalent metal sites in the 38-atom trimetallic close-packed framework[J]. Journal of the American Chemical Society, 1999,121(25):5945-5952.

[15] Femoni C, Iapalucci M C, Longoni G, et al. New high-Nuclearity Ni-Pt carbonyl clusters:synthesis and X-ray structure of the ordered [HNi24Pt17(CO)46]5-and the substitutionally Ni/Pt disordered [Ni32Pt24(CO)56]6-cluster anions [J]. Chemical Communications, 2004(20):2274-2275.

[16] Ceriotti A, Demartin F, Longoni G, et al.Synthesis and structure of the [Ni38Pt6(CO)48H6-n]n-(n=5, 4) ions: Ni-Pt clusters as models for “cherry” crystallites[J]. Angewandte Chemie International Edition in English, 1985,24(8): 697-698.

[17] Femoni C, Iapalucci M C, Longoni G, et al. Homoleptic carbonyl Ni-Pd clusters: synthesis of [Ni16Pd16(CO)40]4-and [Ni26Pd20(CO)54]6-and structural characterization of [NnBu4]4[Ni16Pd16(CO)40][J]. Angewandte Chemie International Edition, 2000,39(9):1635-1637.

[18] Mednikov E G, Ivanov S A, Dahl L F. [Pd30(CO)26(PEt3)10]and [Pd54(CO)40(PEt3)14]: generation of nanosized Pd30- and Pd54-core geometries containing interpenetrating cuboctahedral-based metal polyhedra[J]. Angewandte Chemie International Edition, 2003,42(3):323-327.