(α，α)-直觉模糊子群的构造

李华萍，李玉瑛

(太原理工大学 数学学院，山西 晋中 030600)

1965年，ZADEH[1]首先提出了模糊集的概念，自此模糊集作为普通集合概念的推广，逐渐被应用于数学各个分支。1971年，ROSENFELD[2]引入了模糊子群的概念，然后各种模糊代数的理论相继出现。其中，BHAKAT et al[3-4]利用模糊点与模糊集的邻属关系给出了(α,β)-模糊子群的定义。20世纪80年代，ATANASSOV[5]又提出了直觉模糊集的概念。2003年，HUR et al[6]提出了直觉模糊子群的概念。此后直觉模糊子群的理论研究进一步成熟。在2010年，YUAN et al[7]利用“点-集”邻属关系的方法，建立了模糊点与直觉模糊集的邻属关系，并利用这种邻属关系给出了(α，β)-直觉模糊子群的定义。2013—2016年，LI et al[8-10]使用截集的方法对(λ,μ)-模糊子群和子环进行了深入的研究。

本文基于(α,β)-直觉模糊子群及其各种截集的定义，首先，通过对其截集的研究，对(α,α)-直觉模糊子群作了进一步的研究。其次，给出了(α,α)-直觉模糊正规子群的定义，并讨论了它们的性质。

1 预备知识

在本文中，所有结论都是建立在模糊集理论的基础上。为了方便起见，记F(X)为集合X的所有模糊子集的集合，并假设G表示具有单位元e的乘法群。

定义1[1]设A∈F(X)，∀λ∈[0,1],称Aλ={x∈X|A(x)≥λ}为A的λ截集。而称A(λ)={x∈X|A(x)>λ}为A的λ强截集。

定义2[5]设X是一个非空集合，μA:X→[0,1],vA:X→[0,1]为两个映射，若μA(x)+vA(x)≤1,∀x∈X,则称A=(X,μA,vA)为X上的一个直觉模糊子集，简记为：

A=(μA,vA),A(x)=(μA(x),vA(x)) .

用IFS(X)表示X上所有直觉模糊集构成的集合。

定义3[5]设X是一个非空集合，A,B∈IFS(X)，且A=(μA,vA),B=(μB,vB).

1)A⊆B⟺μA(x)≤μB(x)且vA(x)≥vB(x);

2)A=B⟺μA(x)=μB(x)且vA(x)=vB(x);

3)Ac=(vA,μA);

4)A∩B=(μA∧μB,vA∨vB);

5)A∪B=(μA∨μB,vA∧vB);

6) ∩i∈IAi=(infi∈IμAi,supi∈IvAi);

7) ∪i∈IAi=(supi∈IμAi,infi∈IvAi)，其中Ai=(μAi,vAi)∈IFS(X),i∈I,I为指标集。

定义4[2]设A∈F(G),若对任意的x,y∈G,

1)A(xy)≥A(x)∧A(y);

2)A(x-1)≥A(x).

则称A为G的模糊子群。

定理1[3]设A∈F(G),则下列命题等价：

1)A为G的模糊子群；

2) ∀x,y∈G,A(x-1y)≥A(x)∧A(y);

3) ∀λ∈[0,1],Aλ非空时是G的子群；

4) ∀λ∈[0,1],A(λ)非空时是G的子群。

定义5[12]设A为G的模糊子群，若对任意的x,y∈G,A(xy)=A(yx)，则称A为G的模糊正规子群。

定理2[12]设A∈F(G)则下列命题等价：

1)A为G的模糊正规子群；

2) ∀x,y∈G,A(xy)=A(yx);

3) ∀λ∈[0,1],Aλ非空时是G的正规子群；

4) ∀λ∈[0,1],A(λ)非空时是G的正规子群。

定义6[2]设A:X→[0,1]是一个映射，若存在λ∈[0,1],x∈X,满足

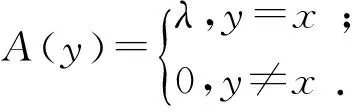
则称A为X的一个模糊点，并记为xλ.

定义7[2]设A是G的模糊子集，xλ是G中的一个模糊点，

1) 若A(x)≥λ,则称xλ属于A，记为xλ∈A;

2) 若A(x)+λ>1,则称xλ拟重于A，记为xλqA;

3) 若xλ∈A且xλqA，则记为xλ∈∧qA;

4) 若xλ∈A或xλqA，则记为xλ∈∨qA.

设A∈IFS(X)，在文献[7]中介绍了A的8个截集，本文仅用到了以下两个。

定义8[11]设A=(X,μA,vA)∈IFS(X),x∈X,且λ∈[0,1].

则称Aλ为A的λ-上截集。

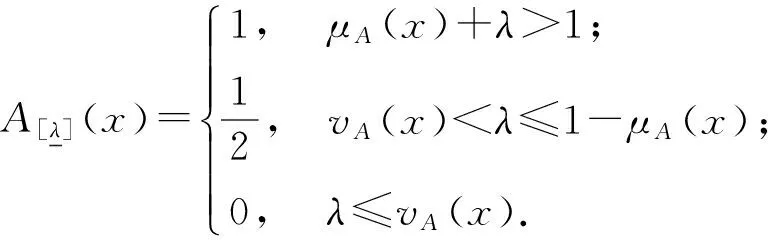
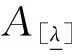
性质1[11]设A,B,At∈IFS(X),且λ∈[0,1]则下列结论成立：

2) (A∪B)λ=Aλ∪Bλ,(A∩B)λ=Aλ∩Bλ;

3) ∪t∈T(At)λ⊂(∪t∈TAt)λ,∩t∈T(At)λ=(∩t∈TAt)λ;

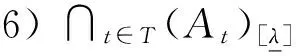
其中，T是指标集。

定义9[8]设xλ是X一个模糊点，A∈IFS(X)，令

它们分别表示xλ∈A和xλqA的隶属度。

性质2[8]设xλ是X一个模糊点，A∈IFS(X)，

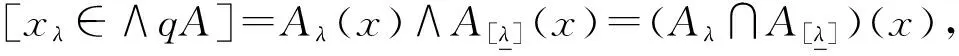
性质3[8]设xλ是X一个模糊点，Ai∈IFS(X),I是有限指标集，则有：

[xλ∈(∩i∈IAi)]=∧i∈I[xλ∈Ai] ,
[xλ∈(∪i∈IAi)]=∨i∈I[xλ∈Ai] ,
[xλq(∩i∈IAi)]=∧i∈I[xλqAi] ,
[xλq(∪i∈IAi)]=∨i∈I[xλqAi] .

20世纪80 年代，ATANASSOV[5]提出了直觉模糊集的概念；YUAN et al[8]在2010年时，给出了(α,β)-直觉模糊子群的定义，本文将采用定义10进行研究。

定义10[8]设A=(G,μA,vA)是群G的直觉模糊子集，α,β∈{∈,q,∈∧q,∈∨q}.若对任意的x,y∈G,s,t∈(0,1]，满足：

1) [xsytβA]≥[xsαA]∧[ytαA];

2 (α,α)-直觉模糊子群

本节将利用(α,α)-直觉模糊子群的概念，讨论(α,α)-直觉模糊子群的一些性质。为方便起见，在之后讨论中，我们假设λ∈[0,1],xλ是群G一个模糊点，α∈{∈,q,∈∧q,∈∨q}.

定义11 设A=(G,μA,vA)是群G的直觉模糊子集，若对任意的x,y∈G,s,t∈(0,1]，满足：

1) [xsytαA]≥[xsαA]∧[ytαA];

在定义11中，由于α可以选择4种关系，故可以得到4种(α,α)-直觉模糊子群。本节将研究这4种(α,α)-直觉模糊子群的性质。

定理3 设A为G的(α,α)-直觉模糊子群，则∀x∈G,s∈(0,1]，

1) [esαA]≥[xsαA];

证明:由定义11可得：

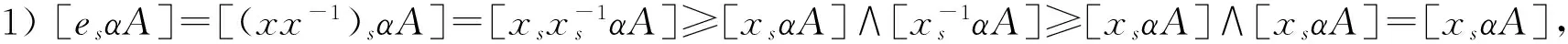
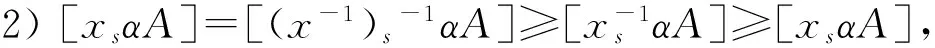
定理4 设A∈IFS(G)，则A为G的(α,α)-直觉模糊子群当且仅当

证明:若A为G的(α,α)-直觉模糊子群，则由定义11，对任意的x,y∈G：

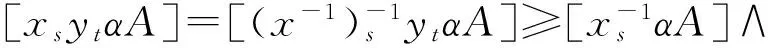
所以由定义11，A为G的(α,α)-直觉模糊子群。

定理5 设A为G的(α,α)-直觉模糊子群，x,y∈G,∀t∈(0,1].若

[xtαA]≠[ytαA]，则[xtytαA]=[xtαA]∧[ytαA].

证明：不妨设[xtαA]>[ytαA]，由定义11以及定理4可得：

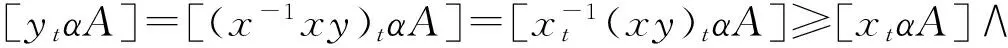
而[xtytαA]≥[xtαA]∧[ytαA]=[ytαA],

即[xtytαA]=[ytαA]=[xtαA]∧[ytαA].

定理6 设Ai为G的(α,α)-直觉模糊子群，其中α∈{∈,q,∈∧q},i∈I,I为有限指标集，则∩i∈IAi也是G的(α,α)-直觉模糊子群。

证明：对任意的x,y∈G,∀s,t∈(0,1],由性质3以及定理4得：

所以∩i∈IAi也是G的(α,α)-直觉模糊子群。

定理7A为G的(∈,∈)-直觉模糊子群的充分必要条件是∀s∈(0,1],As为G的模糊子群。

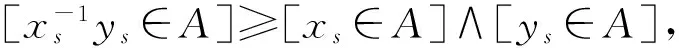
反之，若∀s,t∈(0,1],由题设可得，As∧t为G的模糊子群，由定理1得，As∧t(x-1y)≥As∧t(x)∧As∧t(y),即[(x-1y)s∧t∈A]≥[xs∧t∈A]∧[ys∧t∈A].

又由性质1中(1)得，

[xs∧t∈A]≥[xs∈A],[ys∧t∈A]≥[yt∈A],

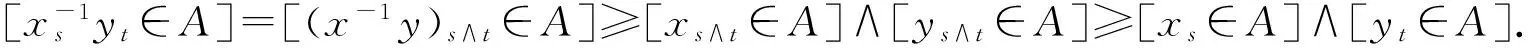
由定理7及定理1，易知定理8，定理9成立。

定理8 设A∈IFS(G),则A为G的(∈,∈)-直觉模糊子群的充分必要条件是∀λ∈[0,1],∀s∈(0,1],(As)λ非空时为G的子群。

定理9 设A∈IFS(G),则A为G的(∈,∈)-直觉模糊子群的充分必要条件是∀λ∈[0,1],∀s∈(0,1],(As)(λ)非空时为G的子群。

由定理10及定理1，易知定理11，定理12成立。

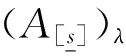
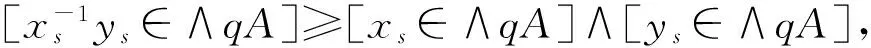
由定理13及定理1，易知定理14，定理15成立。

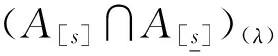
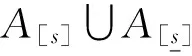
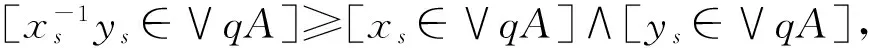
由定理16及定理1，易知定理17，定理18成立。

3 (α,α)-直觉模糊正规子群

本节给出(α,α)-直觉模糊正规子群的定义，在此基础上讨论其性质。

定义12 设A为G的(α,α)-直觉模糊子群，若∀x,y∈G,s∈(0,1],[(xy)sαA]=[(yx)sαA],

则称A为G的(α,α)-直觉模糊正规子群。

由定义12容易证明下面定理。

定理19 设A为G的(α,α)-直觉模糊子群，则A为G的(α,α)-直觉模糊正规子群的充分必要条件是[(xy)tαA]≥[(yx)tαA],∀x,y∈G.

定理20 设A为G的(∈,∈)-直觉模糊子群，∀s∈(0,1],则A为G的(∈,∈)-直觉模糊正规子群的充分必要条件是As是G的模糊正规子群。

证明：A为G的(∈,∈)-直觉模糊正规子群，从而A为G的(∈,∈)-直觉模糊子群，且∀x,y∈G,[(xy)s∈A]=[(yx)s∈A],由定理7，As是G的模糊子群，且As(xy)=As(yx).由定义5得，As是G的模糊正规子群。

反之，∀s∈(0,1],由已知As是G的模糊正规子群，从而As是G的模糊子群，且As(xy)=As(yx).由定理7，A是G的(∈,∈)-直壳模糊子群，且[(xy)s∈A]=[(yx)s∈A],由定义12可知，A为G的(∈,∈)-直觉模糊正规子群。

由定理20及定理2易知，定理21，定理22成立。

定理21 设A为G的(∈,∈)-直觉模糊子群，则A为G的(∈,∈)-直觉模糊正规子群的充分必要条件是∀s∈(0,1],∀λ∈[0,1],(As)λ是G的模糊正规子群。

定理22 设A为G的(∈,∈)-直觉模糊子群，则A为G的(∈,∈)-直觉模糊正规子群的充分必要条件是∀s∈(0,1],∀λ∈[0,1],(As)(λ)是G的模糊正规子群。

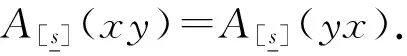
由定理23及定理2易知，定理24，定理25成立。

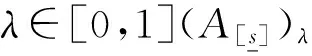
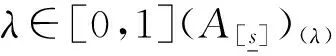
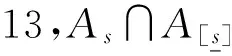
由定理26及定理2易知，定理27，定理28成立。

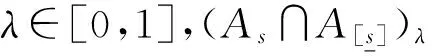
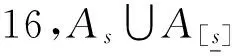
由定理29及定理2易知，定理30，定理31成立。

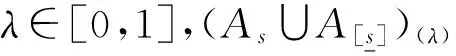
4 结束语

笔者在(α,β)-直觉模糊子群定义的基础上，对(α,α)-直觉模糊子群以及对(α,α)-直觉模糊正规子群进行了深入研究。关于(α,α)-直觉模糊正规子群还可以从另外角度加以研究，(α,α)-直觉模糊子群的运算等也是以后继续研究方向。

[1] ZADEH L A.Fuzzy sets[J].Information and Control,1965,8:338-353.

[2] ROSENFELD A.Fuzzy groups[J].Journal of Mathematical Analysis and Applications,1971, 35:512-517.

[3] BHAKAT S K,DAS P.On the definition of a fuzzy subgroup[J].Fuzzy Sets and Systems,1992,51:235-241.

[4] BHAKAT S K,DAS P.(ε,εvq)Fuzzy subgroup[J].Fuzzy Sets and Systems,1996,80:359-368.

[5] ATANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1):87-96.

[6] HUR K,KANG H W,SONG H K.Intuitionistic fuzzy subgroups and subrings[J].Honam Math J,2003,25:19-41.

[7] YUAN X H,LI H X,LEE E S.On the definition of the intuitionistic fuzzy subgroups[J].Computers and Mathematics with Applications,2010,59:3117-3129.

[8] LI Y Y,WANG X Z,YANG L Q.A study of (λ,μ)-fuzzy subgroups[J].Journal of Applied Mathematics.

[9] 李玉瑛，杨丽琼.(λ,μ)-模糊子群性质的研究[J].太原理工大学学报,2012,43(5):630-636.

LI Y Y,YANG L Q.A study on properties of (λ,μ)-fuzzy subgroups[J].Journal of Taiyuan University of Technology,2012,43(5):630-636.

[10] 李玉瑛，王绪柱，张贝贝.(λ,μ)-模糊子环和理想的进一步讨论[J].数学的实践与认识,2016,46(16):272-277.

LI Y Y,WANG X Z,ZHANG B B.A study on (λ,μ)-fuzzy subrings and ideals[J].Mathematics in Practice and Theory,2016,46(6):272-277.

[11] 袁学海，李洪兴，孙凯彪.直觉模糊集和区间值模糊集的截集、分解定理和表现定理[J].中国科学(F辑：信息科学),2009,39(9):933-945.

YUAN X H,LI H X,SUN K B.The decomposition theorem and represantation theorem of the fuzzy set of intuitionistic fuzzy sets and interval values[J].Science in China(Series F:Information Sciences),2009,39(9):933-945.

[12] 姚炳学.群与环上的模糊理论[M].北京:科学出版社,2008.