基于模糊聚类分析的风电功率预测研究

张传辉，田建艳,b，高 炜，王 芳,b

(太原理工大学 a.信息工程学院，b.电力系统运行与控制山西省重点实验室，c.机械工程学院，太原 030024)

风的间歇性和随机性导致了风电功率预测具有很大的不稳定性，特别是近年来风电场数量和装机容量不断增大，一旦将风电并入电网运行，这种功率波动将会给电网的运行造成不可估量的冲击[1]。因此，提高风电功率的预测精度，可以更好地保障电网的安全稳定运行、合理安排调度计划以及有效提高电网对风电的接纳能力等[2]。胡亚伟等[3]提出了基于横、纵向误差平移修正的风电功率预测精度改善方法，能有效提高预测精度。张露等[4]提出了基于不同优化准则的风电功率预测模型，与各单项预测模型及其他组合模型相比，优化模型的整体误差指标较小，有效地提高了预测精度。翟军昌等[5]针对传统的风电功率预测模型的不足，提出了一种参数自调整的风电功率预测方法，通过加权递推最小二乘方法建立预测模型，该方法具有较高的预测精度。ZHANG[6]在有限数据的情况下，采用一致预测方法，根据在不同高度上的风电数据对预测精度影响的不同，通过组合几种预测模型提高了预测精度。

人工神经网络具有并行处理、分布式存储以及容错性等特征，具有自学习、自组织和自适应能力[7]，被广泛应用于风电功率预测中，但是神经网络模型的建立对训练样本具有较高的依赖性，训练样本的选择既要包含足够广的选择范围，使得模型具有更强的泛化能力[8]，同时又要保证模型具有更快的预测速度和更高的预测精度。但是如果样本范围足够广，样本数量足够多，必然会影响模型预测的速度和精度。因此，保证范围足够广的样本数量的同时又能使得模型更具有针对性，将能在很大程度上提高模型的预测能力。为此，本文提出了基于模糊C均值聚类的神经网络建模方法。该方法首先对训练样本进行聚类，将相似的训练样本分为若干个聚类集，对每个聚类集分别建立相应的神经网络模型，计算预测样本与各聚类集的匹配度，将其划分到相似度最高的聚类集，采用相应的神经网络对风电功率进行预测，从而提高了神经网络模型的预测精度。

1 基于减法聚类优化的FCM聚类算法

1.1 FCM基本原理

聚类就是把事物间的相似性作为类属划分的准则，按照一定的要求和规律对事物进行区分并归类的过程[9]。在聚类算法中，模糊C均值(FCM)算法理论完善、应用广泛。FCM算法属于无监督学习方法，通过采用隶属度来表征每个样本点隶属于某个聚类的程度[10]。FCM算法原理如下：

将待聚类样本集X={x1,x2,…,xN}划分为c类，其中x1,x2,…,xN为聚类样本，N为样本数，2≤c≤N，且聚类中心矩阵为V=(v1,v2,…,vc)T，目标函数及其约束条件分别如式(1)和式(2)所示：

(1)

(2)

式中：uki为隶属度，表示第i(i=1,2,…,N)个样本属于第k(k=1,2,…,c)个类的程度；U为uki构成的隶属矩阵；vk为第k个聚类中心；dki为vk与xi之间的欧式距离，计算式为dki=‖vk-xi‖；m0为模糊参数，通常m0=2.

采用拉格朗日乘子求最优解，可以得到：

(3)

(4)

在聚类数(c)、模糊参数(m0)、最大迭代次数等聚类参数已知时，由式(3)，(4)反复迭代即可实现训练样本的聚类过程。

1.2 减法聚类优化FCM

FCM算法对初始聚类中心十分敏感，采用人为确定聚类数和随机初始化的方法对最终模型的预测精度产生影响，而减法聚类是一种快速近似聚类方法，它将所有的样本都作为聚类中心的可能解，然后根据样本本身的规律自动确定出较合理的聚类中心和聚类数[11-12]。本文引入减法聚类，将其与FCM相结合，以获取训练样本的最优聚类结果。

采用减法聚类获取聚类数c与初始聚类中心V*的具体方法为：

(5)

(6)

式中，rb为邻域半径，为了削弱各聚类中心之间的影响，通常取rb=1.5ra.

聚类有效性的评价标准公式如下：

(7)

式中：分子部分体现了各聚类内部的紧凑性，分子越小，说明各类内部越紧凑；分母部分体现了各聚类之间的独立性，当每个类之间的距离越大时，即分母越大，说明各类之间独立性越强。当Vxie(U,V,c)结果较小时，说明各聚类内部比较紧凑、各聚类之间比较独立，也就表明聚类分析结果较为合理[14]。

2 基于聚类分析的风电功率预测模型

2.1 模型评价指标的确定

为了能够全面对预测结果进行评价，本文选取可以体现预测值偏离实际值最大幅度的最大绝对误差(Emax)、可以体现预测模型对系统误差的宏观评价的平均绝对误差(EMA)、用来衡量误差的分散程度的均方根误差(ERMS)、可以体现预测模型总体性能的平均绝对百分比误差(EMAP)以及反映预测误差分布的误差标准差(ESD)作为评价指标，各指标的计算公式如下：

Emax=max(|et|) .

(8)

(9)

(10)

(11)

(12)

2.2 神经网络模型的选取

训练样本经过聚类之后会得到若干个聚类集，编号为D1,D2,…,Dc，c为聚类集的总个数。同时选取课题组建立小波神经网络模型M1、GABP神经网络模型M2、Elman神经网络模型M3、GRNN广义回归神经网络模型M4、T-S模糊神经网络模型M5作为预测模型。根据风电功率预测的时序性和对功率影响较大的因素的相关性分析，选取前一时刻风速X1、当前时刻风速X2、风向的正弦值X3、风向的余弦值X4以及温度X5共5个因素作为模型的输入，风电功率作为模型的输出Y.

采用D1,D2,…,Dn分别训练上述5种神经网络模型，得到模型M1,M2,…,M5.比较每一个聚类集对应的5种神经网络的误差指标Emax、EMA、ERMS、EMAP、ESD，合理选取模型作为该聚类集的解。具体的选取原则分以下两种情况。

2.2.1 单模型预测

综合考虑5种模型的预测误差评价指标，若第i个神经网络模型Mi的各项指标均最佳，即将Mi模型作为聚类集Di上对应的预测模型。

2.2.2 多指标融合评价

模型Mi和模型Mj的预测效果指标各有优劣，直接观察并不能分出哪个模型的预测效果最好。当单指标评价结果不一致时，采用多指标融合评价方法对模型进行融合评价[15]，该方法中将离差最大化与主观修正系数相结合，确定各模型的综合权重，计算综合评价值，得到模型的排序。将5种模型的融合评价值的平均值作为阈值，选取融合评价值大于阈值的模型作为该聚类集对应的预测模型。

当数据集对应一个模型时，则直接用该模型进行预测。当数据集对应多个模型时，采用融合预测方法，融合权重采用诱导有序加权平均(induced ordered weighted average,IOWA)算子[16]确定。与传统的方法不同，它考虑到单模型在不同时刻点的预测精度可能不同，因此把单模型各个时刻点上的预测精度值作为诱导值，并以最小误差平方和为准则建立目标函数来求解权重系数，进行融合预测。具体步骤如下：

设经过模型融合评价后共有m种单一模型，t时刻的实际风电功率序列为{yt}(t=1,2,…,n)，用m种单一模型对风电功率进行预测，第i种预测模型在第t时刻的风电功率预测值为yit，(i=1,2,…,m).设m种单一模型在融合模型中的权重为ω=(ω1,ω2,…,ωm)，且满足：

(13)

令第i种模型在第t时刻的预测精度为ait，其表达式为：

(14)

显然，ait∈[0,1].

若将预测精度ait作为预测值yit的诱导值，则m种单模型在第t时刻的预测精度和预测值构成了m个二维数组：

(〈a1t,y1t〉,〈a2t,y2t〉,…,〈ait,yit〉,…,〈amt,ymt〉)，

其中，ait为预测值yit排序的诱导值。将m种单一模型在第t时刻的预测精度a1t,a2t,…,ait,…,amt,按照从大到小的顺序排列，由预测精度序列产生的基于IOWA算子融合预测值为：

(15)

式中，a-index(it)表示第t时刻第i种模型的预测精度下标。

令ea-index(it)=yt-ya-index(it)，则n个时刻总的融合预测误差平方和为：

(16)

则以预测误差平方和为准则的基于IOWA算子的融合预测模型可以表示成如下最优化模型：

(17)

其约束条件为：

(18)

通过求取式(17)的值就可以得到ωi的值。

2.3 预测样本归类

本文首先根据预测样本到聚类中心的距离来判断该样本点属于哪个数据集，然后采用该数据集对应的预测模型对风电功率进行预测。由于高斯指标法[17]易于处理非线性数据，本文采用此方法对预测样本进行归类，步骤如下：

假设样本第s个风电功率影响因素的权重ωs∈[0,1]，且∑ωs=1.预测样本和数据集第s个因素的欧氏距离为：

(19)

式中：Xas为预测样本第s个因素；Xbs为数据集聚类中心第s个因素，则其第s个值的高斯指标为：

(20)

σs=σ×(smax-smin) .

(21)

式中：a为预测样本；b为数据集对应的聚类中心；σs为挠曲点；smax为第s个因素的最大值；smin为第s个因素的最小值；σ为常数，取值范围为[0,1].

计算出高斯指标后，利用式(22)即可求出预测样本和样本集的相似度：

(22)

式中：SIM(a,b)为相似度；ωs是权重值，通过计算相关性系数确定。SIM(a,b)越大，表明预测样本与该样本集越相似，则把该预测样本归为该数据集中。

3 仿真分析

笔者采用山西某风电场的实际数据进行了大量的仿真实验。由于篇幅所限，仅给出以下数据进行说明：以2015年一整年的数据作为训练样本进行聚类，采用2016年1月1日—1月4日的数据作为预测样本。

3.1 初始聚类中心及聚类数的确定

1) 本文取δ=0.5，采用减法聚类得到聚类数cmax=11和初始聚类中心V*：

2) 由上一步得到的聚类数和聚类中心对模糊聚类算法进行初始化。然后根据式(3)和式(4)可得到最终的隶属矩阵U和聚类中心V，然后计算聚类有效性函数值Vxie(U,V,c)，公式如下：

(12)

根据上面得到的聚类数和聚类中心对模糊聚类算法进行初始化。然后通过计算聚类有效性函数值Vxie(U,V,c)得出最合适的聚类数和聚类中心，求得不同的类对应的Vxie如表1所示。

表1 聚类数和对应的有效性函数值Table 1 The number of cluster and the values of validity function

由表1可知，当聚类数为8时，所得Vxie的值最小，因此将聚类数定为8个。

对预测样本进行聚类，得到的数据集为8个，数据集编号分别为D1，D2，D3，D4，D5，D6，D7，D8.

3.2 神经网络模型的选取

采用D1—D8分别对5种神经网络模型进行训练。比较每一个数据集对应的5种模型的误差，根据2.2节的原则，合理选取模型作为该聚类集的解，得到每种数据集对应的预测模型如表2所示。

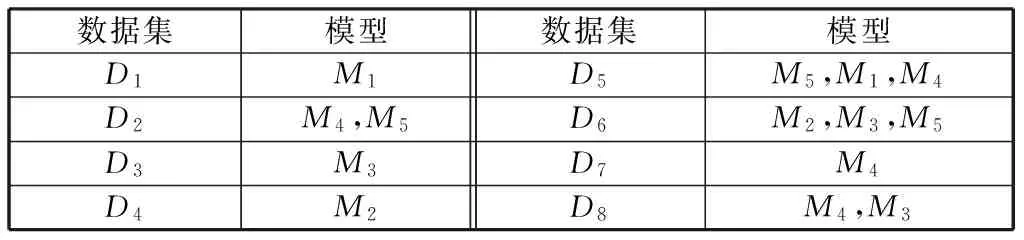
表2 每种数据集对应的预测模型Table 2 Each data set corresponding to the forecasting model

3.3 聚类建模结果

由表2可知，当聚类集对应唯一的预测模型时，就采用该模型进行预测；当聚类集对应多个模型时，则采用2.2节给出的融合方法求取融合模型的权重，最终的结果如表3所示。

表3 聚类建模结果Table 3 Results of clustering modeling

由表3可知，不同聚类集对应不同的模型进行风电功率的预测。将基于模糊聚类的神经网络建模用M6表示。

3.4 预测数据归类结果

预测模型库建立好以后，采用2.3节所述的方法对96组预测样本进行归类，归类结果如表4所示。

表4 每种聚类集对应的预测样本个数Table 4 Each data set corresponding to the number of samples

3.5 仿真分析

根据表4的聚类结果，归于不同聚类集的预测样本需要采用不同的神经网络模型进行预测。而传统的神经网络风电功率预测方法没有对预测样本进行聚类，所有预测样本都采用同一种神经网络模型进行预测。下面对两类方法的预测结果进行对比分析。

3.5.1 单模型预测效果分析

采用未经聚类的训练样本分别训练5种神经网络模型，利用每个模型分别对预测样本进行预测，以M1和M3模型为例说明单一模型的预测效果，其风电功率预测结果分别如图1和图2所示。

图1 M1模型的风电功率预测结果Fig.1 Wind power forecasting results of model M1

图2 M3模型的风电功率预测结果Fig.2 Wind power forecasting results of model M3

以预测误差绝对值为例，将预测误差超过42 kW(平均绝对误差值的120%)的时刻作为大误差点时刻，由图1和图2可知，神经网络模型单独预测时，在某些点的预测误差较大，比较明显的是M1模型中的第9点、12点、32点、75点等共25个大误差点数；M3模型中的26点、44点、53点、69点等共28个大误差点数。

3.5.2 基于聚类的神经网络模型预测效果分析

由表4可知，预测样本中有9组数据归为D1，再由表3可知这9组数据应该采用M1模型进行预测；有15组数据归为D2，应采用M4和M5模型进行融合预测；有7组数据归为D3，应采用M3模型进行预测，其他的预测样本也是根据其归属的聚类集不同，而选择不同的模型进行预测。所有样本最终的预测结果如图3所示。

图3 基于聚类的神经网络模型预测结果Fig.3 Wind power forecasting results of neural network model based on Clustering

由图3可知，基于聚类的神经网络模型的预测效果相对较好，如单一神经网络模型中出现误差较大的9点、26点、32点、44点、69点、75点等，在本方法中得到了较大的改善，大误差点数只有12个，整体预测精度明显提高。

3.5.3 各模型预测误差对比分析

为进一步说明不同方法的预测效果，将不同神经网络模型的各个预测误差指标列表如表5所示。

由表可知，5种单一神经网络模型中M4预测效果最好，EMA为21.07，EMAP为8.98%，而基于聚类的神经网络模型M6中EMA为16.74，EMAP为7.35%，相比较于M4，EMA减小18.1%，EMAP减小21%，其他指标均有不同幅度的减小。

表5 各个模型预测误差指标Table 5 Forecasting error of each model

为了进一步验证M6的预测效果，在2015年11月数据的基础上，同时增加2015年3月、6月和9月的各100组数据作为检验数据，每种模型的大误差点个数统计如表6所示。

表6 各个预测模型大误差点统计Table 6 The number of large error of each model

由表6可知，M6的风电功率预测误差在大的预测误差点上有了很大的改善，进而提高了模型的整体预测精度和稳定性。

4 结语

风的间歇性和随机性给风电功率预测带来了很大困难，针对神经网络模型的预测精度对训练样本依赖性较强的问题，本文提出采用基于聚类算法的神经网络对风电功率进行预测，研究结果表明：

1) 通过减法聚类来确定FCM的聚类中心，解决了FCM人为确定聚类数和初始聚类中心的问题，提高了FCM的聚类有效性。

2) 采用基于FCM的方法对数据进行聚类分析，然后进行神经网络模型的训练，既充分考虑了样本空间的特征，又使得模型具有针对性。采用山西某风电场的实际数据进行仿真研究，结果表明本文方法减少了预测模型的大误差点数，提高了模型的整体预测精度。该方法原理简单、步骤清晰、易操作，为提高风电功率的预测精度提供了一种可行的方法。

[1] 韩肖清,张健,张友民,等.风电场谐波分析与计算[J].太原理工大学学报,2009,40(5):540-544.

HAN X Q,ZHANG J,ZHANG Y M,et al.Analysis of harmonics in pinglu wind power plants in Shanxi province[J].Journal of Taiyuan University of Technology,2009,40(5):540-544.

[2] JUNG J,BROADWATER R P.Current status and uture advances for wind speed and power forecasting[J].Renewable and Sustainable Energy Reviews,2014,31(2):762-777.

[3] 胡亚伟,王筱,晁勤,等.采用横纵向误差平移插值修正的风电预测精度改善方法[J].电网技术,2015,39(10):2758-2765.

HU Y W,WANG Y,CAO Q,et al.Improvement of wind power forecasting accuracy using transverse error interpolation interpolation method[J].Power System Technology,2015,39(10):2758-2765.

[4] 张露,卢继平,梅亦蕾,等.基于不同优化准则的风电功率预测[J].电力自动化设备,2015,35(5):139-145.

ZHANG L,LU J P,MEI Y L,et al.Wind power prediction based on different optimization criteria[J].Electric Power Automation Equipment,2015,39(10):2758-2765.

[5] 翟军昌,葛延峰,梁鹏,等.一种参数自调整风电功率预测模型[J].东北大学学报,2016,37(2):153-156.

ZHAI J C,GE Y F,LIANG P,et al.A parameter self-adjusting wind power forecasting model[J].Journal of Northeastern University,2016,37(2):153-156.

[6] ZHANG F.Effect analysis of NWP wind speed at different height on the improvement of wind power forecast accuracy[C]∥4th International Conference on Energy and Environmental Protection (ICEEP).2015:3383-3387.

[7] 何东,刘瑞叶.基于主成分分析的神经网络动态集成风功率超短期预测[J].电力系统保护与控制,2013,41(4):50-54.

HE D,LIU R Y.Ultra-short-term wind power prediction using ANN ensemble based on the principal components analysis[J].Power System Protection and Control,2013,41(4):50-54.

[8] 武妍,张立明.神经网络的泛化能力与结构优化算法研究[J].计算机应用研究,2002,19(6):21-25.

WU Y,ZHANG L M.Research on generalization ability and structure optimization algorithm of neural networks[J].Computer Application Research,2002,19(6):21-25.

[9] 纪浩林,彭亮.基于聚类的超闭球算法短期风速预测研究[J].测控技术,2016,35(8):138-141.

JI H L,PENG L.Research on short-term wind speed prediction based on clustering algorithm[J].Journal of Measurement & Control Technology,2016,35(8):138-141.

[10] DUNN J C.A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J].Journal of Cybernetics,1974,3(3):32-57.

[11] GABRIELLA C,NICOLETTA D,CORRADO M.Subtractive clustering for seeding non-negative matrix factorizations[J].Information Sciences,2014,257(2):369-387.

[12] 董瑞,黄民翔.基于减法聚类的FCM算法在电力负荷分类中的应用[J].华东电力,2014,42(5):917-921.

DONG R,HUANG M X.Application of FCM algorithm based on subtractive clustering in power load classification[J].East China Electric Power,2014,42(5):917-921.

[13] NIKHIL R P,CHAKRABORTY D.Mountain and subtractive clustering method:improvements and generalizations[J].International Journal of Intelligent Systems,2000,15(4):329-341.

[14] WANG W N,ZHANG Y J.On fuzzy cluster validity indices[J].Fuzzy Sets and Systems,2007,158(19):2095-2117.

[15] TIAN J,LIU T,AMIT B,et al.Wind power forecasting model fusion evaluation based on comprehensive weights[C]∥Proceedings of ASME's International Mechanical Engineering Congress and Exposition.2016:1-9.

[16] YAGER R R.Induced aggregation operators[J].Fuzzy Sets and Systems,2003,137(1):59-69.

[17] 郑康宁,李向阳,杨凯.高斯-案例推理方法的预测模型及应用[J].运筹与管理,2011,20(6):99-105.

ZHENG K N,LI X Y,YANG K.Gaussian method in case-based reasoning and appIications[J].Operations Research and Management Science,2011,20(6):99-105.