基于高斯模型的工业过程数据的故障预测

杨为惠，陈彦萍，温福喜，高 聪

(西安邮电大学 a.计算机学院，b.大数据处理研究中心，西安 710121)

随着信息技术和自动化技术的快速发展，现代工业系统的集成度和复杂度越来越高。各部分之间的相互影响也越来越复杂，导致系统发生故障和功能失效的概率逐渐加大，且故障一旦发生，危害影响极大，严重的会导致系统整个失效和瘫痪。故障诊断就是在这种背景下，在故障已经发生后，确定故障的性质及其对未发生故障部分的影响，给出补救策略。

但如果在故障发生的早期，即在其还未对系统造成任何损害的情况下及时地检测出故障的发生，就可以提前实施可靠的维修策略排除故障，从而避免产品损坏、系统瘫痪以及灾难性事故的发生。基于这一背景，故障预测与健康管理(prognosis and health management，PHM)技术应运而生。

现代工业系统已经可以采集并且积累了海量的过程运行数据，基于数据驱动(data-driven)的故障预测方法[2]逐渐获得重视并取得快速发展。如何有效利用这些数据，依据一些智能算法来建立系统的故障预测模型，是保障复杂工程系统安全高效运行亟待解决的问题。而工业过程数据的非线性、小样本及自回归特性，以及故障预测中的不确定性问题等，为预测建模提升了难度[3]。

高斯过程[4]回归是近年发展起来的一种机器学习回归方法,它有着严格的统计学习理论基础, 对处理高维数、小样本、非线性等复杂的问题具有很好的适应性, 且泛化能力强。与神经网络、支持向量机相比, 具有容易实现、超参数自适应获取、非参数推断灵活以及输出具有概率意义等优点。

1 相关工作与背景知识

在故障预测中，预测方法是最基础，也是最核心的部分。

数据驱动故障预测方法主要集中在机器学习、计算智能或其他统计模型[6-7]。应用较为广泛和相对成熟的方法有自回归(AR)模型[8]，支持向量机(SVM)[9-10]，相关向量机(RVM)和神经网络(NN,neural network)[12-13]以及随机过程模型如马尔可夫模型、高斯过程回归模型等。

以上方法中，AR是线性模型，只适用于线性时间序列建模；其余方法为非线性模型，适用于工业过程中的非线性数据建模。文献[14]对NN建模技术进行了多步预测的预测性能研究，文献[15]提出先对时间序列进行EMD分解得到若干个分量，然后用神经网络模型分别对时间序列的EMD 分量进行多步预测，最后将该若干个分量作为输入，用神经网络模型进行时间序列的多步预测。文献[16]基于改进的小波神经网络算法对机床轴承故障进行预测。然而，神经网络的结构设计尚没有统一的理论依据，比如网络的层数、神经元的个数、传递函数的选择等，因此网络构建上有一定困难。神经网络的训练需要大量的数据，而在工业过程中往往只有少量的故障数据样本，样本缺乏致使网络性能下降。人工神经网络收敛速度慢，训练过程中存在过度拟合或拟合不足等问题，并且输出无概率意义，无法确定预测结果的置信度。

相关向量机、高斯过程回归模型这两种方法具备不确定性的管理能力[17]。较之NN模型，高斯过程具有完备的贝叶斯理论基础，在给出预测结果的同时还会给出一个置信区间，用作故障预测不确定性的度量。

文献[18]基于高斯过程建立TE仿真数据的单步预测模型，并将之运用于在线的故障检测，但是忽略了过程数据的时间序列特性。文献[19]提出用高斯过程模型对混沌时间序列进行单步与多步预测，并提出用混合的高斯过程核函数进行建模。尽管如此，以上文献提出的方法(包括基于NN模型的方法)，都是根据数据的统计特征建立模型，没有将数据具有的物理意义作为先验信息加入到模型中，而不同的工业过程、同一工业过程不同的模态下产生的数据都具有不同的物理特性。文献[20]提出了一种根据EMD分解环境监测数据,根据数据的物理特性构建核函数的方法。本文基于高斯过程回归(GPR,gaussian process regression)建立工业过程中时间序列数据的模型。通过针对特定数据构建高斯过程核函数来更好的描述数据特性，从而提升模型性能；并且在基于单步预测基础上，实现了不同种方法的多步预测。实验数据为在TE平台[5]上采集到复杂工业过程的模拟数据，通过大量的预测精度性能对比实验表明，构建的高斯过程预测方法较之对比的预测方法具有较高的平均预测精度。

2 基于高斯过程回归的故障预测

2.1 单步预测模型

2.1.1 高斯过程回归模型

假设观测目标值yi由一个未知函数f决定，并且被一个独立同分布的高斯噪声ωi腐蚀，即

yi=f(xi)+ωi.

(1)

式中：ωi为独立的随机变量，符合高斯分布，均值为0，方差为σ2(假设训练和测试数据的噪声具有相同的分布，即ωi∶N(0,K).

在高斯过程回归方法中，通常赋予f一个均值为0的高斯过程先验概率分布:

f|x,θ∶N|(0,K) .

(2)

式中：K是一个N×N维的对称正定的协方差矩阵，Ki,j=k(xi,yj),k(·,·)是协方差函数，也称核函数。它是一个以超参数θ为自变量的正定函数，因此，训练输出y的概率分布为：

y|x,θ∶N(0,K+σ2I) .

(3)

给定一个测试输入数据x*和对应的测试输出数据y*以及相应的先验概率分布抽样得到f(x*)，f(x)与f(x*)的联合概率分布也是一个均值为0的多维高斯过程：

(4)

其中，K*=[k(x*,x1),…,k(x*,xN)]T,K**=k(x*,x*).

基于式(1)中的高斯噪声假设，训练输出y和测试输出y*的联合概率分布为：

(5)

根据条件高斯法则，可以推导出

y*|y,x,θ,σ2∶N(m(x*),v(x*)) .

(6)

其中，预测值y*的均值m(x*)和标准差v(x*)为：

(7)

(8)

由此可以看出，已知协方差函数和它的超参数，就可以对未来时刻的数据做出预测。

2.1.2 模型训练

模型的训练就是获取协方差函数的参数最优值。目前GPR模型大多采用极大似然估计(maximum likelihood estimation,MLE)获得超参数的最优取值,即通过建立训练样本条件概率的对数似然函数，并对超参数求偏导，再采用共轭梯度优化方法搜索出超参数的最优解，具体求解过程可见参考文献[4].

其中对数似然函数的形式为：

(9)

对上式求偏导的结果为：

(10)

2.1.3 基于EMD的核函数构建方法

高斯过程的协方差函数为模型的训练增加了很大灵活性，但是怎样构建协方差函数就变成了一个难点。运用不同的核函数训练的模型性能会有较大的差距。以下为平方指数核函数(squared exponential，SE)，周期核函数(periodic，Per),线性核函数(linear，Lin)和二次有理数核函数(rational quadratic，RQ) 的表达式：

(11)

(12)

(13)

(14)

Merce原理指出，一个矩阵只要满足半正定就可以是一个协方差矩阵。通过将两个核函数相加和相乘的操作组合依然是一个有效的核函数。DAVID[21]在研究中总结了基本核函数所表述的数据特性和在组合后他们的特性变化规律。

在以上的核函数中，SE描述数据局部变化的特征，Per描述数据周期性变化的特征，并且是一个全局性的周期核函数，Lin描述数据的长期变化趋势，RQ描述数据的不规则变动；核函数的相加与相乘都会有相应的特性变化，例如，Lin核加Per核具有趋势周期特性，SE乘Per核函数具有局部周期的特性。

HUANG et al提出的经验模态分解(empirical mode decomposition,EMD)是一种基于信号局部特征的自适应分解方法[22]，可以有效地将原始时域信号分解为具有多尺度时频特性的本征模态函数(intrinsic mode functions,IMFs).该方法在旋转机械故障诊断领域、高层建筑和桥梁健康状态监测得到了广泛应用。工业过程中传感器监测到的过程数据分解得到的不同IMFs往往具有不同的物理含义[23]。

根据以上的规律，就可以依据特定数据的物理特性，构建具有针对性的高斯过程核函数，使模型具有更加好的预测性能。

2.2 基于时间序列的多步预测

2.2.1 预测策略

为了掌握更多的未来信息，需要对高斯过程模型进行多步预测[19]。多步预测是建立在上文单步的模型基础上的。预测策略是多步预测的重要研究内容。

在预测策略方面，现阶段应用的预测策略主要有迭代策略和直接策略。多步预测策略在TAIEB的文献[24]中有比较全面的阐述和研究。

2.2.1.1迭代策略

迭代预测策略中，首先需要建立单步预测模型，

yt=f(xt)+ω.

(15)

式中，xt={(xt,…,xt-d+1)}，yt，d为输入维数，即时延步数，ω是高斯噪声。

在接下来的迭代过程中，将yt当做其中一个输入变量，同时剔除时延最久的输入变量，从而在输入变量个数不变和模型不变的情况下实现下一时刻的yt+1预测，以此类推，直到预测得到yt+H-1.

2.2.1.2直接策略

直接多步预测策略，即在相同的输入数据的基础上对每一步预测建立相应的预测模型。每一步的预测输出值如下式：

[yt+h-1,yt+h-2,…,yt]=fh(xt,…,xt-d+1)+ω.

(16)

其中，yt，d为输入维数，ω是高斯噪声。

式中没有任何的预测输出作为下一时刻的输入，因此，多步预测误差并不会受到前面预测值的影响而不断的放大。然而，因为直接的多步预测之间关联性较弱，可能导致预测输出值偏差较大。

2.2.2 预测原理

高斯过程回归模型的预测方差不仅能够解释模型参数不确定性的影响，还可以描述过程的不确定性[17]。通过预测值和方差，可确定实际值可能的范围，以2倍方差来设置预测值的置信区间[yt+h-1-2σ,yt+h-1+σ]，其中，yt+h-1表示提前h步的预测值。从而确定可能出现故障的最早或者最迟时间。

3 实验验证

3.1 TE模拟平台

由于在实际情况中，对于任何大型工业过程而言，数据是无法公开得到的。为了验证本文提出的算法在时序数据异常检测中的有效性，选用了TE(Tennessee Eastman)仿真平台对本文算法进行验证。

TE化工过程是Eastman一个实际工艺流程的原型。整个过程包括5个主要操作单元，即反应器、冷凝器、循环压缩机、气液分离器和产品解吸塔。TE过程共有41个测量变量和12个操控变量，并设定21种故障类型。由于搅拌速度XMV(12)在反应过程中保持恒定不变，其对系统的建模没有任何影响，因而选择前52个变量[XMEAS(1),…,XMEAS(41),XMV(1),…,XMV(11)]T作为某一特定时刻的原始观测信号向量。

图1 TE工业过程原理图Fig.1 A process ftowsheet of the TE

在仿真实验中，设定TE过程总反应时间为48 h，采样间隔为3 min.所有的异常都是在仿真开始8 h后引进。因此此类故障的仿真可采集到48×20=960个数据样本，每个样本数据包含52维特征，每一类异常数据样本是一个960×52的样本矩阵。

接下来就以异常一为例进行实验。异常一的定义是A/C进料比发生了变化，主要影响的特征变量为XMSE(1)和XMSE(4).

异常一的XMSE(1)特征变量作为数据集a1，XMSE(4)特征变量作为数据集a2.每个数据集均包含了480个训练样本和960个测试样本。

3.2 对比实验

本节将提出的高斯过程模型与BP神经网络和应用最广泛的RBF核函数高斯过程模型进行对比，并与两种预测策略相结合，共形成6种多步预测方法：高斯过程迭代策略模型(GPI)、高斯过程直接策略模型(GPD)、神经网络迭代策略模型(NNI)、神经网络直接策略模型(NND)、高斯过程RBF迭代策略模型(GPrI)和高斯过程RBF直接策略模型(GPrD).

高斯过程模型的先验分布为自由度为4的Student's T分布。

在应用BP神经网络模型时，根据输入要求，设置输入节点个数为4，设置隐藏层的神经元个数为10.BP网络的训练函数为trainlm函数。

3.3 评价指标

本节采用均方根误差(RMSE)评价多步预测方法的性能。方根误差ERMS计算表达式为：

(17)

3.4 实验核函数构建

图2为原始数据通过经验模态分解得到的4个IMF分量。IMF1表达了数据有不规则变化与局部变化的物理特性，IMF2，IMF3与IMF4表示了数据有局部周期特性与周期特性。所以在核函数的构建中通过加入SE核与RQ核描述数据的局部变化与不规则变化，通过加入Per核函与SE核相乘来描述局部周期变化。

图2 原始数据与其IMF分量Fig.2 Raw data and its IMF component

最终构建的核函数为：

K=SE×Per+SE+RQ .

(18)

3.5 实验结果分析

首先，基于a1和a2数据集，比较GPI，GPD，GPrI，GPrD，NNI，NND 6种方法的五步预测结果。图3—图7为6种方法在a1数据集上五步预测的预测值与真实值的对比。可以明显看出，对神经网络而言，基于高斯过程模型的预测方法得到的预测值曲线与真实值曲线拟合得更好。

图3 a1数据集上GPD与GPI的五步预测结果与真实值对比Fig.3 Five-step ahead prediction results of GPD and GPI on a1 data set compare with the real value

6种预测方法对2种数据集的5步预测性能(通过RMSE计算得到)的统计结果如表1和表2所示，由于神经网络的方法需要交叉验证，故神经网络的RMSE是5次实验求平均值得到。

由表1和表2可以看出，本文提出的预测方法在两个数据集上的5步预测都有最小的RMSE.这说明提出的基于高斯过程的预测方法得到的预测值与其他方法相比更接近于真实的传感器测量值。而基于高斯过程的方法相较于神经网络都有较小的RMSE，表明高斯过程回归方法处理具有小样本特性的工业过程故障数据时更有优势，而神经网络模型的性能可能会因为训练样本不够充分而受限。

固定回归阶数P=4，预测步长依次为[1,5,10,20,50]，相应的预测结果的RMSE的变化情况如表3，表4所示。可以看出，随着预测步长的增大，各种方法的预测结果的RMSE呈逐渐增大的趋势。当步长低于20步时，一般迭代预测方法的RMSE低于直接预测方法，而当步长大于20时，往往直接预测取得更低的RMSE，这是因为迭代的过程中会累积误差，步长越大，迭代次数越多，误差就越大。特别地，GPD预测方法的RMSE绝大多数低于其他方法，表明在各种预测步长之下，提出的基于高斯过程的预测方法能够对工业过程数据进行更准确的多步预测。

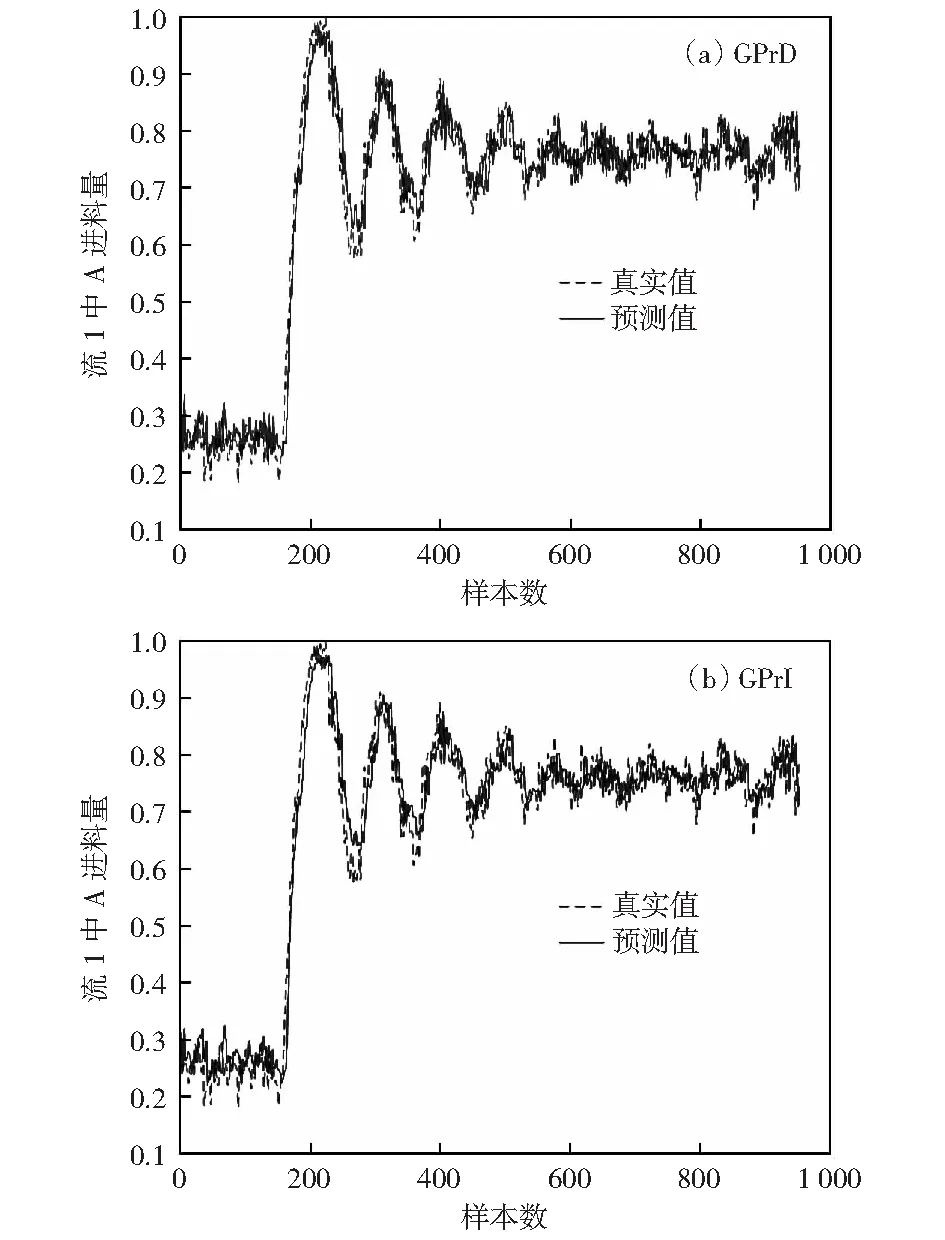
图4 a1数据集上GPrD与GPrI的五步预测结果与真实值对比Fig.4 Five-step ahead prediction results of GPrD and GPrI on a1 data set compare with the real value

图5 a1数据集上NND与NNI的5步预测结果与真实值对比Fig.5 Five-step ahead prediction results of NND and NNI on a1 data set compare with the real value

RMSEGPGPrNNI0.04100.04180.0578D0.04010.04130.0514

表2 a2数据集上5步预测的性能统计结果Table 2 The performance of 5-step ahead prediction on a2 data set

图6 a1数据集上GPI与GPrI的10步预测结果与真实值对比Fig.6 Ten-step ahead prediction results of GPI and GPrI on a1 data set compare with the real value

4 结束语

本文基于高斯过程模型对工业过程中的历史数据建立预测模型，通过对过程中监测变量的多步预测，实现了故障的提前预知。针对不同的工业过程，不同的工况，数据会呈现出不同的物理特性。通过分析特定数据的物理特性，构建出可以描述该特性的核函数；同时结合多种多步预测策略和建模方法，在TE模拟数据集上进行了一系列对比实验。实验结果表明，本文提出的方法有更好的预测精度。下一步将TE模型的更多种类故障数据上、在多模态情况下验证该方法的性能。

图7 a1数据集上GPD与NND的20步预测结果与真实值对比Fig.7 Twenty-step ahead prediction results of GPD and NND on a1 data set compare with the real value

表3 a1数据集上不同步长预测性能比较Table 3 The performance of multi-step ahead prediction based on different method on a1 data set

表4 a2数据集上不同步长预测性能比较Table 4 The performance of multi-step ahead prediction based on different method on a2 data set

[1] 曾声奎，MICHAEL G PECHT,吴际.故障预测与健康管理(PHM)技术的现状与发展[J].航空学报,2005,26(5):627-632.

ZENG S K,MIEHAEL G PECHT,WU J.Status and perspectives of prognostics and health management technologies[J].Acta Aeronautica et Astronautica Sinica,2005,26(5):627-632.

[2] 彭宇,刘大同.数据驱动故障预测和健康管理综述[J].仪器仪表学报,2014,35(3):481-495.

PENG Y,LIU D T.Data-driven prognostics and health management:a review of recent advances[J].Chinese Journal of Scientific Instrument,2014,35(3):481-495.

[3] 刘强,秦泗钊.过程工业大数据建模研究展望[J].自动化学报,2016,42(2):161-171.

LIU Q,QIN S Joe.Perspectives on big data modeling of process industries[J].Acta Automatica Sinica,2016,42(2):161-171.

[4] RASMUSSEN C E,WILLIAMS C K I.Gaussian processes for machine learning[M].London:The MIT Press,2006.

[5] ANDREAS BATHELT,LAWRENCE RICKER N,MOHIEDDINE JELALI.Revision of the tennessee eastman process model[J].International Symposium on Advanced Control of Chemical Processes,2014(9):

[6] HENG A,ZHANG S,TAN ACC,et al.Rotating machineryprognostics:State of the art，challenges and opportunities[J].Mechanical Systems and Signal Processing，2009，23(3):724-739.

[7] PENG Y,DONG M,ZUO M J.Current status of machine prognostics in condition-based maintenance:a review[J].The International Journal of Advanced Manufacturing Technology,2010,50(1/4):297-313.

[8] LIU D,LUO Y,PENG Y,et al.Lithium-ion battery remaining useful life estimation based on nonlinear AR model combined with degradation feature[C]∥Annual Conference of the Prognostics and Health Management Society 2012，Minneapolis，Minnesota，USA.2012:1-7.

[9] QU J,ZUO M J.An LSSVR-based algorithm for online system condition prognostics[J].Expert Systems with Applications，2012，39(5):6089-6102.

[10] WIDODO A,SHIM M C,CAESARENDRA W,et al.Intelligent prognostics for battery health monitoring based on sample entropy[J].Expert Systems with Applications,2011,38(9):11763-11769.

[11] 朱永利,尹金良.组合核相关向量机在电力变压器故障诊断中的应用研究[J].中国电机工程学报,2013,33(22):68-74.

ZHU Y L,YIN J L.Study on application of multi-kernel learning relevance vector machines in fault diagnosis of power transformers[J].Proceedings of the CSEE,2013,33(22):68-74.

[12] LIU J,SAXENA A,GOEBEL K,et al.An adaptive recurrent neural network for remaining useful life prediction of lthium-ion batteries[C]∥Annual Conference of thePrognostics and Health Management Society 2010.2010.

[13] PEEL L,GOLD I.Data driven prognostics using a Kalman filter ensemble of neural network models[C]∥International Conference on Prognostics and Health Management 2008.2008:1-6.

[14] GUO Z H,ZHAO H Y,LU H Y,et al.Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model[J].Renew Energy,2012,37(1):241-249.

[15] 谢景新,程春田,周桂红.基于经验模式分解与混沌分析的直接多步预测模型[J].自动化学报,2008,34(6):684-689.

XIE J X,CHENG C T,ZHOU G H.A new nulti-step ahead prediction model on EMD and chaos analysis[J].Acta Automatica Sinica,2008,34(6):684-689.

[16] LIU Q,LIU M,ZHANG F,et al.A fault prediction method based on modified genetic algorithm using BP neural network algorithm[C]∥2016 IEEE International Conference on Systems,Man,and Cybernetics.2016.

[17] 孙强,岳继光.基于不确定性的故障预测方法综述[J].控制与决策,2015,29(5):769-778.

SUN Q,YUE J G.Review on fault prognostic methods based on uncertainty[J].Control and Decision,2015,29(5):769-778.

[18] 于冰洁，夏战国，王久龙.基于高斯过程模型的异常检测算法[J].计算机工程与设计,2016,37(4):914-920.

YU B J,XIA Z G,WANG J L.Anomaly detection algorithm based on Gaussian process model[J].Computer Engineering and Design,2016,37(4):914-920.

[19] 李军,张友鹏.基于高斯过程的混沌时间序列单步与多步预测[J].物理学报,2011,60(7):143-152.

LI J,ZHANG Y P.Single-step and multiple-step prediction of chaotic time series using Gaussian process model[J].Acta Phys Sin,2011,60(7):143-152.

[20] 陈艳,王子健,赵泽,等.传感器网络环境监测时间序列数据的高斯过程建模与多步预测[J].通信学报,2015,36(10):252-262.

CHEN Y,WANG Z J,ZHAO Z,et al.Gaussian process modeling and multi-step prediction for time series data in wireless sensor network environmental monitoring[J].Journal on Communications,2015,36(10):252-262.

[21] DUVENAUD D,LLOYD J R,GROSSE R,et al.Structure discovery in nonparametric regression through compositional kernel search[C]∥Proc of the 30th International Conference on Machine Learning,Atlanta GA,USA.2013.1166-1174.

[22] HUANG N E,LONG S R,SHEN Z.The mechanism for frequency downshift in nonlinear wave evolution[J].Advances in Applied Mechanics,1996,32:59.

[23] CHEN J.Application of empirical mode decomposition in structural health monitoring:some experience[J].Advances in Adaptive Data Analysis,2009,1(4):601:621.

[24] TAIEB SB,SORJAMAA A,BONTEMPI G.Multiple-output modeling for multi-step-ahead time series forecasting[J].Neurocomputing,2010,73(10/12):1950-1957.