时间序列数据趋势转折点提取算法
2018-01-19,,,
,,,
(北京联合大学 a.信息学院;b.自动化学院,北京 100101)
0 概述
时间序列数据正在以一种难以想象的规模和速度快速增长,已经在商业、医药和科学研究等领域占据了大量的存储空间。对原始数据直接进行数据挖掘,不仅要花费大量时间,而且由于噪声点的存在还会导致算法准确度下降。在通常情况下,需要对原始序列数据进行数据的高级表示[1],常用方法有奇异值分解[2-3]、离散傅里叶变换[4-5]、离散小波变换[6-7]、主成分分析[8]和分段线性表示[9-10]等。
其中分段线性表示(PLR)方法是使用直线段近似表示时间序列,具有时间多解析性、支持快速相似性搜索和数据压缩度灵活等优点。而在分段线性表示方法中,分段点的选择显得极为重要。使用提取的分段点可以近似拟合原始数据和相似性度量等运算,大大减少运算成本。有许多学者已经在分段点提取方面做出贡献,如文献[11]提出用等宽度窗口中数据的平均值表示时间序列(PAA),文献[12]提出基于重要点的分段线性方法(PCA)。在国内,文献[13]提出根据相邻两点间斜率的变化提取时间序列上的分段点(SEEP),文献[14]提出基于一阶滤波的时间序列分段线性表示方法(SFWF),文献[15]提出基于序列重要点概念达到时间序列分割算法(SIP),文献[16]提出根据偏离度提取变化点的时间序列分段线性表示(CPA)。
本文给出一种提取时间序列数据趋势转折点算法(FTTO)。首先定义时间序列数据4个相邻数据点的运算,随后讨论运算结果P并且对P值小于零和等于零2种出现趋势转折点的情况分别进行讨论,然后提取原始数据中上升、下降和平缓3种基本趋势转折点。最后将相邻2个基本趋势转折点中间的数据做坐标旋转变换,对旋转变换得到的新的时间序列数据使用FTTO算法,得到缓慢上升、快速上升、缓慢下降、快速下降4种拐点。
1 基本定义
定义1(时间序列) 时间序列是有序的信息集合。每一个元素包括记录信息和时间。长度为n时间序列X记为:
X={
(1)
其中,
xi={a1,a2,…,am},m≥1
(2)
在一般情况下,时间序列的采样间隔Δt(Δt=ti+1-ti)相等且大于零,也可以将时间序列X简记为{x1,x2,…,xn}。
定义2(分段线性表示) 时间序列数据X记为{x1,x2,…,xn},趋势转折点集合为{xt1,xt2,…,xti,…,xtn},其中,xt1和xtn分别为时间序列的起始点和终点。其分段线性表示为:
XPLR= {
(3)
其中,
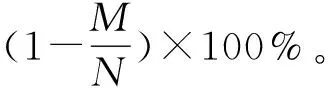
定义4在时间序列X中,如果xi是趋势转折点,那么xi必是局部极值点[15],即xi满足:
{(xi≥xi+1)∪(xi>xi+1)}∩
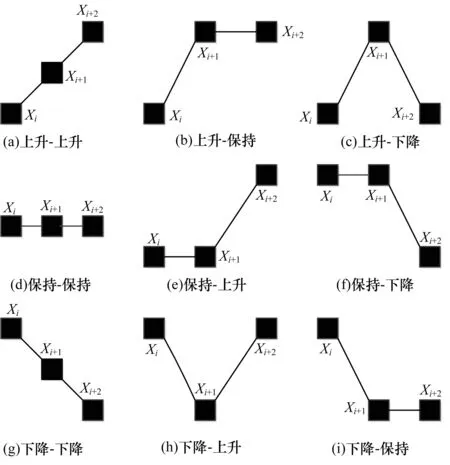
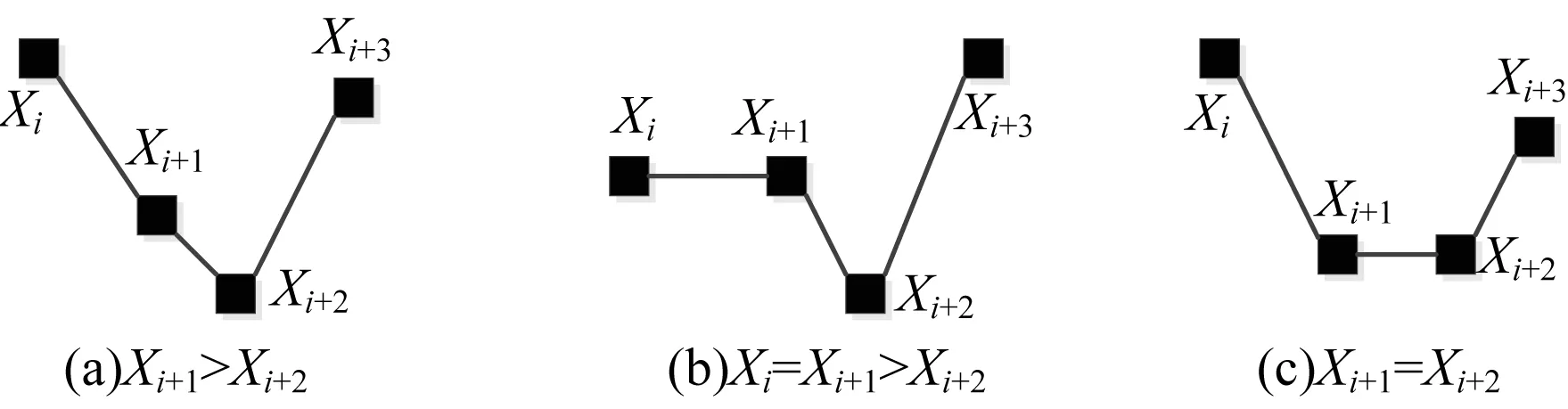
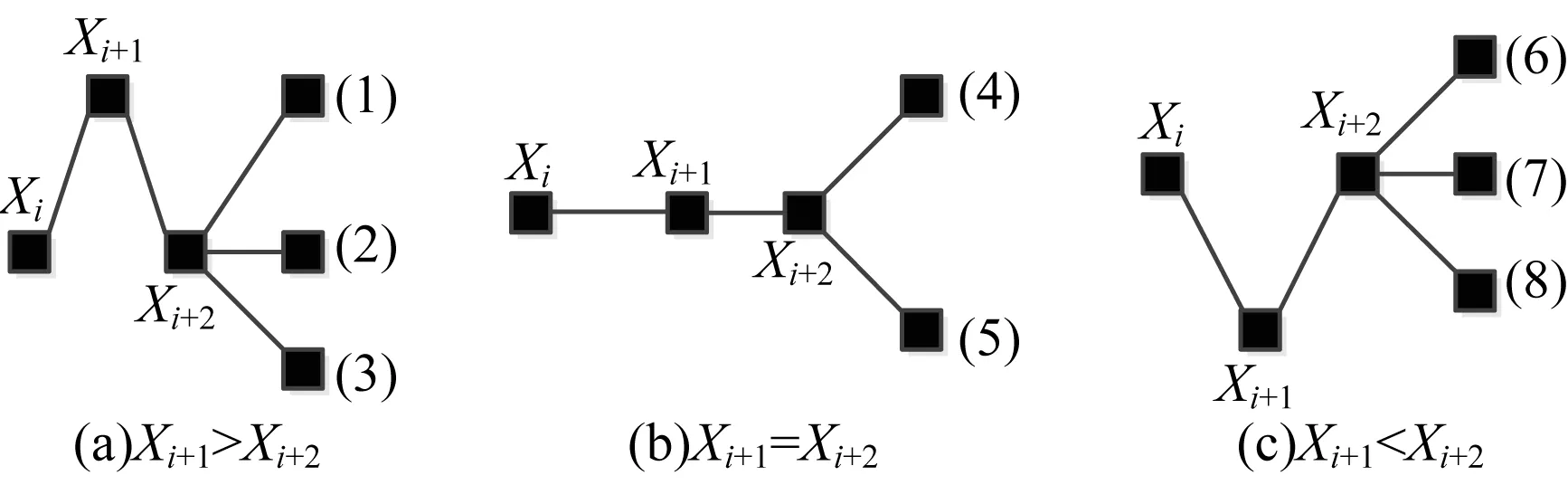
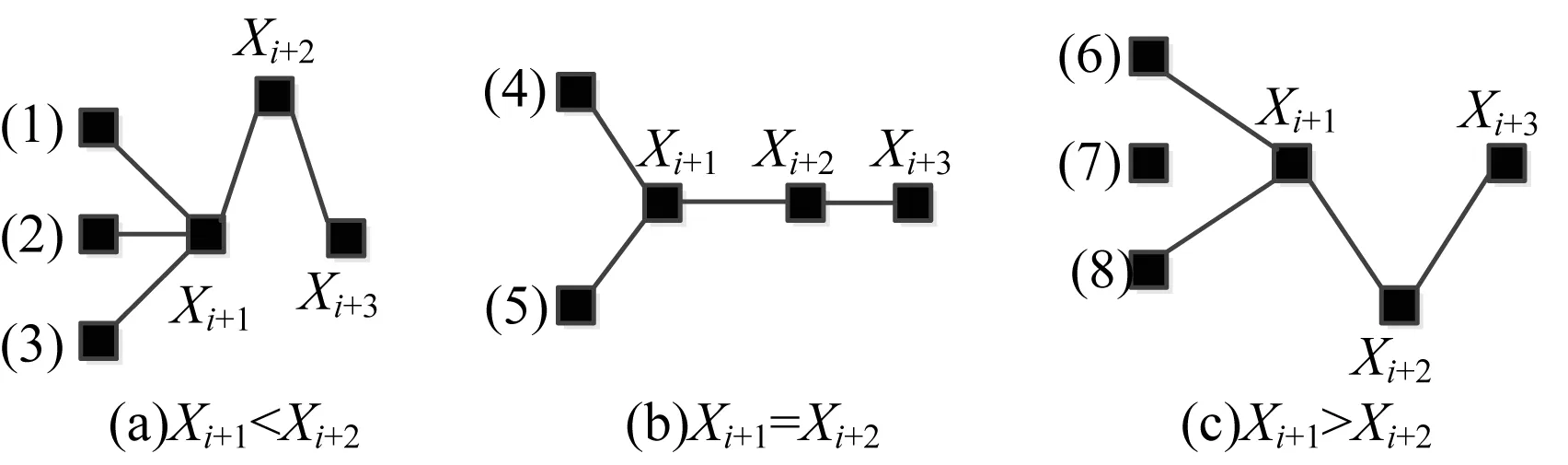
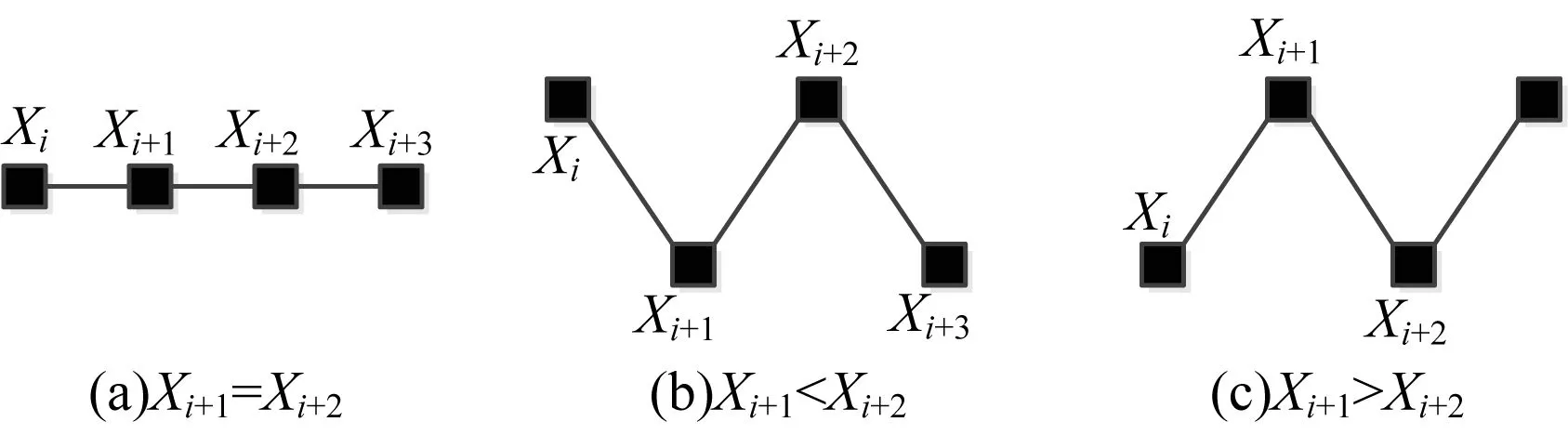
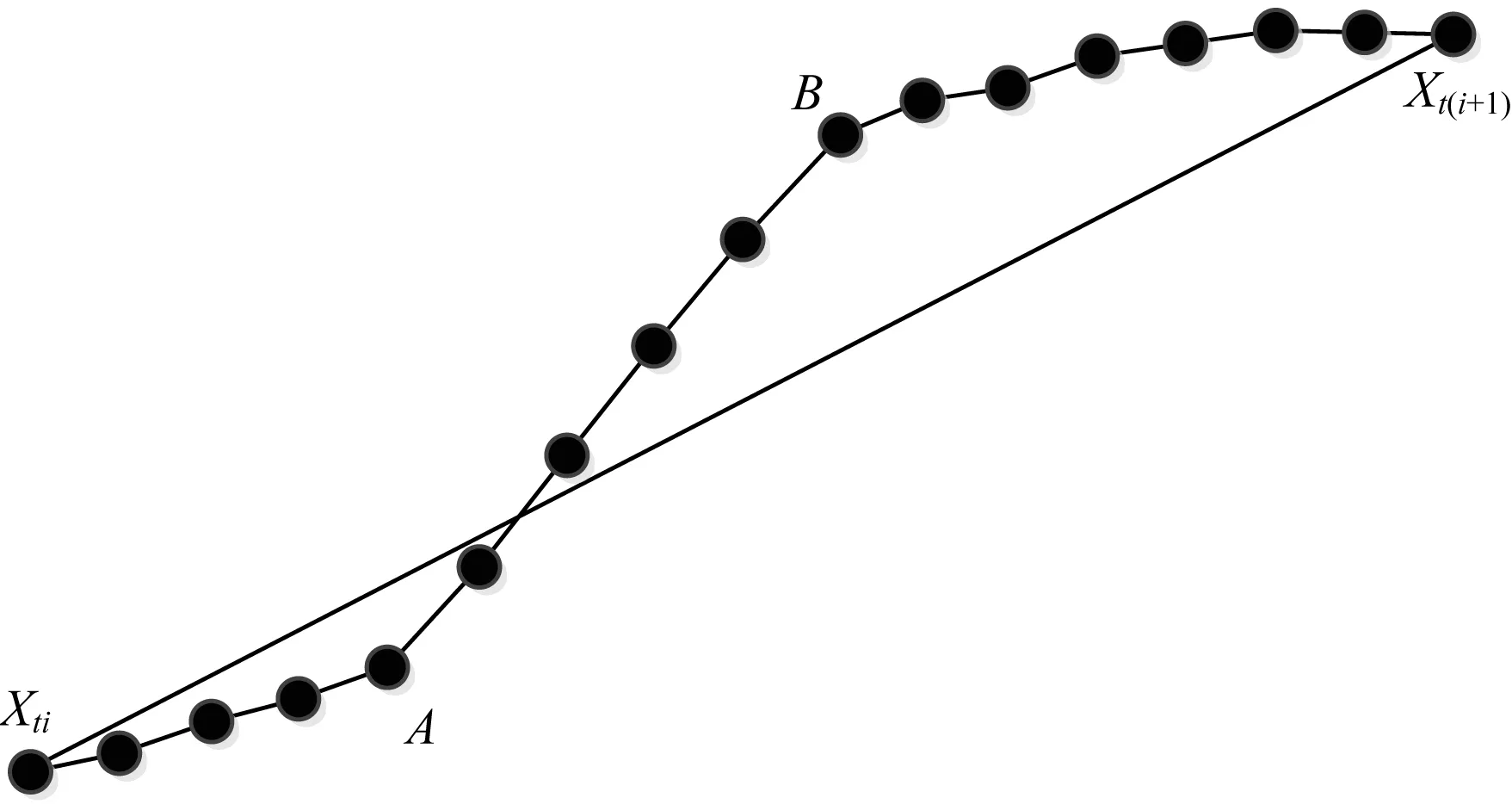
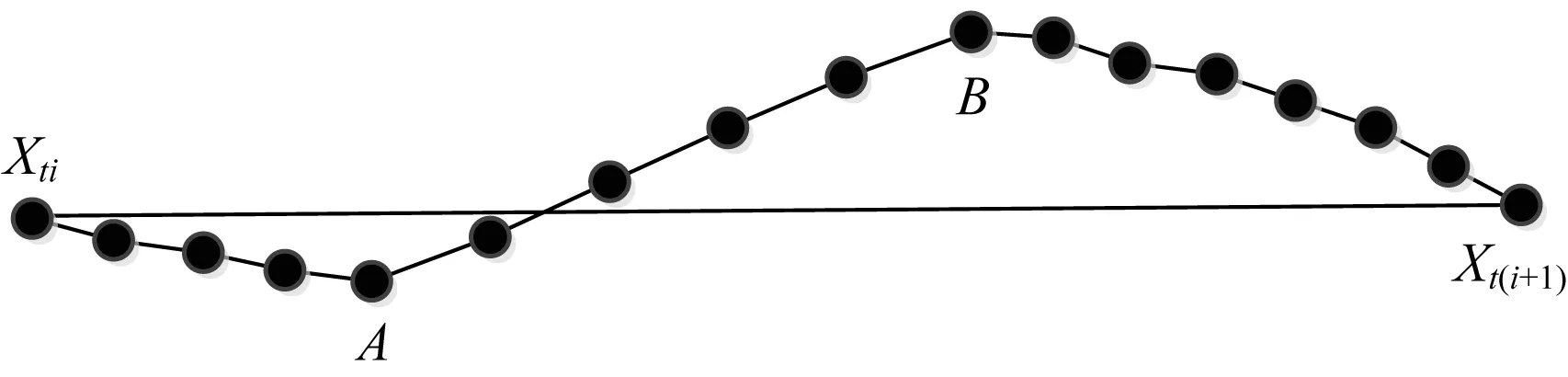
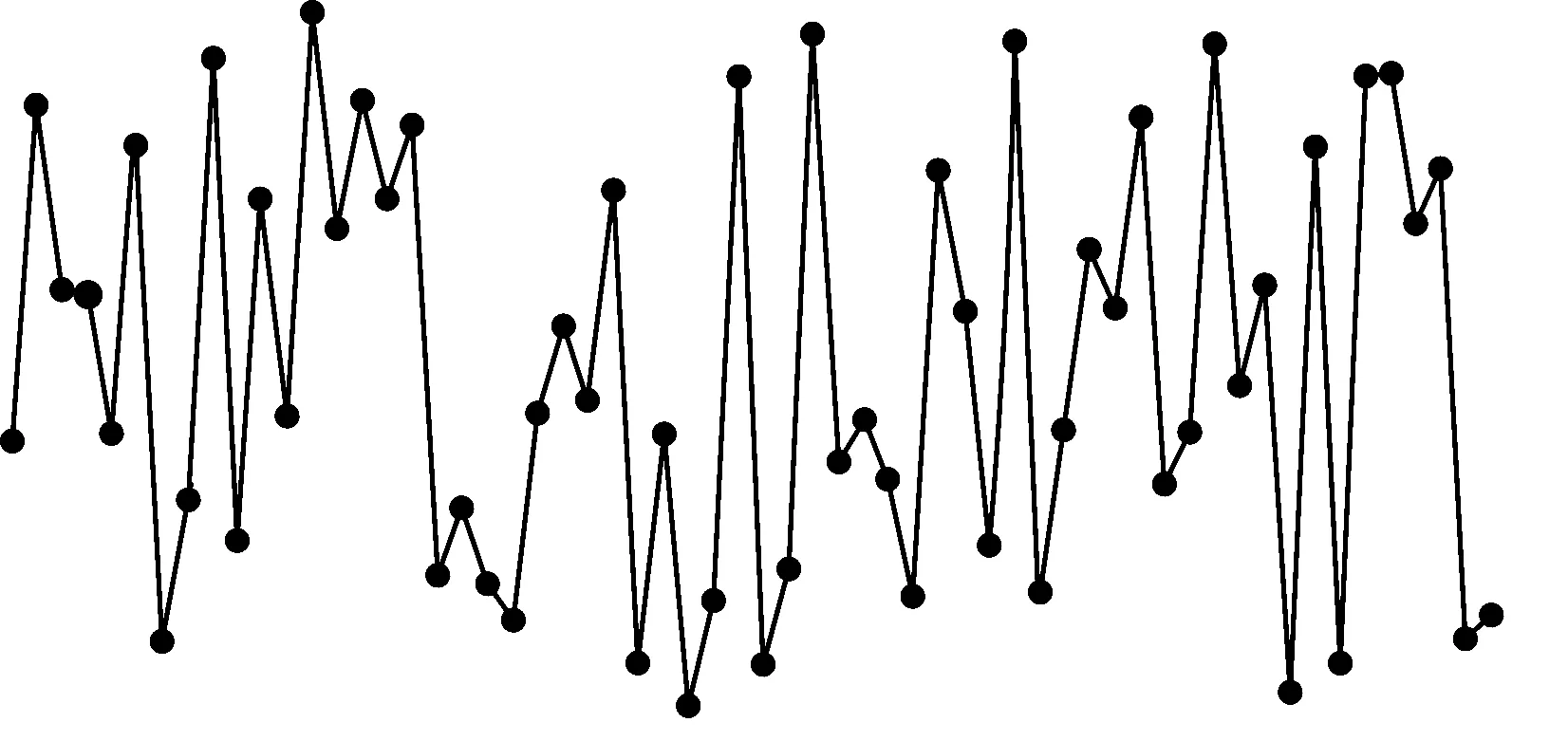
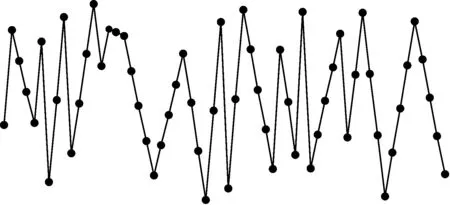
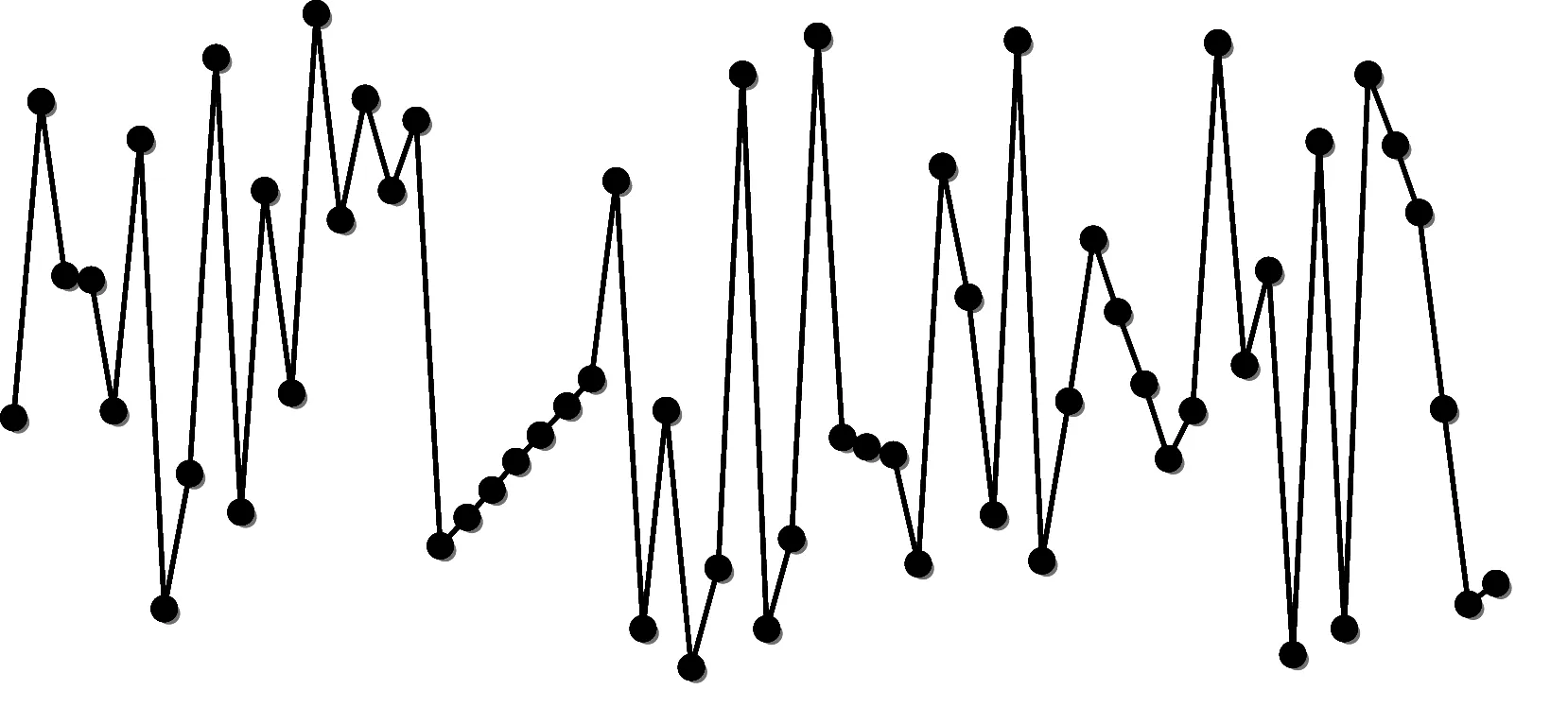
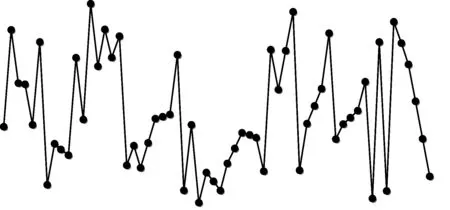
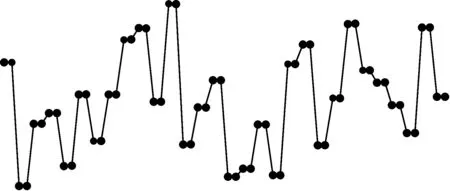
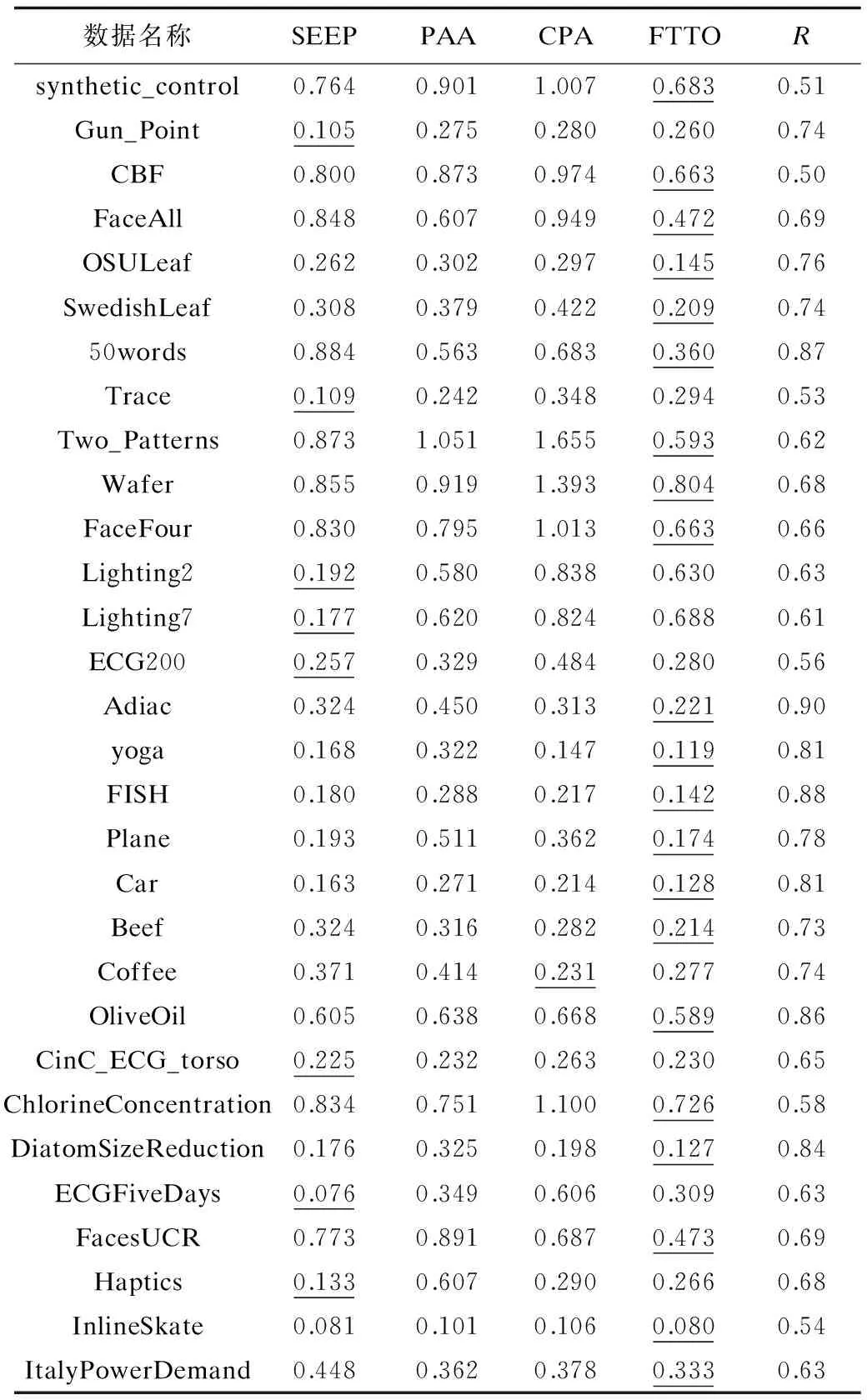
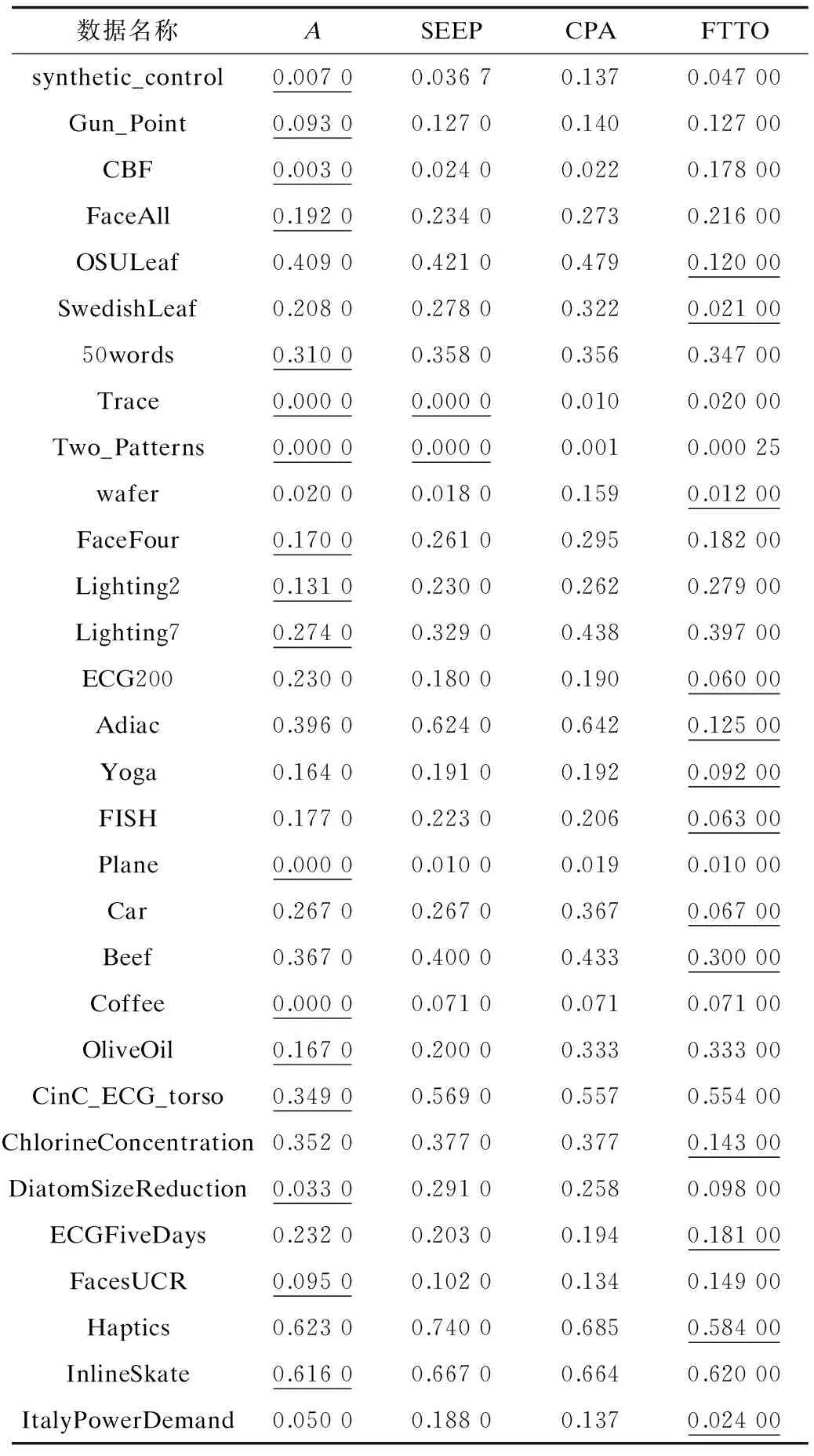
{(xi>xi+1)∪(xi≥xi+1)}{(xi≤xi+1)∪(xi {(xi (4) 定义6(基本趋势转折点) 时间序列数据的趋势可分为上升、平缓和下降3种基本趋势,根据这种趋势提取的转折点可以被称为基本趋势转折点。 定义7(拐点) 缓慢上升、快速上升、缓慢下降和快速下降属于在一个基本趋势中单位时间内数据的变化速率不同,依据变化速率不同提取的趋势转折点被称为拐点。 如图1所示[15],在时间序列中相邻3个数据点分别为xi、xi+1和xi+2,它们的发展趋势共有9种情况。当xi+2-xi>0时,即图1(a)、图1(b)、图1(e)这3种情况属于总体趋势上升。当xi+2-xi<0时,即图1(f)、图1(g)、图(i)这3种情况属于总体趋势下降。当xi+2-xi=0时,即图1(c)、图1(d)、图1(h)这3种情况属于总体保持不变。 图1 时间序列中相邻3点的变化趋势 在时间序列X中相邻的4个数据点分别为xi、xi+1、xi+2、xi+3,令: (xi+2-xi)×(xi+3-xi+1)=P (8) 当P大于零时,在相邻的4个数据点中,前3个数据点与后3个数据点趋势相同。当P小于零时,在相邻的4个数据点中前后趋势不同,出现趋势转折点。当P等于零时,相邻的4个数据点中前后趋势可能不同。下面分别讨论P小于、等于零的情况。 1)当P小于零时,(xi+2-xi)>0且(xi+3-xi+1)<0,前3点为上升趋势,分别对应图1(a)、图1(b)、图1(e)这3种情况,后3点为下降趋势。此时4个相邻数据点共有3种分布情况,如图2所示。依据定义4,趋势转折点是局部极值点,当上升趋势转变为下降趋势时,趋势转折点应为局部极大值点,所以比较xi+1与xi+2的大小,最大值是趋势转折点,若相等,则取xi+1作为趋势转折点。 图2 4个相邻数据点上升转下降示意图 2)当P小于零时,(xi+2-xi)<0、(xi+2-xi)>0、(xi+2-xi)<0且(xi+3-xi+1)>0,前3点为下降趋势,分别对应图1(f)、图1(g)和图1(i)3种情况,后3点为上升趋势。此时4个相邻数据点共有3种分布情况,如图3所示。同理,比较xi+1与xi+2的大小,下降趋势转变为上升趋势,所以局部极小值点是趋势转折点。若相等,取xi+1作为趋势转折点。 图3 4个相邻数据点下降转上升示意图 3)当P等于零时,(xi+2-xi)=0且(xi+3-xi+1)≠0,前3点趋势为保持不变,后3点趋势并不确定,如图4所示,后3点的变化趋势共有8种情况。由图4可知,xi+2是2种不同趋势变化交点,即取xi+2作为趋势转折点。 图4 4个相邻数据点保持转变化示意图 4)当P等于零时,(xi+2-xi)≠0且(xi+3-xi+1)=0,前3点趋势并不确定,后3点趋势为保持不变,如图5所示,前3点的变化趋势共有8种情况。由图5可以发现,xi+1是2种不同趋势的变化交点,即取xi+1作为趋势转折点。 图5 4个相邻数据点变化转保持示意图 5)当P等于零时,(xi+2-xi)=0且(xi+3-xi+1)=0,前3点与后3点的趋势相同保持不变,如图6所示,共有3种情况,趋势均视为平缓,所以此时无趋势转折点。 图6 4个相邻数据点趋势保持不变示意图 以上5种情况如表1、表2所示。 表1 当P<0时的情况 表2 当P=0时的情况 对原始时间序列数据使用以上算法可以得到3种基本趋势转折点。利用3种基本趋势转折点还原数据。为减少拟合误差,提高拟合精度,定义阈值Q,Q代表相邻2个趋势转折点的距离,即ti-t(i-1),当趋势转折点与前一个转折点间的距离大于Q时,提取拐点。 假设相邻2个基本趋势转折点为xti和xt(i+1),2个趋势转折点间的数据如图7所示,图7中共有A和B2个拐点。 图7 坐标转换前原始数据示意图 首先连接相邻的2个趋势转折点xti和xt(i+1),以连线作为X轴。其次将2个趋势转折点之间的原始数据与连线的距离作为新的时间序列数据,如图8所示。经过坐标旋转变换后,将缓慢上升、快速上升、缓慢下降和快速下降等拐点的提取问题转换为基本趋势转折点提取问题。最后对新的时间序列数据采用FTTO算法便可提取拐点。因为FTTO算法运算使用相邻的4个数据点,所以距离阈值Q应不小于5。 图8 坐标旋转转换后数据示意图 依据2.1节与2.2节提出的趋势转折点提取算法,实现FTTO算法共分为主函数和FTTO方法2个部分,如果需要提取拐点减少拟合误差,则添加FTTO-G方法部分。 主函数方法描述如下: 输入时间序列X={x1,x2,…,xn} Begin Xc={}{};/*实例化一个序列,存储趋势转折点*/ fi=0;/*保存前一个趋势转折点时间索引*/ se=0;/*保存当前趋势转折点时间索引*/ Xc.add(x1)/*数据起始点默认为趋势转折点*/ for(i=1;i /*遍历原始数据,相邻4个点计算P值*/ (xi+2-xi)×(xi+3-xi+1)=P /*依据FTTO算法,判断是否存在趋势转折点*/ FTTO(P,xi,xi+1,xi+2,xi+3) /*如果需要提取拐点,则根据输入的Q值和相邻2个转折点间距离判断是否使用FTTO-G算法*/ if(se-fi>Q) FTTO-G(fi,se); /*在提取拐点后,更新fi坐标索引*/ fi=se; Xc.add(xn) End FTTO方法描述如下: 输入P和相邻的4个数据点xi+1、xi+2、xi+3和xi+4 输出如果输入数据中存在趋势转折点,则Xc集合中添加转折点,如果输入数据中不存在趋势转折点,则不向Xc中添加数据 Begin if(P<0) if(xi+1≥xi+2) Xc.add(xi+1);se=i+1; else if(xi+1 Xc.add(xi+2);se=i+2; else if(xi+3-xi+1>0) if(xi+1>xi+2) Xc.add(xi+2);se=i+2 else if(xi+1≤xi+2) Xc.add(xi+1);se=i+1; else if(p=0) if((xi+3-xi+1) ≠0&& (xi+2-xi)=0)) Xc.add(xi+2);se=i+2; else if((xi+3-xi)=0 && (xi+2-xi)≠0)Xc.add(xi+1);se=i+1; End FTTO-G方法描述如下: 输入前一个趋势转折点时间坐标索引fi,当前趋势转折点时间坐标索引se 输出如果相邻2个趋势转折点之间存在拐点,则向Xc中添加数据,如果相邻2个趋势转折点之间不存在拐点,则Xc中数据不变 Begin G={};/*实例存储新的时间序列数据的序列*/ Calclinearequation();/*计算2个转折点间的直线方程*/ for(int?w=fi;w<=se;w++) G.add(distance(xw));/*计算每个点到直线的距离,并添加到G中*/ for(int??j=0;j /*对新的时间序列数据G,采用FTTO算法,将提取的趋势转折点添加到XC中*/ (Gj+2-Gj)×(Gji+3-Gj+1)=P FTTO(P,Gj,Gj+1,Gj+2,Gj+3) End 本文提出的FTTO算法时间复杂度为O(6n)。在程序运行过程中,首先需要遍历原始数据,计算相邻的4个数据点的值P,之后通过3次判断得出该算法是否存在趋势转折点。那么,此时的时间复杂度T1(n)=O((1+3)×(n-3))=O(4n)。如果需要提取拐点,则增加FTTO-G方法部分。首先计算相邻2个趋势转折点间直线方程的斜率与截距。之后遍历相邻2个趋势转折点间数据,形成新的时间序列数据,此时的时候复杂度T2(n)=O(n)。最后对新的时间序列数据使用FTTO算法。此时的时间复杂度T3(n)=O(n)。所以,FTTO算法的时间复杂度为O(4n+n+n)=O(6n)。 在提取基本趋势转折点过程中,FTTO算法将相邻的3个数据点作为基本趋势单元,不依赖任何先验知识,自动提取数据中基本趋势转折点。在提取拐点过程中,增加相邻2个基本趋势转折点间的距离阈值Q,对经过坐标变换后的数据使用FTTO算法提取拐点,从而提高拟合精度。 本文实验数据采用美国加州大学河滨分校收集整理的UCR时间序列分类数据集[17]。选择SEEP[13]、PAA[11]、CPA[16]算法与本文提出的FTTO算法进行对比,使用不同算法提取数据点分段线性表示原始数据,之后对比拟合误差。拟合误差越小,证明算法拟合性能越优秀。 在下文实验中,由于数据集中数据来自不同领域,首先进行数据归一化处理,数据归一化公式如下: (5) 文献[13]提出的SEEP算法是基于斜率提取数据点的代表性算法。首先计算连接同一点的左右两条线段的斜率。之后对比斜率的变化量是否超出阈值d,若大于阈值d,则提取分段点。最终连接分段点得到原始数据的分段线性表示。 文献[11]提出的PAA算法是分段线性表示的经典算法。首先使用等宽窗口划分原始数据,之后每个窗口内使用平均值代替原始数据,最后得到原始数据的分段线性表示。 文献[16]提出的CPA算法在提取分段点过程中具有良好效果。首先依据各个数据点在局部范围内的偏离程度定义了时间序列数据的变化点,之后连接每一个变化点,最后得到原始数据的分段线性表示。 以synthetic_control数据集中的第一条数据为例,比较4种算法的拟合效果。图9~图13分别为归一化原始数据、FTTO算法拟合数据、SEEP算法拟合数据、CPA算法拟合数据和PAA算法拟合数据效果示意图。 图9 原始数据效果示意图 图10 本文算法FTTO拟合数据效果示意图 图11 SEEP算法拟合数据效果示意图 图12 CPA算法拟合数据效果示意图 图13 PAA算法拟合数据效果示意图 从图9~图13对比结果可以看出,本文提出的FTTO算法能够提取数据主要趋势转折点达到保留原始数据的趋势信息的目的。SEEP与CPA算法均存在遗漏提取分段点的情况,PAA算法虽然保存了原始信息的整体趋势特征,但是丢失了每个窗口内的趋势信息。 4种算法在相同压缩率情况下拟合误差对比实验结果如表3所示,表3中R表示压缩率,FTTO算法提取拐点的阈值Q等于5。由于PAA算法的自身特点,实验过程中PAA算法压缩率大于且最接近表3中的压缩率。表3中下划线表示每行拟合误差最小值。 表3 拟合误差对比结果 从表3可以看出, 在30组时间序列数据中,SEEP算法在8类时间序列数据中拟合误差最小,CPA算法在1类时间序列数据中拟合误差最小,本文提出的FTTO算法在21类时间序列数据中拟合误差最小。 Keogh团队公布了在UCR时间序列分类数据集上,使用DTW算法在采用1-NN分类的情况下各个数据集的分类错误率。本文运用SEEP、CPA和FTTO算法对比拟合时间序列数据在采用1-NN分类和DTW距离度量情况下的分类错误率。对比结果如表4所示。在表4中,A列是Keogh团队公布的在原始数据上的分类错误率。各个数据的压缩率同表3中各个数据的压缩率相等。表4中下划线代表各行中的最小数据。 表4 UCR数据集对比分类结果 在表4中,有17组数据显示使用原始数据得到的分类错误率最小,使用SEEP算法有2组数据的分类错误率同原始数据相同达到最小,使用本文提出的FTTO算法在13组数据中分类错误率最小。并且Keogh团队公布的使用原始时间序列数据的分类错误率平均值为0.209 2,使用SEEP算法获得的分类错误率平均值为0.254 0,使用CPA算法获得的分类错误率平均值为0.273 7,使用本文提出的算法FTTO获得的分类错误率平均值为0.175 4,平均分类错误率达到最小。平均分类错误率相比原始数据的平均分类错误率下降0.033 9,整体分类错误率明显下降。 依据趋势转折点在时间序列数据中的重要特征,本文提出一种基于数据自身趋势特征提取数据转折点的算法(FTTO)。该算法计算简单,易于实现。通过在UCR时间序列分类数据集上与SEEP、CAP和PAA算法对比实验可以看出,该算法在还原原始序列数据时的拟合误差较小,具有去除干扰噪音数据的功能。实验结果表明,采用1-NN分类和DTW算法,与SEEP、CAP算法拟合的数据和Keogh团队公布的原始数据分类错误率相比,FTTO算法整体分类错误率最小。 [1] ESLING P,AGON C.Time-series Data Mining[J].ACM Computing Surveys,2012,45(1):11-12. [2] HU Zhikun,XU Fei,GUI Weihua,et al.Wavelet Matrix Transform for Time-series Similarity Measurement[J].Journal of Central South University of Technology,2009,16(5):802-806. [3] AGRWAL R,FALOUTSOS C,SWAMI A.Efficient Similarity Search in Sequence Databases[C]//Proceedings of the 4th International Conference on Foundations of Data Organization and Algorithms.London,UK:Springer-Verlag,1993:69-84. [4] RAFIEI D,MENDELZON A O.Querying Time Series Data Based on Similarity[J].IEEE Transactions on Knowledge & Data Engineering,2000,12(5):675-693. [5] REN J M.Similarity Search over Time Series Data Using Wavelets[C]//Proceedings of the 18th International Conference on Data Engineering.San Jose,USA:IEEE Computer Society Press,2002:212-221. [6] CHAN K,FU A.Efficient Time Series Matching by Wavelets[C]//Proceedings of the 15th IEEE International Conference on Data Engineering.Washington D.C.,USA:IEEE Press,1999:126-133. [7] KEOGH E J,CHU S,HART D,et al.An Online Algorithm for Segmenting Time Series[C]//Proceedings of IEEE International Conference on Data Mining.Washington D.C.,USA:IEEE Press,2002:289-298. [8] KEOGH E.Exact Indexing of Dynamic Time Warping[C]//Proceedings of the 28th International Conference on Very Large Databases.Hong Kong,China:[s.n.],2002:406-417. [9] 潘 定,沈钧毅.时态数据挖掘的相似性发现技术[J].软件学报,2007,18(2):246-258. [10] YI B K,FALOUTSOS C.Fast Time Sequence Indexing for Arbitrary LP Norms[C]//Proceedings of the 26th International Conference on Very Large Data Bases.[S.1.]:Morgan Kaufmann Publishers Inc.,2000:385-394. [11] KEOGH E,CHAKRABARTI K,PAZZANI M,et al.Dimensionality Reduction for fast Similarity Search in Large Time Series Databases[J].Journal of Knowledge and Information System,2001,3(3):263-286. [12] PRAT K B,FINK E.Search for Patterns in Compressed Time Series[J].International Journal of Image and Graphics,2002,2(1):89-106. [13] 詹艳艳,徐荣聪,陈晓云.基于斜率提取边缘点的时间序列分段线性表示方法[J].计算机科学,2006,33(11):139-142. [14] 林 意,王智博.基于一阶滤波的时间序列分段线性表示方法[J].计算机工程,2016,42(9):151-157. [15] 周大镯,李敏强.基于序列重要点的时间序列分割[J].计算机工程,2008,34(23):14-16. [16] 张 娜,李莉娟.时间序列分段线性表示的几种算法比较[J].中国西部科技,2009(14):80-81. [17] CHEN Yanping,KEOGH E.UCR Time Series Classification Archive[EB/OL].[2016-08-07].http://www.cs.ucr.edu/~eamonn/time_series_data/.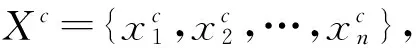
2 趋势转折点提取算法与分析
2.1 提取趋势转折点算法



2.2 拐点提取
2.3 算法实现步骤
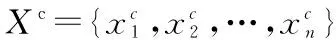
3 对比实验
3.1 对比拟合误差
3.2 对比分类错误率
4 结束语
