认知协作无线电网络下基于能效的资源联合分配

, ,品章

(重庆邮电大学 通信与信息工程学院,重庆 400065)

0 概述

在认知协作无线电网络(Cognitive Cooperative Radio Network,CCRN)中,将拥有频谱资源的授权系统称为主系统,共享主用户频谱资源的系统称为次级系统。认知用户不但要协助主用户传输信息,还要传输自己的数据。这样不仅可以提高主用户的传输质量,还可以让次用户获得传输的机会,以此来最大化利用资源。因此,通过在认知无线电网络中使用协作通信技术,可以达到双赢的效果[1-2]。

高数据速率业务的快速增长导致无线系统消耗大量的能量,节能成为当前非常紧迫的任务。在认知协作网络中,处于低优先级的认知系统在使用资源时,会受到很多限制,认知系统需要动态调整各项参数,而这将会对认知系统的性能产生影响,因此,如何合理地优化资源,使其在有限的资源条件下发挥最大效能,是认知协作网的重要研究问题。

过往人们考虑资源分配问题的主要目的是提高无线网络的系统性能[3-5],能效问题并没有引起人们足够的重视。文献[6]指出无线网络节点中的认知功能有效权衡能效和系统性能之间复杂的关系。文献[7]研究了协作频谱共享通信在保证主用户瞬时速率不变和次级用户服务质量的情况下最小化系统功率的问题。文献[8]分析了能效和频谱效率的折中问题,证明能效是关于频谱效率的凸函数。文献[9]求出了在最大化次系统能效下,允许接入频谱的次用户数目范围。文献[10-11]提出了低复杂度的基于能量效率的资源分配。文献[12]在满足整个系统的基本性能情况下,通过最小化能量消耗,对其资源进行优化。

本文基于次用户和定义的交易能效,提出次用户可以选择有利于自己系统能效的主用户的低复杂度机制,并对其频谱和功率进行联合优化,从而提高次系统的能效。

1 系统模型和问题描述

1.1 系统模型

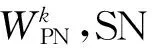
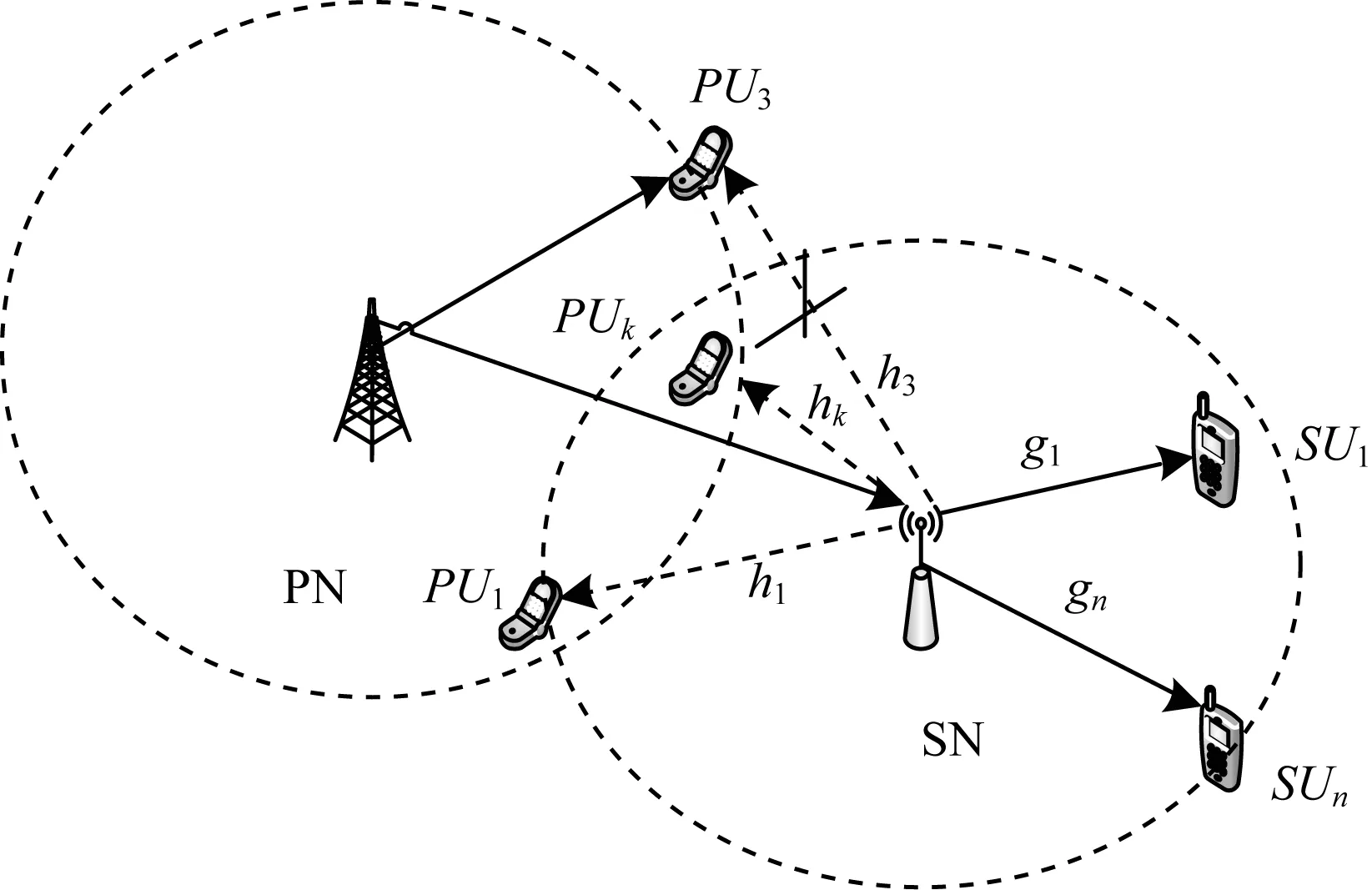
图1 系统模型

PN中边缘用户PUk(∀k∈K)接受协助后所达到的传输速率为:

(1)

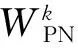
SN中的SUn的传输速率为:

(2)

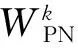
因此,SUn所达到的总速率为:

(3)

其中,xk∈{0,1}表示SNC是否协助PUk,如果协助,xk=1,否则xk=0。

整个SN所有SUS所达到的速率为:

(4)

SN中所消耗的功率包括协助转发PU的功率和传输自己数据所消耗的功率,为:

(5)

1.2 问题描述

综合考虑吞吐量与发射功率的关系,设计出一种SN系统能效最大化的分配方案。该方案SNC从PN中选择出能提高SN的系统能效的PUk进行协助,将其换取的带宽合理地分配给SUS,从而最终提高SN的能效。在认知协作网的通信系统中,能效定义为单位发射功率的吞吐量,因此定义SN的能效为:

(6)

SN系统能效最大化问题可以描述为如下约束条件的最大化问题,其中S为{{xk},{bk,n},{wk},{pk,n},{qk}}最佳资源分配 。

s.t.

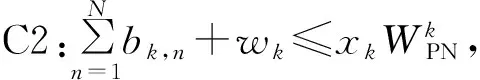
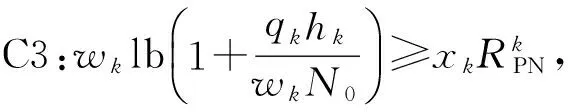
C5:xk∈{0,1},∀k∈K

C6:bk,n≥0,wk≥0,∀k∈K,n∈N

C7:pk,n≥0,qk≥0,∀k∈K,n∈N

(7)

定理1问题7等价于下述问题,其中S*为{{xk},{bk,k*},{wk},{pk,k*},{qk}}。

s.t.

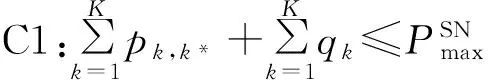
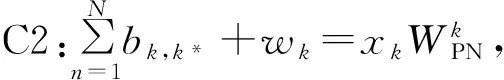
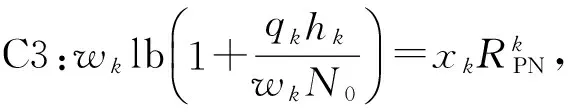
(8)

C5、C6、C7同式(7)。

其中,k*=argmaxn∈Ngk,n。

由定理1可知,如果SNC决定协助PUk,能效最高的方案是PUk的带宽最多由一个SUn共享。

(9)

(10)

通过式(9)、式(10)可以推出SN协助PUm所获得回报,即产生的速率:

(11)

2 确定PU下的能效优化

假设φ为由SN协助的PUS集合,即φ={k/xk=1,k∈K}。因此,对于给定的φ,式(8)将变为带宽和功率的联合分配,然而式(8)的目标函数为分数形式,将其重新写成:

(12)

其中,S为对应的解;π为C1～C4的可行域。

F(q)=maxS∈π{Rtotal(S)-qPtotal(S)}=0

(13)

其中,q为一个实参,对式(13)有下列3个性质:

性质1F(q)是关于q的单调递减。

性质2F(q)=0有唯一解。

性质3当且仅当:

F(q*)=maxS*∈π{Rtotal(S*)-q*Ptotal(S*)}=0

基于上述性质u,可以用搜索法求出q*。最优问题如下:

maxS∈πRtotal(S)-qPtotal(S)

(14)

对于此问题的求解可以用拉格朗日对偶算法。拉格朗日的对偶函数可以写为:

g(λ,μ)=maxS∈πL(pk,k*,wk,λ,μ)

L(pk,k*,wk,λ,μ)=

(15)

其中,λ、u为约束因子,则对偶最优化问题可以表述为:

ming(λ,u)

s.t.λ,u>0

(16)

式(16)可以采用次梯度求解,其中对偶变量的迭代更新过程如下:

(17)

(18)

其中,o(d)、κ(d)是迭代步长,d是迭代步数。

定理2给定λ,μ下,最佳资源分配如下:

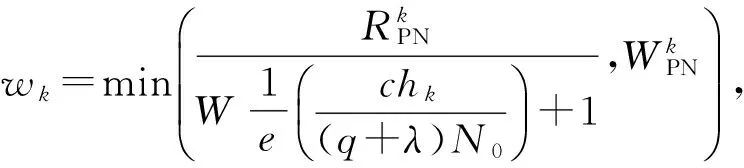
(19)

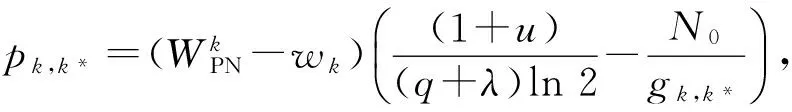
(20)

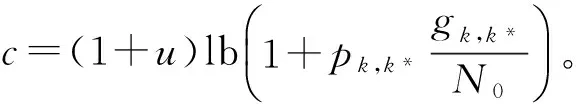
算法1

1.初始化精度δ和q=1;

2.循环:

3.初始化λ和μ;

4.循环:

5.由式(19)和式(20)计算出wk、pk,k*。

6.根据式(17)和式(18)更新λ和μ。

7.直到λ和μ收敛。

8.根据式(12)更新q。

9.直到|Rtotal(S)-qPtotal(S)|≤δ。

3 基于交易能效下PU的选择

3.1 交易能效的定义

本文提出了基于交易能效PU选择的方案,即集合φ的确定。首先,引入交易能效的概念,这个概念将在算法中起着关键作用,然后基于此,提出低复杂度的PU选择方案。

定义1交易能效:

(21)

其中,分子为SN共享PUk的带宽所获得的数据,分母为SUk*为了保证自身数据传输要求和协助PUk所消耗的功率。最大化交易能效的问题如下:

maxpk,k*≥0,wk≥0ηk=

(22)

式(22)利用KKT条件分别求关于pk,k*和wk的偏导,然后用二分法直到达到收敛,便可求出解。

3.2 集合φ的确定

定理3只有ηm>ηφ时,SN选择协助PUm才能提高SN的能效,其中m∈K,m∉φ。

证明:

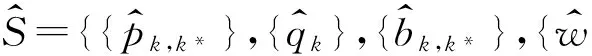
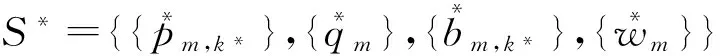
ηφ∪m=

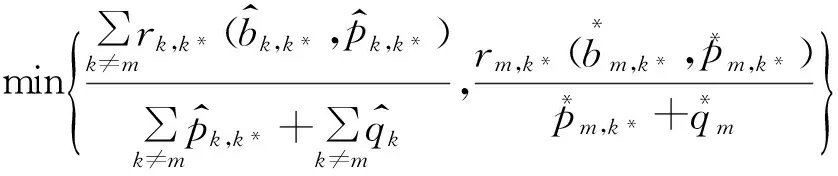
min{ηφ,ηm}

(23)

由式(23)可以看出,为了提高能效,即ηφ∪m>ηφ,必须ηm>ηφ,得证。

算法2

1.通过解决式(22)求出ηk,∀k。

2.将其交易能效ηk按降序的顺序排列,即:

η1>η2>…>ηk

3.初始化φ=Ø,并用算法1求出ηφ。

4.for k=1:K

用算法1求出ηφ∪k

if ηφ∪k>ηφ

φ=φ∪{k}

end

end

4 仿真结果与分析

本文利用Matlab对其进行仿真来验证合理性。考虑这样一个几何模型,主系统基站和次系统BS的距离为500 m,主系统和次系统覆盖半径分别为500 m和50 m。仿真参数设置如表1所示。

表1 仿真参数设置

将本文的仿真与参考文献[14-15]的方案作对比。

图2 能效随次系统最大功率约束的变化

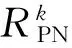
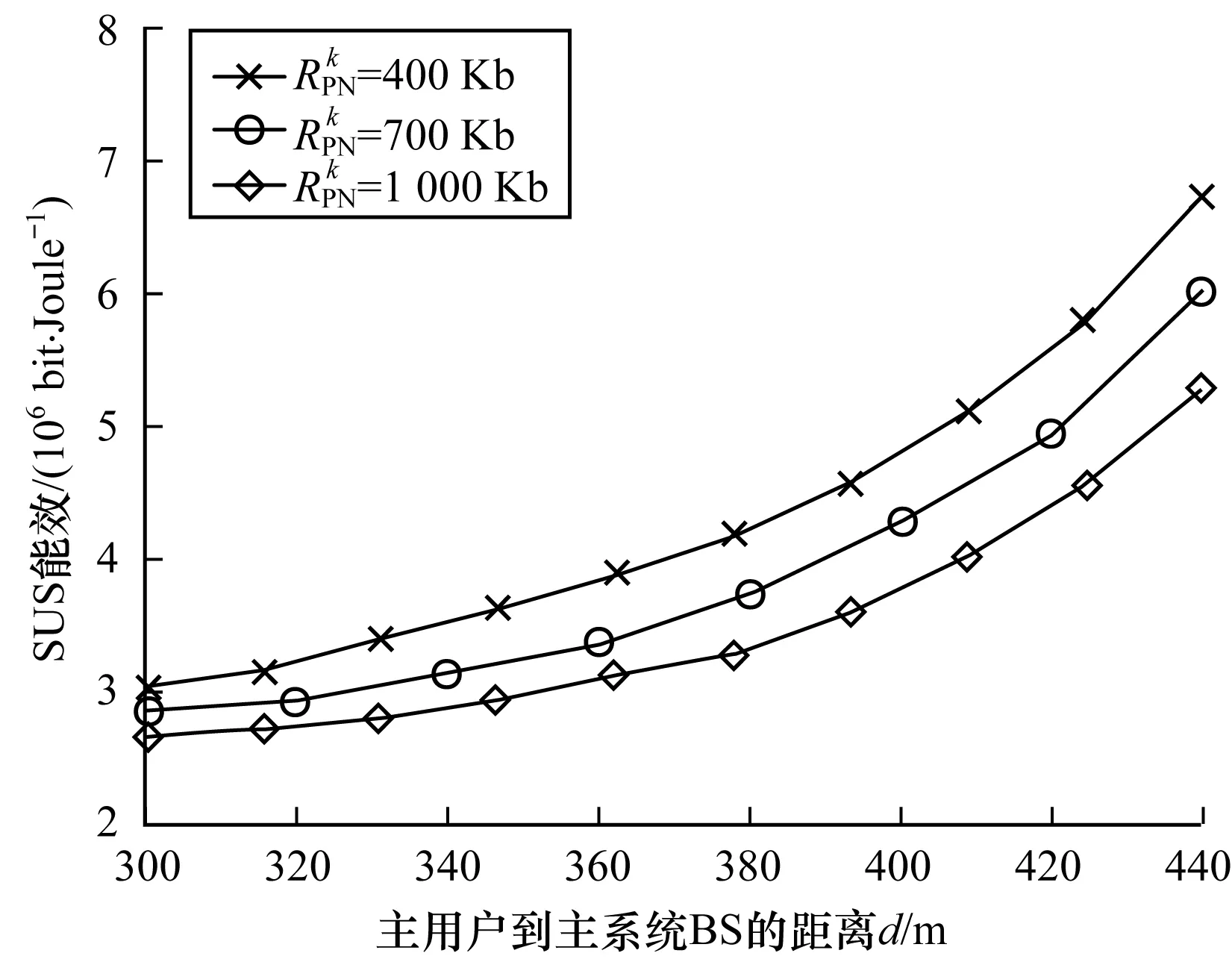
图3 能效随距离的变化

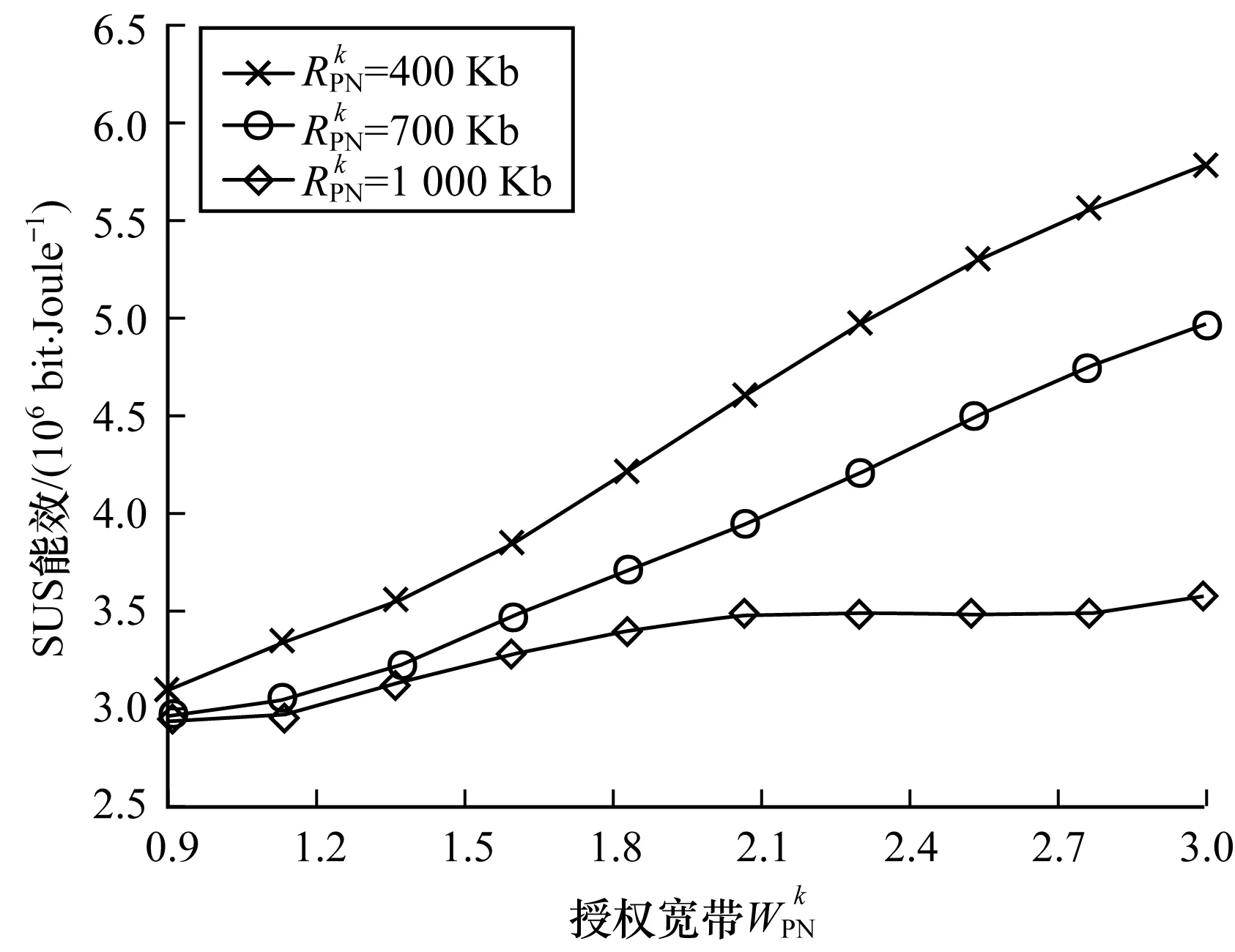
图4 能效随授权带宽的变化

5 结束语

本文探讨了认知协作网的频谱和功率交易,并对该系统进行建模分析,次用户可以选择有利于自己系统能效的主用户进行选择,并对其频谱和功率进行联合优化,即在满足主用户的基本要求下最大化次系统的能效,从而促使主用户和次用户之间进行合作。仿真结果证明,本文提出的资源分配方案可以在满足主用户基本性能的情况下,更好地提高次用户系统的能效。

[1] DOCKET E T.Spectrum Policy Task Force Report[J].Federal Communication Commission,2002,40(4):147-158.

[2] PHUYAL U,JHA S C,BHARGAVA V K.Green Resource Allocation with QoS Provisioning for Cooperative Cellular Network[J].Information Theory,2011,24(5):206-210.

[3] 王仕果,易 进.中继协作认知无线电系统的最优化功率分配[J].计算机工程,2015,41(5):93-96.

[4] ZHU Qionghua,WU Yuan.Cooperative Spectrum Sharing in Cognitive Radio Networks with Proactive Primary System[C]//Proceedings of IEEE International Conference on Communications in China-workshops.Washington D.C.,USA:IEEE Press,2013:82-87.

[5] NAMVAR N,AFGHAH F.Spectrum Sharing in Cooperative Cognitive Radio Networks:A Matching Game Framework[J].Information Theory,2015,62(5):1-5.

[6] GUR G,ALAGOZ S.Green Wireless Communications via Cognitive Dimension:An Overview[J].IEEE Network,2011,25(2):50-56.

[7] HE Jie,XU Chunlin,LI Liwei.Power Saving for Cooperative Spectrum Sharing-based Cognitive Radios Under Primary User Short-term Rate Protection[J].IET Communications,2012,6(9):1097-1103.

[8] 刘丹丹.高能效频谱共享协作通信机制研究[D].北京:北京邮电大学,2014.

[9] GAO Hongyuan,EJAZ W.Cooperative Wireless Energy Harvesting and Spectrum Sharing in 5G Networks[J].IEEE Access,2016,4(6):3647-3658.

[10] CHEN Jian,LÜ Lü,LIU Yiyang.Energy Efficient Relay Selection and Power Allocation for Cooperative Cognitive Radio Networks[J].IET Communications,2015,9(13):1661-1668.

[11] 郝万明.协作认知无线电网络中基于能效和谱效的资源分配技术研究[D].郑州:郑州大学,2015.

[12] LIU DANDAN,HUANG Cong.Resource Allocation in High Energy-efficient Cooperative Spectrum Sharing Communication Networks[J].Chinese Journal of Elec-tronics,2016,25(4):768-773.

[13] 张国坤.多元函数的凹凸性[J].曲靖师专学报,1999,9(1):10-14.

[14] RAMAMONJISON R,BHARGAVA V K.Energy Effi-ciency Maximization Framework in Cognitive Downlink Two-tier Networks[J].IEEE Transactions on Wireless Communications,2015,14(3):1468-1479.

[15] YONG S S,QUEK T Q S,KOUNTOURIS M.Energy Efficient Heterogeneous Cellular Networks[J].IEEE Journal on Selected Areas in Communications,2013,31(5):840-850.