全光逻辑与门转换效率的研究*

胡永倩，王海龙，张书玉，密术超，龚 谦

（1.山东省激光偏光与信息技术重点实验室，曲阜师范大学 物理系，山东 曲阜 273165；2.中国科学院上海微系统与信息技术研究所 信息功能材料国家重点实验室，上海 200050）

0 引 言

随着大数据时代的到来，传统的光纤网络已逐渐无法满足人们对信息传输速度和网络容量的要求[1]。应用全光网络实现的通信系统，由于信号的传输过程在光域[2]中进行，从而有效克服了传统网络中光-电-光转换带来的“电子瓶颈”[3]。全光网络与传统通信网络相比，具有集成性高﹑重组灵活﹑兼容性好等优点[4]，成为现代通信网络的发展趋势。在全光网络中，全光逻辑处理技术是实现信息交换的核心，而全光逻辑器件[5]因提高了带宽网络传输速率并进一步扩大了光网络的工作容量而被广泛应用。由于量子点半导体光放大器（QD-SOA）相比于其他类型的半导体光放大器（SOA）具有阈值电流低﹑噪声指数低﹑功耗低﹑更高的温度稳定性﹑饱和功率高以及超快的增益恢复特性等优点[6]，所以基于QD-SOA实现的全光逻辑器件成为研究热点之一。

如今已经实现的基于QD-SOA的全光逻辑器件大多运用了QD-SOA优异的非线性特性效应，包括交叉增益调制效应（XGM）﹑交叉相位调制效应（XPM）和四波混频效应（FWM)[7-8]。基于XGM效应实现的全光逻辑器件主要利用输入泵浦光脉冲的变化引起QD-SOA增益的变化，具有结构简单﹑转换效率高﹑输入功率动态范围大和容易实现等优点[9-10]。而基于QD-SOA的全光与门是全光逻辑门中较为核心的逻辑门，较多应用于全光解复用﹑全光加法器以及全光校验器[11]。

之前对基于XGM效应和XPM效应的全光波长转换器的转换效率进行了讨论[12]，本文在XGM效应的基础上，通过将两个QD-SOA级联来实现全光逻辑与门。着重讨论了脉冲宽度﹑损耗系数﹑有源区长度﹑电子从激发态（ES）到基态（GS）的跃迁时间以及最大模式增益对全光逻辑与门转换效率的影响，同时分析了全光逻辑与门转换过程中各参量与误码率之间的关系。研究结果表明，通过优化参量，可以在减小误码率的基础上，提高全光逻辑与门的转换效率。

1 基本原理

1.1 QD-SOA模型

图1为浸润层（Wetting Layer，WL）﹑激发态（Excited State，ES）和基态（Ground State，GS）所构成的量子点半导体光放大器（QD-SOA）的三能级结构[13]。

图1 QD-SOA能级结构

其中WL的载流子浓度变化以及电子在ES和GS的占有几率变化，可用三能级跃迁速率方程[14]表示为：

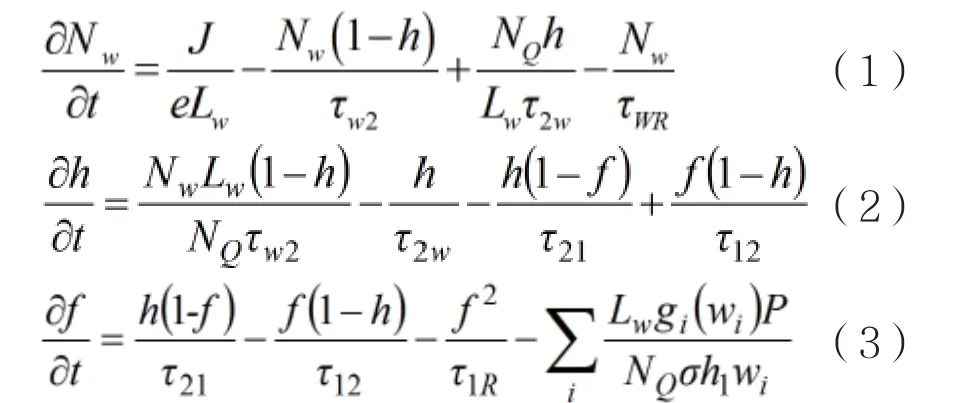
其中Nw表示WL中的载流子浓度，Lw﹑σ分别表示有源区厚度和有源区横截面积，J﹑e分别表示注入的电流密度和电子电量，h﹑f分别表示电子在GS和ES中的占有几率，τwR﹑τ1R分别表示电子在WL中的自发辐射时间和电子在量子点中的自发辐射时间，τ2W﹑τ21分别表示电子从ES到WL以及GS中的跃迁时间，电子从WL到ES的弛豫时间表示为τw2，电子从ES到GS的跃迁时间表示为τ12，h1wi表示光子能量，其中wi为光频率，h1为电子在ES中占有几率的初始值，gi表示第i段的模式增益。

假设QD-SOA的端面反射率为0，而且忽略ASE噪声，即QD-SOA处于理想状态时，输入光在QD-SOA中传输的光场方程[15]表示为：

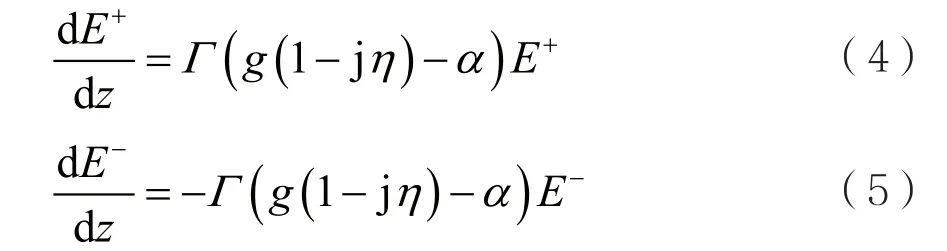
式（4）﹑式（5）中光场限制因子表示为Γ，z表示光场传输方向，E+﹑E-分别表示输入光沿z方向（﹢z）以及沿z的相反方向（﹣z）传播的光场强度，η﹑α分别表示线宽增强因子和波导损耗系数。

由式（6）和式（7）来表示光场传输方程的式（4）﹑式（5）的边界条件：

图2为QD-SOA细化分段模型[16]，首先将QD-SOA分成等长的M小段。当M足够大时，将各段中的载流子近似看作是均匀的，并将第j段内的载流子浓度记作Nj(t)。为了对每一段有源区内的载流子变化情况有更精确描述，将第j段再细化分成N段，此时将每一小段记作ΔL=L/(M×N)。

图2 QD-SOA细化分段模型

1.2 工作原理

如图3所示，在XGM的基础上，利用QDSOA1和QD-SOA2级联实现全光逻辑与门。

图3 基于QD-SOA-XGM的全光逻辑与门结构

波长为λ1的信号光DataA和波长为λ2的连续探测光通过一个3 dB耦合器注入到QD-SOA1中。当DataA为高电平“1”时，QD-SOA1有源区内的载流子发生受激辐射，导致载流子浓度下降，从而使得QD-SOA1的增益达到饱和，此时探测光没有被放大，输出为“0”；当DataA为低电平“0”时，QD-SOA1有源区内的载流子几乎没有发生受激辐射，载流子浓度几乎不受影响，此时探测光会获得较高的增益，因此探测光得到放大，输出为“1”。经过上述过程，在QD-SOA1输出端得到波长为λ2且与DataA波形反向的非信号DataA—。此后，将QD-SOA1的输出信号光DataA—和波长为λ3的信号光DataB同时输入到QD-SOA2中，此时DataA—的功率远大于DataB，因DataA—为强泵浦光，DataB为弱探测光，且QD-SOA2中的载流子浓度主要受DataA—影响：当DataA—为高电平“1”时，DataB无论是高电平“1”还是低电平“0”，都不能被放大，此时输出为“0”；当DataA—为低电平“0”时，DataB才能被QD-SOA2放大，其中当DataB为“1”时，输出为“1”；当DataB为“0”时，输出为“0”，从而实现全光逻辑与门。表1为逻辑与门的真值表。

表1 逻辑与门的真值表

在实现全光逻辑与门的过程中，输入信号DataA和DataB是脉冲宽度为2.0 ps的一阶高斯脉冲信号，DataA的波长λ1=1 550 nm，DataB的波长λ3=1 500 nm，探测光波长λ2=1 500 nm，取输入信号DataA的峰值功率为30 dBm，DataB的峰值功率为0 dBm。如图4所示，当输入信号DataA为1011001，DataB为1101101时，全光逻辑与门的运算结果为1001001。

图4 基于QD-SOA-XGM的全光逻辑与门运算结果

2 数值模拟

转换效率作为衡量波长转换系统的重要性能指标，控制着输入功率和输出功率的可变化范围。转换效率被定义为输出探测光的平均功率与输入泵浦光的平均功率之比：

下面将分别讨论有源区长度﹑电子从激发态（ES）到基态（GS）的跃迁时间﹑脉冲宽度﹑最大模式增益以及损耗系数对全光逻辑与门转换效率的影响。

2.1 脉冲宽度与转换效率的关系

图5显示了 不同脉冲宽度时测得的转换效率。由图5可知，脉冲宽度由0.5 ps增加至2.0 ps的过程中，转换效率由7.095 7 dB增至7.147 5 dB。这是由于脉冲宽度增加时，有源区内的载流子会更早发生受激辐射，且载流子消耗速率加快，从而使转换效率不断提高。

图5 脉冲宽度与转换光功率的关系

图6同时给出了脉冲宽度对误码率﹑转换效率的影响。

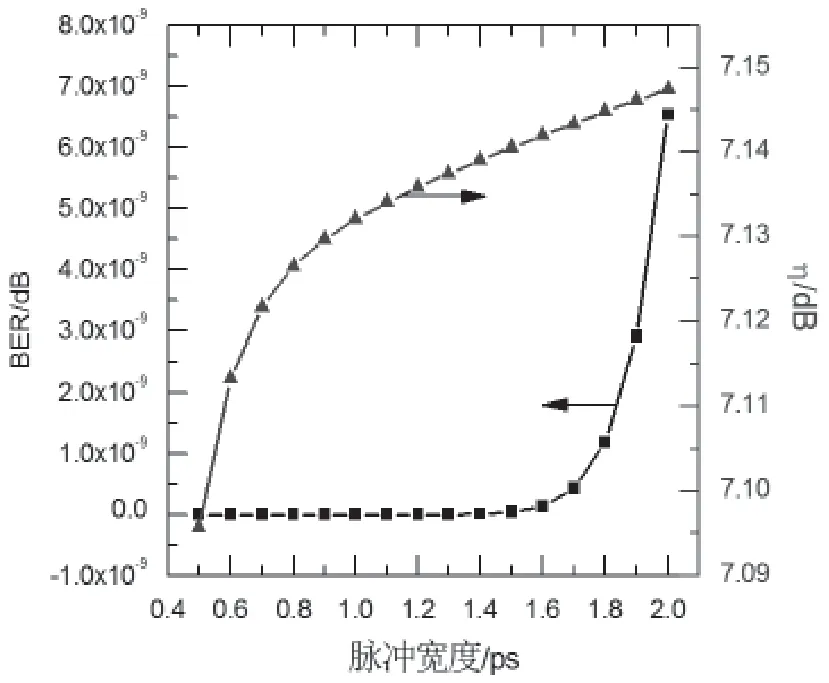
图6 误码率﹑转换效率随脉冲宽度的变化

当脉冲宽度为0.5 ps时，误码率为5.045 9×10-29；当脉冲宽度为1.2 ps时，误码率为2.339 6×10-13；当脉冲宽度为2.0 ps时，误码率为6.543 9×10-9。可见，随着脉冲宽度的增加，误码率增大，而转换效率随着脉冲宽度的增加而增大。因此，同时获得较高的转换效率和较低的误码率之间存在一定的矛盾性。所以，脉冲宽度的选取需适当，应该兼顾转换效率和误码率。

2.2 损耗系数与转换效率的关系

图7为损耗系数与转换效率的关系图。当损耗系数为340/m时，转换效率为6.496 4 dB；当损耗系数为260/m时，转换效率为6.803 4 dB；当损耗系数为180/m时，转换效率为7.147 5 dB。由此可知，转换效率随着损耗系数的减小而增大。这是因为随着损耗系数不断减小，信号光的损耗减小，使得有源区内的载流子发生受激辐射的概率增加，载流子浓度变化加快，从而引起转换效率增大。

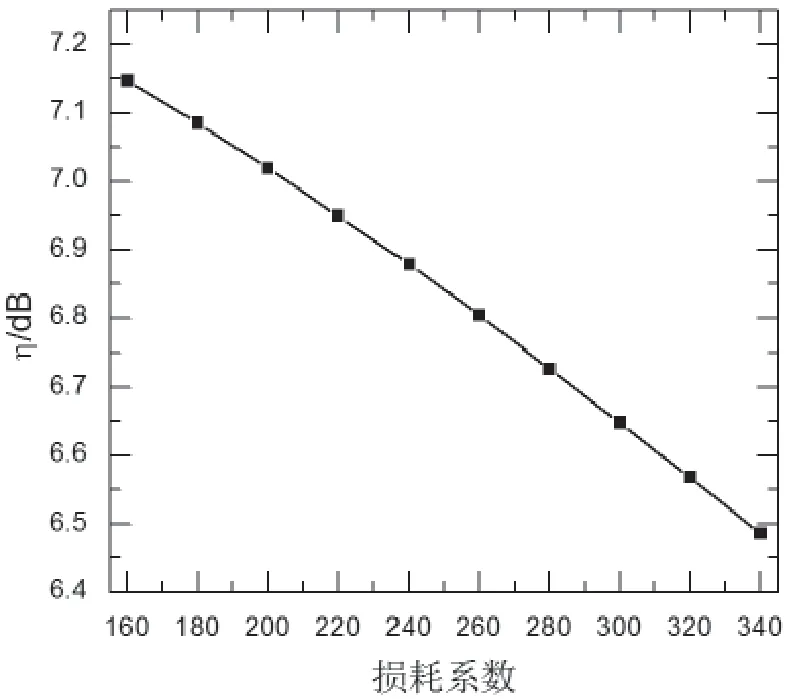
图7 损耗系数与转换效率的关系

图8同时显示了损耗系数对误码率﹑转换效率的影响。当损耗系数由340/m减小到160/m时，误码率由9.366 2×10-9减小至6.543 9×10-9。同时，随着损耗系数的减小，转换效率不断增大。综上所述，减小损耗系数可以提高全光逻辑与门的转换效率，同时减低误码率。

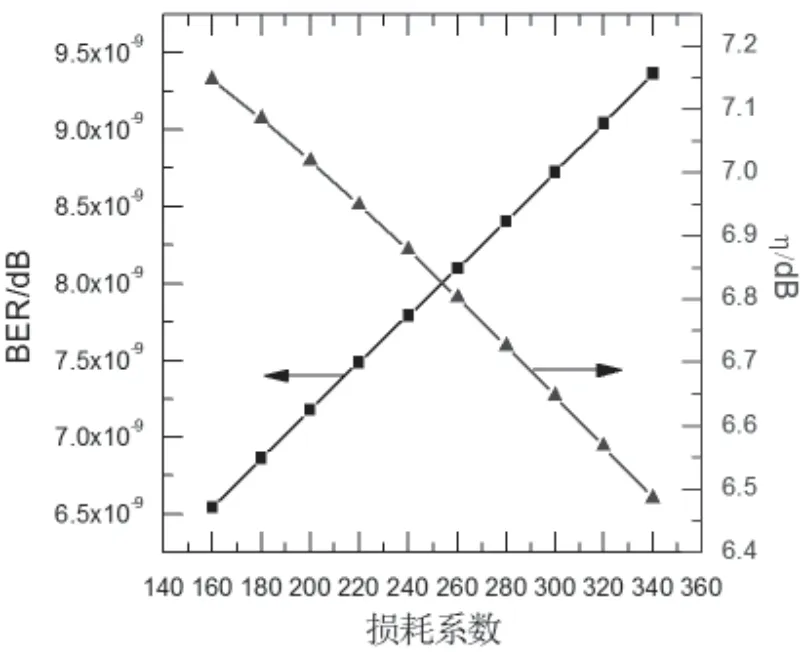
图8 误码率﹑转换效率随损耗系数的变化

2.3 有源区长度与转换效率的关系

如图9所示，当有源区长度为1.5 mm时，转换效率为0.597 2 dB；当有源区长度为2.0 mm时，转换效率为7.147 5 dB；当有源区长度为2.2 mm时，转换效率为4.405 5 dB。由此可知，随着有源区长度的增加，转换效率先增大后减小。这是因为有源区长度的增大使得输入信号被放大的几率增大，从而经过QD-SOA后产生的光增益增大，提高了探测光的放大倍数，使得转换效率不断提高。但是，由于增益饱和效应的存在，光信号功率的放大效果会减弱，使得转换效率不断降低。

图9 有源区长度与转换效率的关系

图10显示了有源区长度与误码率的关系，其中插图为有源区长度在1.9 mm至2.2 mm的误码率变化。由图10可知，当有源区长度为1.5 mm时，误码率为5.696 6×10-6；当有源区长度为1.9 mm时，误码率为8.681 1×10-9；当有源区长度为2.2 mm时，误码率为3.098 0×10-12。可见，随着有源区长度的增加，误码率不断减小。

图10 有源区长度与误码率的关系

图11同时给出了误码率和转换效率随着有源区长度的变化规律。由图11可知，当有源区长度小于2.0 mm时，增大有源区长度可以提高转换效率，同时减小误码率。但是，当有源区长度大于2.0 mm时，同时获得较高的转换效率和较低的误码率之间存在一定的矛盾性。综上所述，有源区长度的选取须适当，要同时兼顾转换效率和误码率。

图11 误码率﹑转换效率随有源区长度的变化

2.4 最大模式增益与转换效率的关系

图12中，当最大模式增益为1 500/m时，转换效率为1.511 6 dB；最大模式增益为2 100/m时，转换效率为3.486 7 dB；当最大模式增益为3 000/m时，转换效率为7.147 5 dB。可知，最大模式增益增加，光增益随之增大，QD-SOA有源区内载流子与输入光发生受激辐射的概率增大，且速率也会增加，导致载流子浓度快速变化，使得转换效率提高。

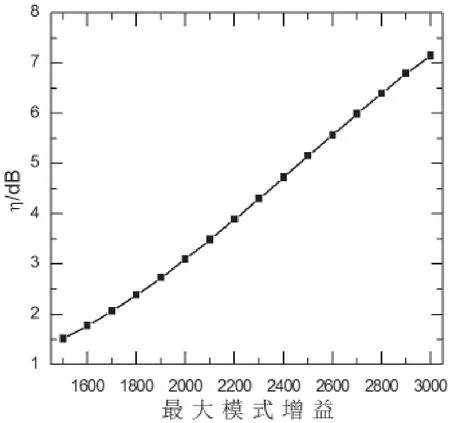
图12 最大模式增益与转换效率的关系

由图13可知，在最大模式增益由1 500/m增加至3 000/m的过程中，误码率由1.971 0×10-7减小至6.543 9×10-9。可见，误码率随着最大模式增益的增大而不断减小，同时转换效率随之提高。

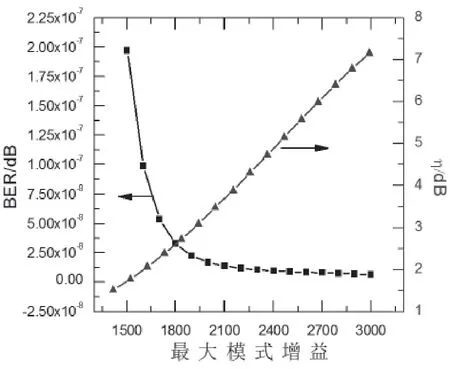
图13 误码率﹑转换效率随最大模式增益的变化

2.5 电子从ES到GS的跃迁时间与转换效率的关系

由图14可知，跃迁时间由1.28 ps减小至0.16 ps的过程中，转换效率由2.200 4 dB增加至7.147 5 dB。可见，随着跃迁时间的不断减小，此时基态被消耗的电子会得到及时补充，电子发生受激辐射的概率随之增加，因此转换效率不断提高。

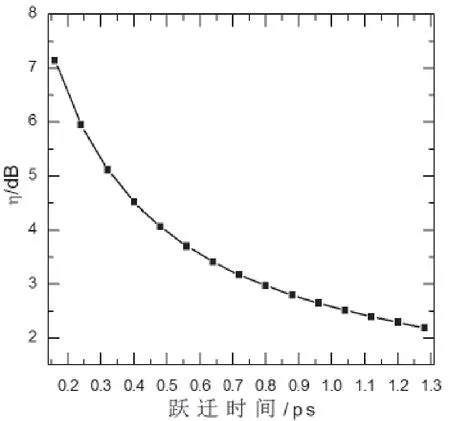
图14 电子从ES到GS跃迁时间与转换效率的关系

图15为误码率和转换效率与跃迁时间的关系。

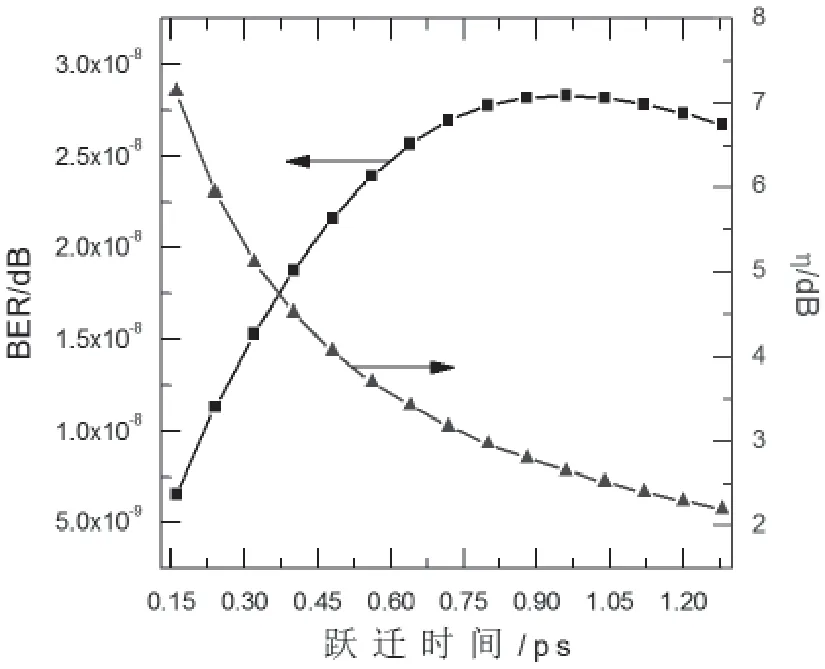
图15 误码率﹑转换效率随电子从ES到GS跃迁时间的变化

当跃迁时间为1.28 ps时，误码率为2.674 5×10-8；当跃迁时间为0.96 ps时，误码率为2.833 5×10-8；当跃迁时间为0.16 ps时，误码率为6.653 9×10-9。由此可知，随着跃迁时间的减小，误码率先增大后减小，同时转换效率不断增大。因此，电子从ES到GS的跃迁时间选取时须适当，应同时兼顾误码率和转换效率。

3 结 语

本文利用QD-SOA的交叉增益调制效应（XGM），通过两个QD-SOA的级联结构实现了全光逻辑与门，并详细分析了全光逻辑与门的转换效率和误码率。研究结果表明：全光逻辑与门的转换效率随着有源区长的增加先提高后降低，而增大脉冲宽度﹑最大模式增益以及减小损耗系数﹑电子从ES到GS的跃迁时间会使得全光逻辑与门的转换效率得到提高。通过优化参量，全光逻辑与门的转换效率由0.301 3 dB提高至7.147 5 dB。但是，有源区长度﹑脉冲宽度以及电子从ES到GS的跃迁时间的选取须适当，因为获得较高的转换效率和较低的误码率之间存在一定的矛盾。所以，选取参数时要兼顾转换效率和误码率，在减小误码率的基础上提高转换效率。

[1] Farmani A,Farhang M,Sheikhi M H.High Performance Polarization-independent Quantum Dot Semiconductor Optical Amplifier with 22dB Fiber to Fiber Gain Using Mode Propagation Tuning without Additional Polarization Controller[J].Optics & Laser Technology,2017(93):127-132.

[2] Arun V,Singh A K,Shukla N K,et al.Design and Performance Analysis of SOA-MZI based Reversible Toffoli and Irreversible AND Logic Gates in a Single Photonic Circuit[J].Optical and Quantum Electronics,2016,48(09):445.

[3] Matsuura M,Ohta H,Seki R.Experimental Investigation of Chirp Properties Induced by Signal Amplification in Quantum-dot Semiconductor Optical Amplifiers[J].Optics Letters,2015,40(06):914-917.

[4] Gayen D K,Chattopadhyay T.Simultaneous alloptical Basic Arithmetic Operations Using QD-SOA-assisted Mach-Zehnder Interferometer[J].Journal of Computational Ele-ctronics,2016,15(03):982-992.

[5] Kotb A,Alamer F A.Dispersion on All-optical Logic XOR Gate Using Semiconductor Optical Amplifier[J].Optical and Quantum Electronics,2016,48(06):327.

[6] Zajnulina M,Lingnau B,Lüdge K.Four-Wave Mixing in Quantum-Dot Semiconductor Optical Amplifiers:A Detailed Analysis of the Nonlinear Effects[J].IEEE Journal of Selected Topics in Quantum Electronics,2017,23(06):1-12.

[7] Chen D,Wang R,Pu T,et al.A Novel Thresholder Based on XGM Effect in a DFB Laser Combined With External Optical Filtering[J].IEEE Photonics Journal,2016,8(01):1-7.

[8] Yoshida N,Fukae Y,Akahane K,et al.Temperature Dependence of Gain in a Highly Stacked Quantumdot Semiconductor Optical Amplifiier[C].Optical Components and Materials XIV. International Society for Optics and Photonics,2017:17.

[9] JI Y F,ZHANG J,ZHAO Y L,et al.All Optical Switching Networks with Energy-efficient Technologies from Components Level to Network Level[J].IEEE J. Sel.Areas Commun.,2014,32(08):1600-1614.

[10] Kotb A.Simulation of High Quality Factor All-optical Logic Gates based on Quantum-dot Semiconductor Optical Amplifier at 1Tb/s[J].Optik-International Journal for Light and Electron Optics,2016,127(01):320-325.

[11] Taleb H,Abedi K.Design of a Low-Power Alloptical NOR Gate Using Photonic Crystal Quantumdot Semiconductor Optical Amplifiers[J].Optics Letters,2014,39(21):6237-6240.

[12] 杨文华,王海龙,王兆翔等.量子点半导体光放大器的波长转换效率[J].光学学报,2017,37(04):0406005.YANG Wen-hua,WANG Hai-long,WANG Zhaoxiang,et al.Wavelength Conversion Efficiency of Quantum Dot Semiconductor Optical Amplifier[J].Acta Optica Sinica,2017,37(04):0406005.

[13] 刘松,王海龙,陈廷廷.端面反射率对单端反射半导体光放大器的影响[J].通信技术,2015,48(02):161-164.LIU Song,WANG Hai-long,CHEN Ting-ting,et al.Impact of Facet Reflectivity on Single-Port Coupled SOA[J].Communications Technology,2015,48(02):161-164.

[14] Nurmohammadi T,Abbasian K,As’adi M J,et al. Design of an Ultrafast all-optical NOR Logic Gate based on Mach-Zehnder Interfermeter Using Quantumdot SOA[J].Optik-International Journal for Light and Electron Optics,2014,125(15):4023-4029.

[15] Singh P,Tripathi D K,Jaiswal S,et al.Design and Analysis of All-optical AND,XOR and OR Gates based on SOA-MZI Configuration[J].Optics & Laser Technology,2015(66):35-44.

[16] Shi S,Wang H,Gong Q,et al.Refined Sectionalized Method of QD-SOA[J].Optik-International Journal for Light and Electron Optics,2014,125(01):504-507.