复乳液在延展流中流变行为研究

王靖涛，徐根苗，Kelkil E A，许 慎



复乳液在延展流中流变行为研究

王靖涛，徐根苗，Kelkil E A，许 慎

(天津大学化工学院，天津 300354)

为了探究复乳液内部子液滴的大小和位置分布对其流变行为的影响，采用二维波谱边界元素法数值模拟了延展流中同心复乳液和非对称复乳液的流变行为．通过改变子液滴的大小和位置得到复乳液不同的流变行为，并深入分析其变形和移动机理．研究结果表明：在不同的毛细管数下，同心复乳液内部子液滴的存在对复乳液的变形有正反双重作用；双子液滴的不对称分布导致非对称复乳液两侧界面变形和曲率不对称，界面曲率差驱使母液滴在延展流中发生移动．

边界元方法；延展流；复乳液；流变行为；界面曲率

复乳液在包裹和运输活性物质上具有独特的优势，广泛应用于医药、食品以及化妆品工业[1-6]．然而复乳液都是在通道内流体中储存和运输，并经常受到通道内几何结构限制以及外界流场的剪切作用而发生变形、破裂以及聚并等流变行为，因此对复乳液流变的实验和数值模拟研究显得很有必要[7-19]．Chen和Li等[9-10]探索了微通道结构对复乳液破裂的影响，将双层复乳液挤入并通过不同尺寸的收缩管，复乳液发生破裂并释放内部的物质．除此之外，Tanyeri等[11]专门研究了十字形微通道中的流场情况，并测绘出微通道内的无旋延展流以及水力势阱．在毫米尺度的十字形微管道装置中不同对称强度的流场下，Stegeman等[12]实验探究了简单液滴在停滞点上的变形情况．Wang和Yu等[13-14]还探究简单液滴在十字形微通道里受到非对称流场时的流变行为，研究表明发生小变形的液滴其偏移的方向只与非对称流场强度有关系．

近来，含有复杂非对称内部结构的复乳液在对称流场中定向偏移引起科学家的关注，Wang等[15-17]设计出一种多层的非对称复乳液，该种复乳液有3层，1层和2层液滴同心，第3层中有2个或3个孙液滴(grand-daughter droplet)．由于第3层中孙液滴非对称分布，导致第2层的子液滴(daughter droplet)在母液滴(mother droplet)内部发生定向偏移．Qu等[18]研究在偏心复乳液在平面拉伸流场中的流变时，发现偏心复乳液在对称流场中会向偏心子液滴一侧偏移．然而，这些流变研究工作局限于非对称复乳液移动的现象上，没有深入地分析内部非对称结构影响复乳液偏移的机理．本文借助二维波谱边界积分算法，研究了同心复乳液的内部液滴对母液滴界面变形的影响，结合毛细管数，发现子液滴的存在对母液滴的变形有正反两种作用；同时，通过发现非对称双子液滴使母液滴两侧界面在延展流中发生不对称变形，母液滴在两侧曲率差下发生移动，提出了由界面曲率差驱动复乳液在对称流场中移动的机理．

1 数值方法和物理模型

本文采用的数值方法是基于边界元的二维波谱边界积分元素法，最早是由Dimitrakopoulos等[19]共同开发并应用于微通道和简单液滴边界的离散．后来经过Wang等[17]对原有的边界积分方程进行改进，克服了原有方法只能进行简单结构液滴数值模拟的局限性，可计算和分析含有复杂内部结构的复乳液流变．采用上述具有普适性的边界积分方法计算模拟十字形通道内复乳液变形、偏移．由于十字形微通道内流体流动的雷诺数远小于1，即惯性项相对于黏性项可忽略不计，因此微通道内黏性不可压缩层流运动的控制方程可分别表示为

Stokes方程

   (1)

连续性方程

   (2)

式中：为动压力；为连续相速度；为连续相黏度；为牛顿流体的对称应力张量，其定义为

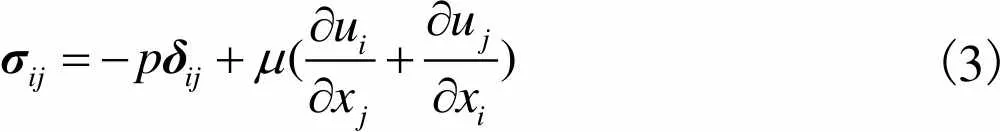
   (3)

式中为单位张量．

这里复乳液界面无限薄，界面内外两相速度相等．在复乳液的相界面S上，速度和表面应力＝·满足边界条件

   (4)

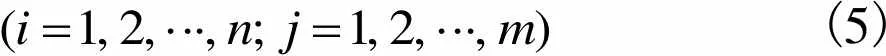
     (5)

这里微通道内壁速度边界条件设定为无滑移边界，即

   (6)

微通道进出口速度分布为抛物线，即

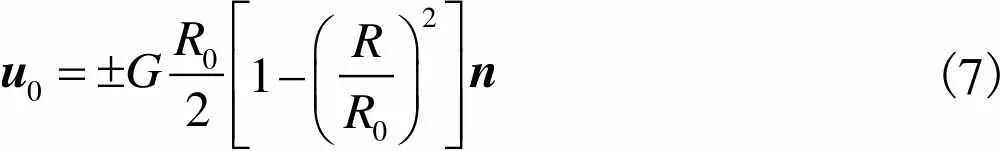
   (7)

式中：B是界面速度；0是微通道进出口速度；是单位剪切速率；“＋”表示进口速度；“-”表示出口速度．

体积流率为＝202,/3，连续相出口平均流速0,/3．

微通道和复乳液边界上离散点的速度分布可以用普适性的边界积分方程表示[13]，即

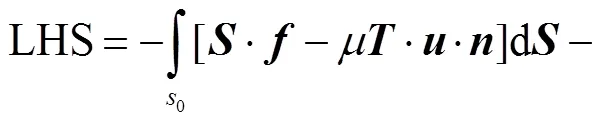
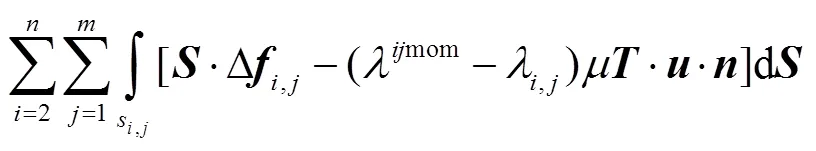
式中：第1行定义微通道边界；第2行定义复乳液最外层界面；第3行定义复乳液内部子液滴界面，其中LHS为

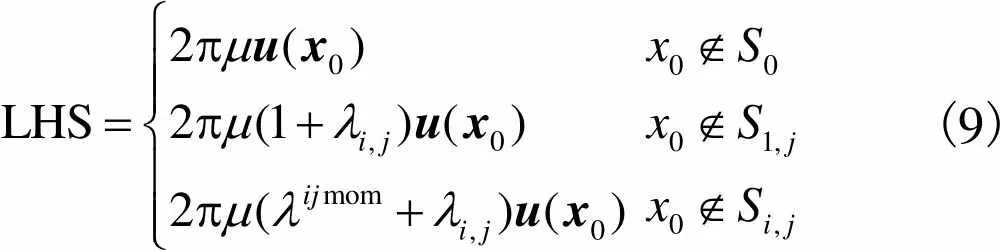
   (9)

式中、分别是控制方程的基础解系．

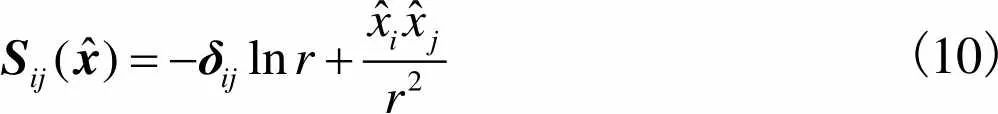
   (10)

   (11)

本文研究复乳液在十字形微通道中停滞点上受到对称延展流发生的变形和移动．图1(a)和(b)是十字形微通道和复乳液的剖面二维图，图1(c)和(d)是微通道和复乳液的立体图．为了保证计算过程判据的一致性，本文所有的变量都简化成无量纲．十字形微通道中，取微通道的管径的一半0作为长度标尺，0＝1．当流体的体积流率＝2(02,)/3时，剪切速率为单位值0，把0作为剪切速率标尺，而将0-1作为时间标尺．选取0,0为速度标尺，02,0为体积流率标尺．0为连续相的黏度标尺，0,0,0为表面张力的标尺，0,0为压力标尺．在本文所进行的模拟计算中，假定连续相中进口的平均速度＝1，连续相的黏度＝1，黏度比＝1.2均不变．流动参数毛细管数定义为：Ca＝/，可通过改变乳液界面的表面张力来改变毛细管数．描述液滴变形系数定 义[20]为

   (12)

复乳液最外层液滴的半径是MD＝0.50，内部左侧液滴和右侧液滴的半径分别为L和R，内部左侧液滴与最外层液滴中心点的距离为偏心距L，同理内部右侧液滴的偏心距为R．另外为了文章叙述简洁，本文定义：复乳液最外层液滴为母液滴，内部液滴为子液滴．母液滴质心移动距离为，子液滴的总体积分率为，最初液滴形状均为球形．其中子液滴体积分率定义为

   (13)

2 数值结果

本文采用的数值方法能够准确地模拟复乳液的流变行为，其有效性在以前的研究工作中得到很好的证明[7, 13-17]．

2.1 十字形微通道中简单液滴和同心复乳液的变形

图2中为同心复乳液(concentric multiple-emulsion globules)的结构及其流变示意，第1层为母液滴，第2层为子液滴，其中母液滴的半径为MD，子液滴的半径为DD，子液滴的体积分率为＝DD2/MD2．液滴外部是完全对称的延展流，同心复乳液在停滞点上只会发生对称变形．Chen等[21]在研究简单剪切流中同心复乳液的变形发现，内核子液滴的存在对母液滴的变形有促进或抑制作用．在对称延展流中，本文同样发现子液滴的存在对母液滴的变形存在正反双重影响．

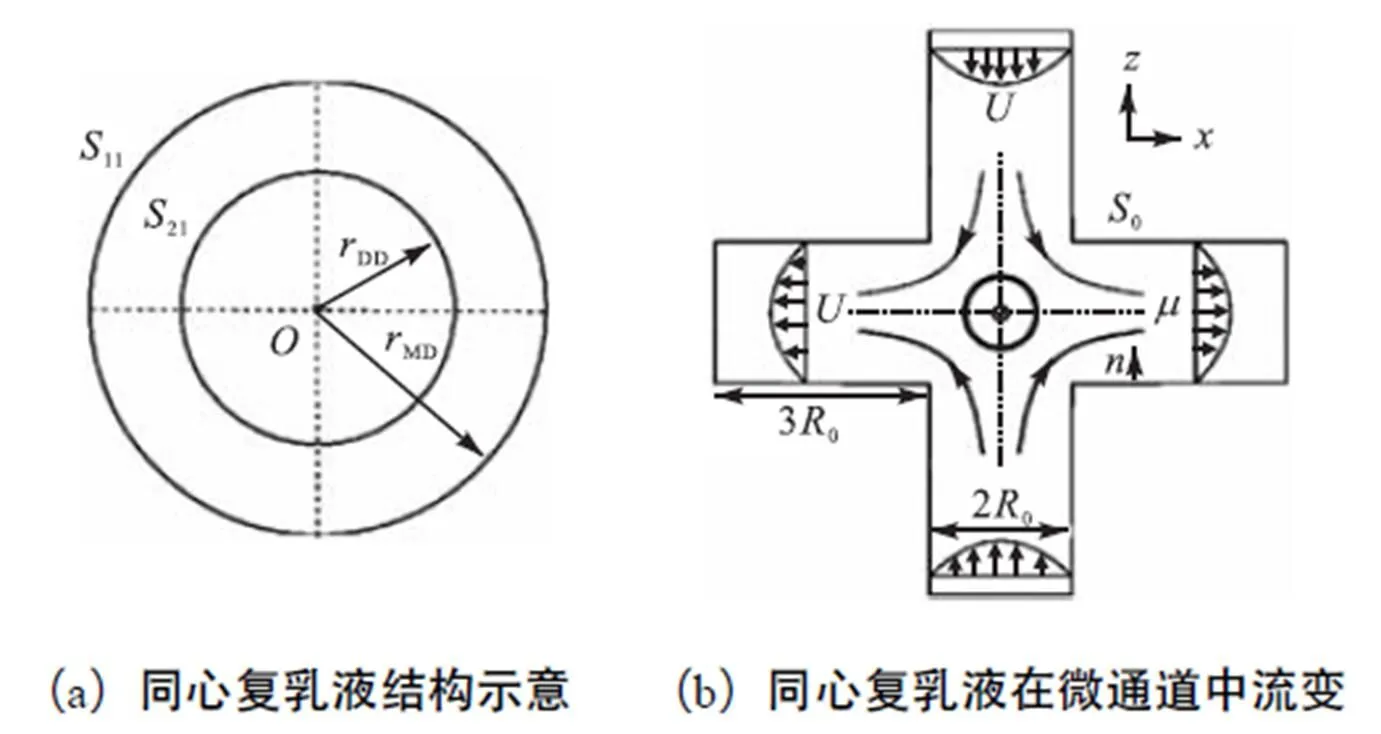
图2 同心复乳液结构及其流变示意

为了研究子液滴对母液滴变形的影响，本文对比了相同毛细管数下简单液滴和同心复乳液在同一时刻下的变形．在较小毛细管数下，同心复乳液比简单液滴变形要大，子液滴的存在促进了母液滴的变形(见图3(a))；然而在较大的毛细管数下，同心乳液变形比简单液滴要小，同心复乳液内子液滴的存在对界面变形起了抑制作用(见图3(b))．也就是说在母液滴小变形时，子液滴对母液滴界面变形起促进作用；在母液滴大变形时，子液滴对母液滴变形起抑制作用.

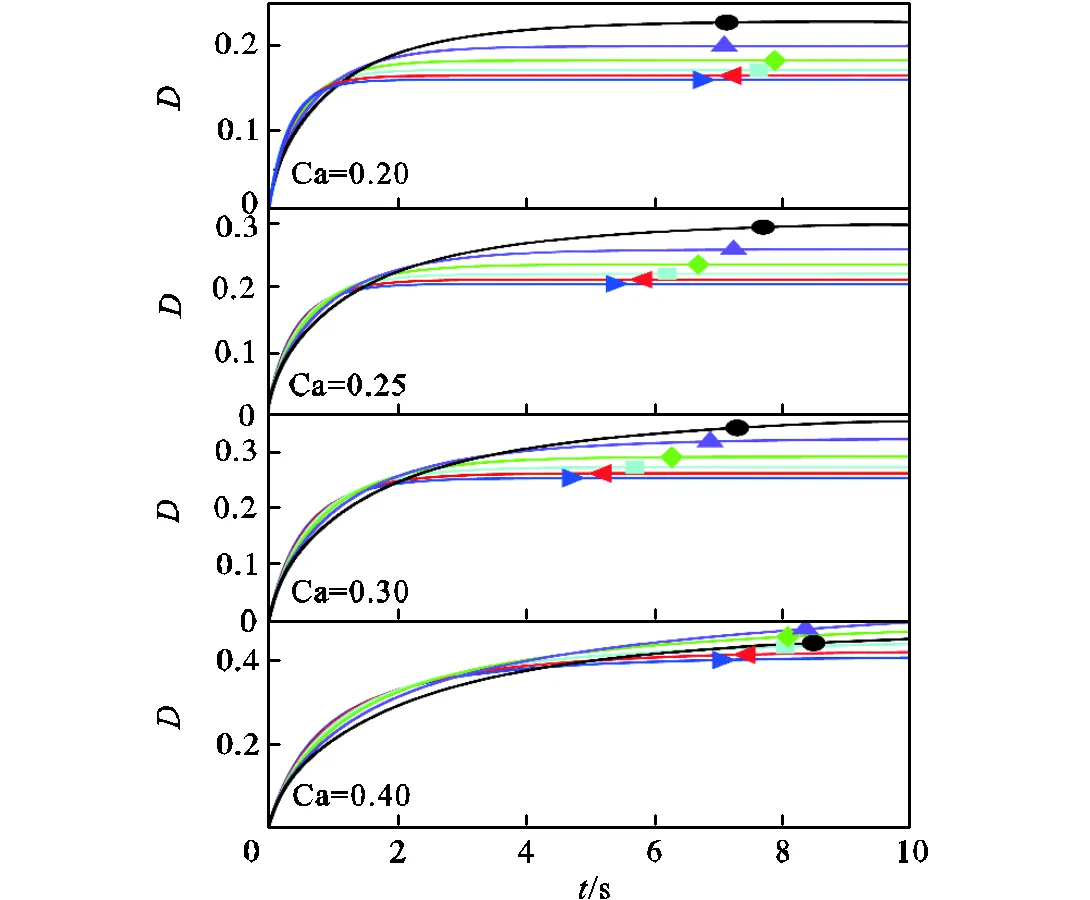
如图4所示，本文探究了子液滴体积以及毛细管数对母液滴变形的影响．毛细管数Ca＝0.20时，母液滴的最终变形是随着子液滴体积增大而增大，即子液滴体积对母液滴稳定形变有重要影响．同时，毛细管数的增大，也促进同心复乳液最终稳定变形增大．总的来说，在液滴不发生分断的小变形下，含有小体积子液滴的母液滴在较小的毛细管数下最终变形较小，含有大体积子液滴的母液滴在较大的毛细管数下最终变形较大．

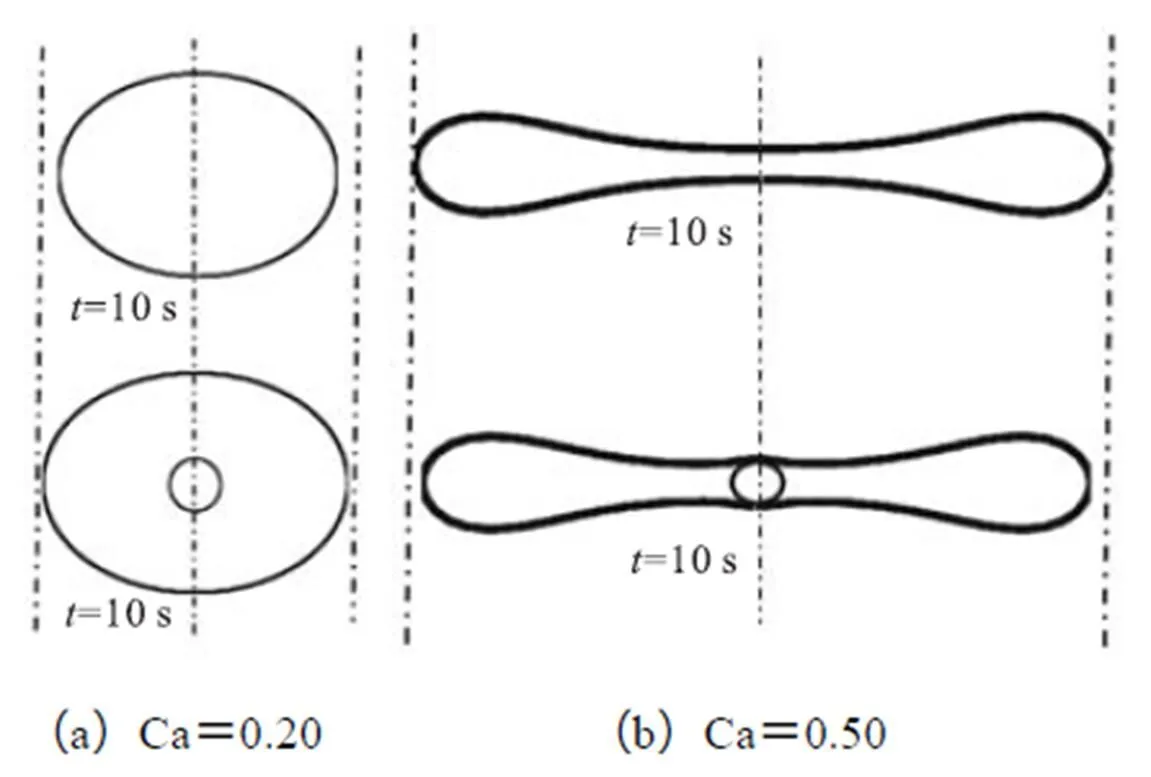
图3 简单液滴和同心复乳液在不同毛细管数下的形变(F＝4%)

本文从液滴内部的流场(旋涡)来解释上述现象，液滴内部形成的4个漩涡对液滴变形起关键作用，均匀性越好的漩涡在抵抗变形能力方面表现越强[21].本文根据母液滴界面变形的规律，可将内部流场演变过程分成3个阶段：环流形成期、环流变形期和环流稳定期．图5所示为不同时刻下，液滴内部流场的分布．环流形成期中，子液滴的抑制作用使同心复乳液在该阶段的变形小于简单液滴．内部环流在环流变形期中形成，同心复乳液界面变形比简单液滴大.因为子液滴的存在减弱内部4个环流的对称性，对称性差的环流抵抗外部变形能力较低，容易被压得更扁．环流稳定期中，环流被压扁到一定程度并保持稳定，此时外部的剪切和内部的抵抗达到平衡，母液滴总的变形系数稳定．子液滴体积越大，母液滴内部形成的环流对称性越差，导致母液滴最后变形越大．

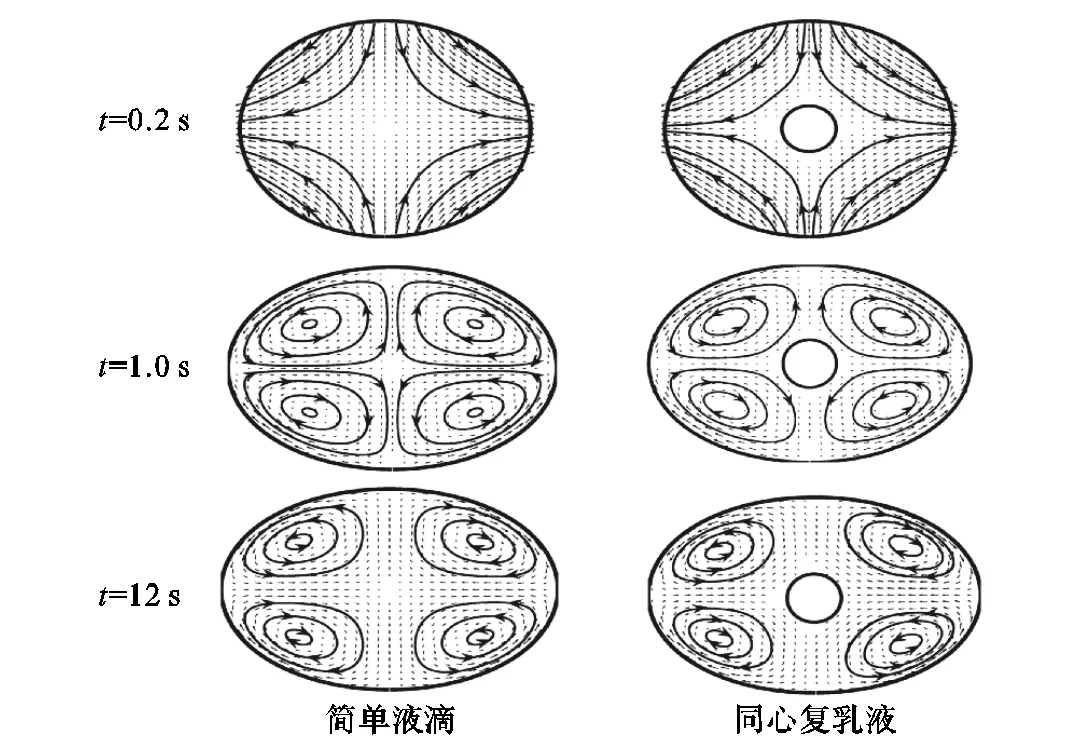
图5 在相同毛细管数下，简单液滴和同心复乳液内部流场随时间的演变

2.2 十字形微通道中非对称复乳液的偏移

含有两个不对称子液滴的复乳液在十字形微通道中发生移动，这种流变行为跟母液滴内部非对称子液滴有关．图6描述的是双层复乳液在十字孔型微通道中稳定变形、移动时流场和压力场．为了更好地研究非对称复乳液的流变行为，本文对比了一组完全对称的复乳液(见图6(a))．影响复乳液母液滴行为的流场可以分成两部分：外部延展流，母液滴和子液滴界面之间的流场．对称复乳液由于外部延展流的剪切，母液滴发生小变形并在内部形成4个对称的环流，子液滴也在内部流场的作用下发生变形并都向中间靠近．由于外部流场和液滴内部结构的完全对称，因此内部流场和压力场分布均匀且左右对称，此时复乳液只发生变形至变形稳定，不发生偏移(见图6(a))．非对称复乳液由于外部的剪切作用也会在内部逐渐形成4个环流，同时左侧上下两个环流彼此相离，右侧上下两个环流彼此靠近．因为子液滴位置不对称，内部流场和压力逐渐分布不均匀，内部4个稳定环流在压力差下被破坏，流场向右侧发生定向移动(内部流线走向见图6(b)、(c))．同时母液滴由于内部压力驱动也开始向右侧移动．

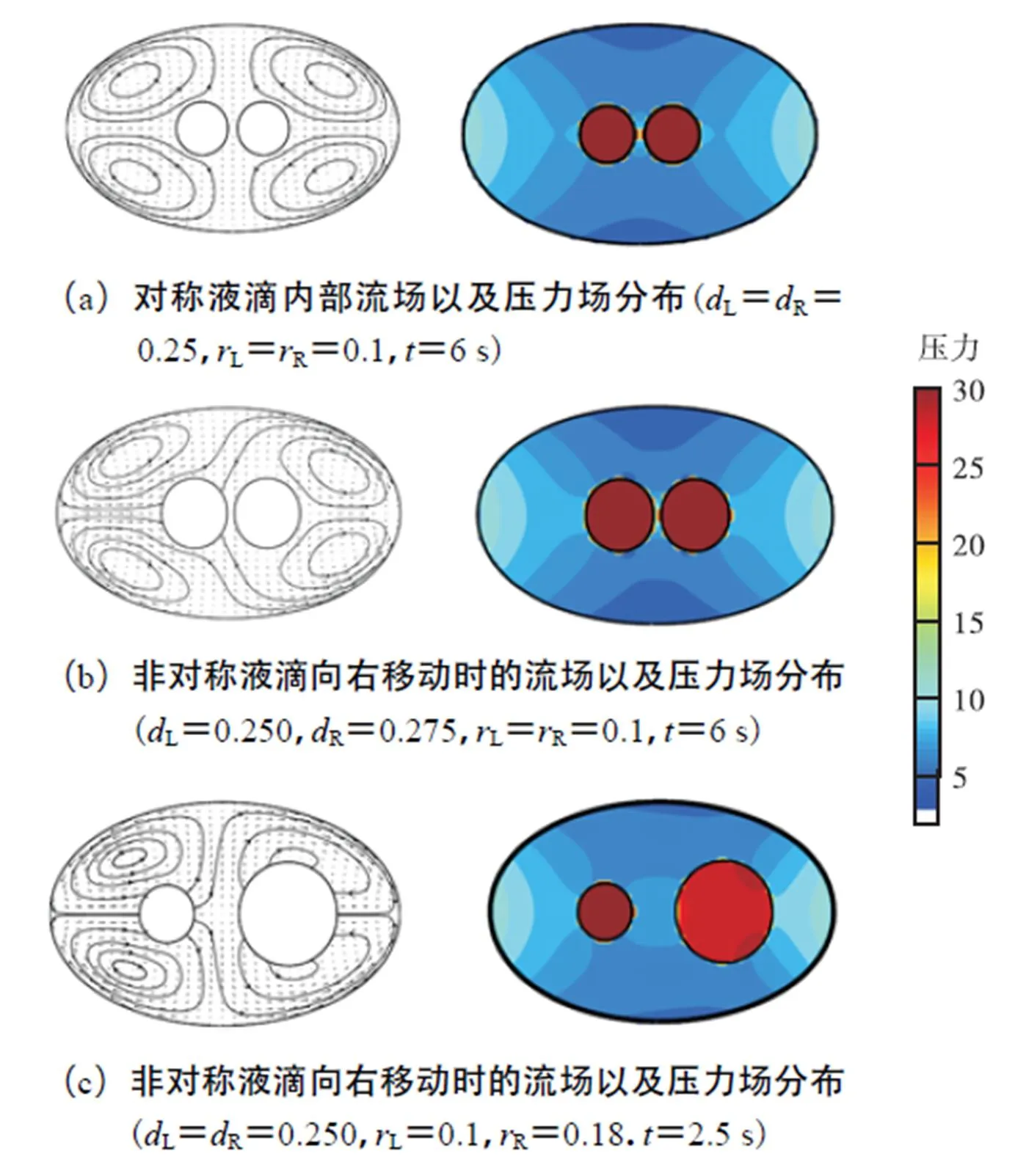
图6 液滴内部流场以及压力场分布

为了系统研究子液滴偏心距离和体积对母液滴移动的影响，这里系统地研究了非对称结构对其移动的影响．图7所示为在子液滴不同偏心距或不同体积的非对称内部结构下，母液滴的质心位移距离随时间的变化曲线．图7(a)中每组复乳液的子液滴初始半径都相等，左侧子液滴的初始偏心距为定值，L＝R＝0.10，L＝0.250，右侧子液滴初始偏心距分别是0.250、0.275、0.300、0.325、0.350、0.370．图7(b)中每组非对称复乳液的子液滴偏心距都相等，L＝R＝0.250，左侧子液滴初始的体积为定值，右侧子液滴初始体积逐渐增大，即L＝0.10，R分别是0.10、0.14、0.16、0.18、0.22、0.24．这种非对称结构下，复乳液在对称延展流中发生移动的方向都是向右移动．子液滴位置或体积上不对称性不仅造成母液滴的偏移，而且影响其移动的速度．子液滴偏心距越大或者体积越大造成母液滴在停滞点上更早地发生移动，并且速度越来越快．由此可知，相同的毛细管数情况下，非对称性强的结构更易促进母液滴的移动．

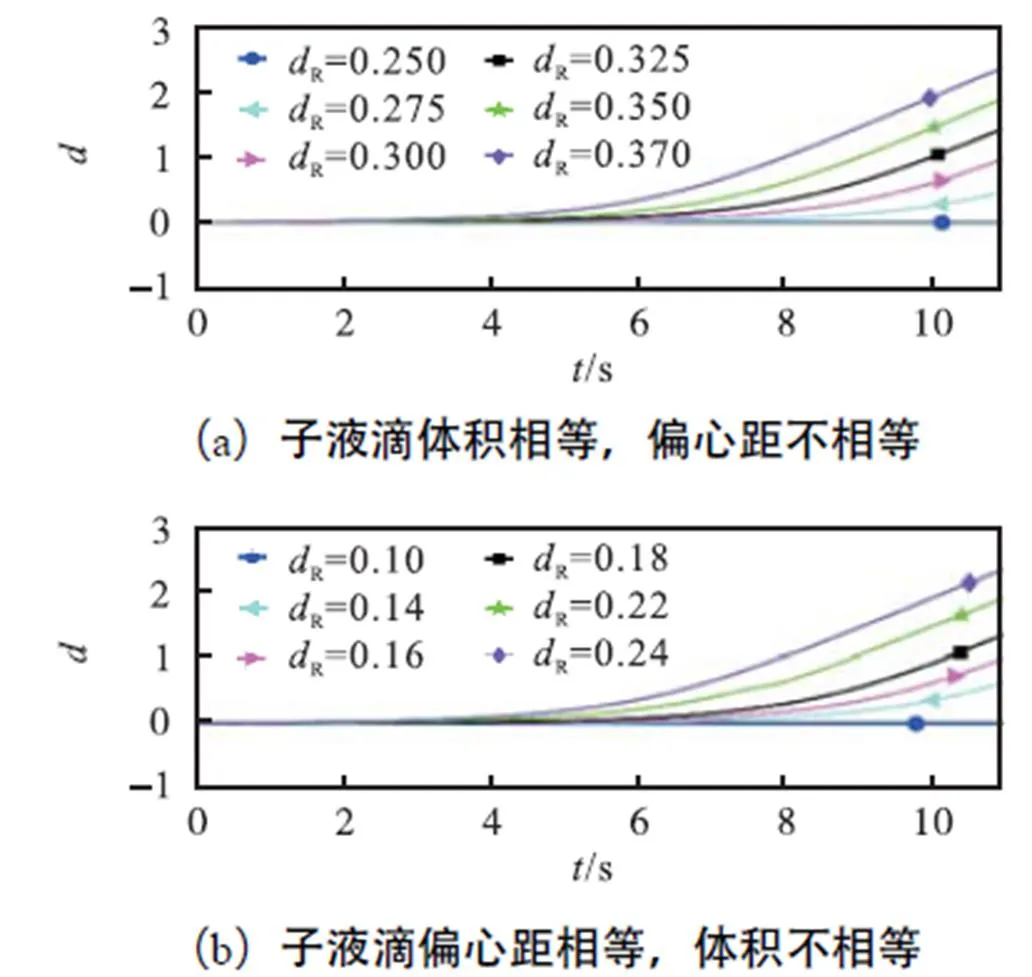
图7 非对称复乳液的质心位移随时间的变化(Ca＝0.26，l＝1.2)

为了研究母液滴偏移的机理，本文探究图8和图9中非对称复乳液其两侧端点上的曲率和压力值随时间的变化．其中1和2分别代表母液滴左侧和右侧端点曲率，1和2分别代表母液滴左侧和右侧端点附近的压力值．子液滴的存在对母液滴变形有支撑和促进作用，当两侧子液滴完全对称分布在母液滴的内部，母液滴两侧变形程度相同．然而，当两个子液滴的位置或体积上不对称，子液滴对母液滴两侧变形的贡献值不同，母液滴两侧曲率不相同．如图8(a)和(b)曲率放大图所示，当右侧子液滴距离更远、体积更大，其对母液滴右侧界面起支撑作用越强，抑制其右侧变形．所以，左侧的曲率的绝对值大于右侧，其界面曲率差异造成的压力也是左侧大于右侧(图9(a)和(b)压力放大图)．由于子液滴的不对称性，造成母液滴两侧曲率变化不同，母液滴在内部压力和流场的不对称下向右移动．母液滴向右偏移后，外部延展流对母液滴界面向右的拖曳力大于向左的拖曳力，而这种外部流场的不对称反过来又促进母液滴向右移动[13-14]，同时母液滴的左侧曲率绝对值由于内外流场的作用变大，而右侧曲率减小．总的来说，内部子液滴不对称性越强，液滴变形过程中界面上表现出左右两侧曲率差异越大，母液滴偏移速度越快．

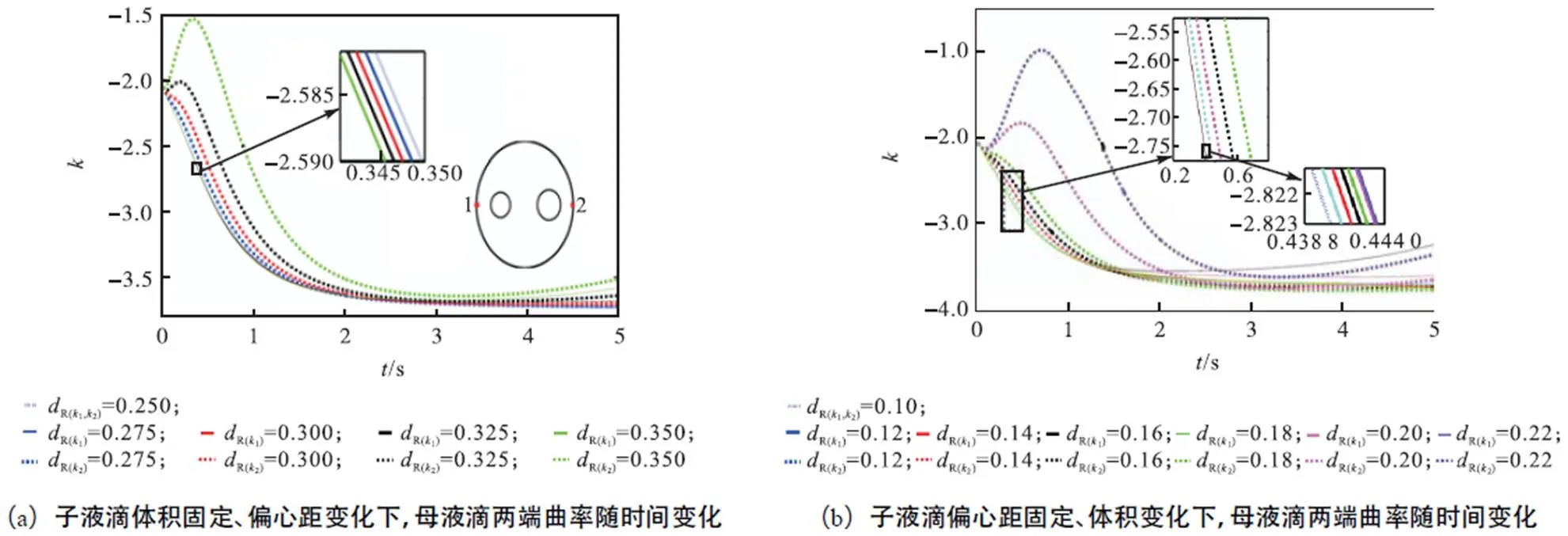
图8 非对称复乳液两侧端点上的曲率随时间的变化(Ca＝0.26，l＝1.2)

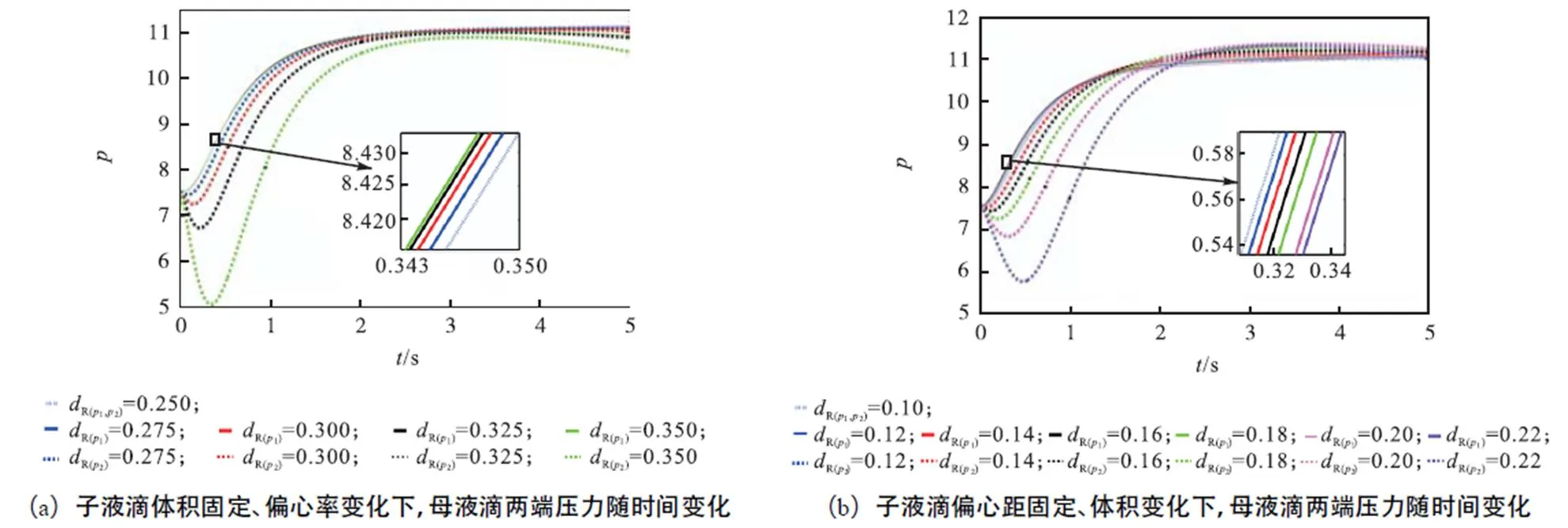
图9 非对称复乳液两侧端点上的压力随时间的变化(Ca＝0.26，l＝1.2)

3 结 语

本文采用普适性的特殊边界元方法，数值模拟了简单液滴和非对称复乳液在十字形微通道中流变．复乳液内部子液滴的存在对母液滴在延展流下的变形有正反影响：①在母液滴大变形下，表现为抑制作用；②母液滴小变形下，表现为促进作用．同时，含有非对称双子液滴的复乳液由于其内部结构非对称性，复乳液在对称延展流中发生定向偏移．这是因为子液滴非对称分布造成母液滴界面曲率上的差异，从而使复乳液在内部压力的驱动下发生偏移．这一成果可能启迪实现软颗粒在界面曲率差驱动下的运动，从而为研究和设计具有合适内部结构的复乳液用于活性物质可控释放等流变行为提供理论基础．

［1］ Oh J K，Drumright R，Siegwart D J，et al. The development of microgels/nanogels for drug delivery applications[J].，2008，33(4)：448-477.

［2］ Shah R K，Shum H C，Rowat A C，et al. Designer emulsions using microfluidics[J].，2008，11(4)：18-27.

［3］ Nie Z，Li W，Seo M，et al. Janus and ternary particles generated by microfluidic synthesis：Design，synthesis，and self-assembly[J].，2006，128(29)：9408-9413.

［4］ Yen B K H，Stott N E，Jensen K F，et al. A continuous-flow microcapillary reactor for the preparation of a size series of cdse nanocrystals[J].，2003，15(15)：1858-1862.

［5］ Wiles C，Watts P. ChemInform abstract：Recent advances in micro reaction technology[J].，2011，47(23)：6512-6535.

［6］ Mcclements D J. Advances in fabrication of emulsions with enhanced functionality using structural design principles[J].，2012，17(5)：235-245.

［7］ 王靖涛，韩俊杰，陶 君，等. 利用波谱边界元素法研究微通道内液滴、气泡的变形和聚并[J]. 化工进展，2011(增2)：26-29.

Wang Jingtao，Han Junjie，Tao Jun，et al. Study on deformation and aggregation of droplets and bubbles in microchannels using spectral boundary element method[J].，2011(S2)：26-29(in Chinese).

［8］ 马友光，付涛涛，朱存英. 微通道内气液两相流行为研究进展[J]. 化工进展，2007，26(8)：1068-1074.

Ma Youguang，Fu Taotao，Zhu Cunying. Study on the behavior of gas-liquid two-phase flow in microchannels[J].，2007，26(8)：1068-1074(in Chinese).

［9］ Chen H，Li J，Shum H C，et al. Breakup of double emulsions in constrictions[J].，2011，7(6)：2345-2347.

［10］ Li J，Chen H，Stone H A. Breakup of double emulsion droplets in a tapered nozzle[J].，2011，27(8)：4324-4327.

［11］ Tanyeri M，Johnson-Chavarria E M，Schroeder C M. Hydrodynamic trap for single particles and cells[J].，2010，96(22)：224101.

［12］ Stegeman Y W，Chesters A K，Fn V V D，et al. Breakup of (non-)newtonian droplets in a time-dependent elongational flow[C]//. Hertogenbosch，The Netherlands，1999：1-15.

［13］ Wang J T，Yu D M. Asymmetry of flow fields and asymmetric breakup of a droplet[J].，2015，18(4)：709-715.

［14］ Yu D M，Zheng M M，Wang J T，et al. Asymmetric breakup of a droplet in an axisymmetric extensional flow [J].2016，24(1)：63-70.

［15］ Wang J T，Wang X Y，Tai M，et al. Oriented shift and inverse of the daughter droplet due to the asymmetry of grand-daughter droplets of multiple emulsions in a symmetric flow field[J].，2016，108(2)：021603.

［16］ Wang J T，Liu J X，Han J J，et al. Rheology investigation of the globule of multiple emulsions with complex internal structures through a boundary element method[J].，2013，96(96)：87-97.

［17］ Wang J T，Liu J X，Han J J，et al. Effects of complex internal structures on rheology of multiple emulsions particles in 2D from a boundary integral method[J].，2013，110(6)：066001.

［18］ Qu X，Wang Y. Dynamics of concentric and eccentric compound droplets suspended in extensional flows[J].，2012，24(12)：2753-2765.

［19］ Dimitrakopoulos P，Wang J. A spectral boundary element algorithm for interfacial dynamics in two-dimensional Stokes flow based on Hermitian interfacial smoothing[J].，2007，31(7)：646-656.

［20］ Taylor G I. The viscosity of a fluid containing small drops of another fluid[J].，1932，138(834)：41-48.

［21］ Chen Y P，Liu X D，Zhang C B，et al. Enhancing and suppressing effects of an inner droplet on deformation of a double emulsion droplet under shear[J].，2015，15(5)：1255-1261.

(责任编辑：田 军)

Rheological Behaviors Investigation of Multiple-Emulsion Globules in Extensional Flows

Wang Jingtao，Xu Genmiao，Kelkil E A，Xu Shen

(School of Chemical Engineering and Technology，Tianjin University，Tianjin 300354，China)

In order to explore the impact of inner droplets’ size and position on rheological behaviors of outer droplets，the two-dimensional spectral boundary element method was employed to simulate the rheological behaviors of concentric multiple-emulsion globules and asymmetric multiple-emulsion globules in extensional flows. The different rheological behaviors of multiple-emulsion globules were obtained by changing the size and position of the inner droplets，and the mechanism of deformation and movement was deeply analyzed. The results show that the inner droplet of the concentric multiple-emulsion globules has positive or negative effects on the deformation of the globules under different capillary numbers. The asymmetric layout of the double-emulsion droplets leads to the asymmetric deformation of the globules with different interface curvatures，which causes the oriented shift of the globules.

boundary element method；extensional flows；multiple-emulsion globules；rheological behaviors；interface curvature

10.11784/tdxbz201703098

TQ021.4

A

0493-2137(2018)01-0027-07

2017-03-29；

2017-05-05.

王靖涛（1973—  ），男，博士，教授.

王靖涛，wjingtao928@tju.edu.cn.

2017-05-17.

http://kns.cnki.net/kcms/detail/12.1127.N.20170517.1128.006.html.

国家自然科学基金资助项目(21376162，21576185)．

the National Natural Science Foundation of China(No.,21376162 and No.,21576185).