永磁球形电动机空芯定子线圈磁场的解析分析

李洪凤，李天梦，韩 冰



永磁球形电动机空芯定子线圈磁场的解析分析

李洪凤1，李天梦1，韩 冰2

(1. 天津大学电气自动化与信息工程学院，天津 300072；2. 国网天津市电力公司检修公司，天津 300230)

永磁球形电机定子线圈呈空芯圆柱形结构，由多匝导线缠绕在柱状铝芯上，离散分布在定子球壳内壁不同经、纬度线交叉点处．针对采用集中绕制方式的定子线圈的结构特点，基于毕奥-萨伐尔定律，并考虑球形电机定子线圈在定子坐标系中的位置关系对问题分析复杂性的影响，首先推导得到了任意位置单匝线圈在空间任意点处的磁场分布，并与现有文献进行了比较验证．其次将单匝线圈推广到多层多匝线圈，求解得到了任意位置多层多匝定子线圈在空间任意点处的磁场分布解析表达式．最后就定子线圈在不同路径上的磁场分布情况，与有限元法所得结果进行了比较，证明了该解析表达式的有效性．

永磁球形电机；毕奥-萨伐尔定律；定子线圈磁场分布；有限元法

涡流损耗是永磁球形电机(permanent magnet spherical motor，PMSM)设计的关键性问题，而定子线圈磁场是引起电机涡流损耗的主要原因，因此，准确计算永磁球形电机内涡流损耗的前提是对定子线圈磁场进行分析研究．

定子线圈磁场较为复杂，有关电机定子线圈磁场的研究多是借助于有限元法进行仿真分析[1-4]，并基于有限元法的分析结果对定子线圈做进一步的优化改进[5-8]．与有限元法相比，解析法不仅能够准确反映电机参数对磁场分布的影响，而且能够提高求解计算速度[9-15]．文献[14-15]借助于矢量磁位对普通电机定子线圈磁场进行了分析计算，将定子线圈等效为位于线圈间隙的厚度无穷小的电流片，通过逐步简化求解得到了定子线圈磁场分布解析表达式．永磁球形电机定子线圈磁场分析需要求解的是集中绕组三维场问题，边界条件复杂，很难将其简化为二维模型进行分析求解．文献[16]采用磁场积分法得到了永磁步进球形电机定子线圈在空间场点磁场分布的计算公式，但未求解得到最终的解析表达式．文献[17-19]采用不同的方法对永磁球形电机定子线圈磁场进行了求解，其中，文献[18]采用的方法难以对电机结构进行准确刻画，通常只适合于气隙处磁通密度的估计，文献[19]中的等效定子线圈与实际定子线圈存在一定的偏差，将会影响所得解析表达式的准确性．

毕奥-萨伐尔定律是电磁学最基本的定律，它可以计算任意稳恒传导电流在空间产生的磁感应强度，文献[20-21]采用该定律求解得到了圆电流在空间任意位置处的磁场分布，并利用软件仿真或实验测试方法验证了该方法的准确性．本文针对永磁球形电机柱形定子线圈的结构特点，基于毕奥-萨伐尔定律求解了任意位置单匝、多层多匝定子线圈在空间任意点的磁场分布，并与有限元结果进行了对比，验证了本文解析方法的有效性．

1 永磁球形电机的基本结构

永磁球形电机的实物模型如图1(a)所示，电机由球形转子和球壳型定子构成，6块永磁体按N、S极交替贴于转子赤道一周．永磁体采用钕铁硼，定子线圈采用铜线．定子线圈采用集中绕制方式，由多匝导线缠绕在柱状铝芯上，沿定子内壁赤道处、北纬22.5°线处、南纬22.5°线处放置3层，每层18个线圈，均匀分布在定子球壳内壁不同经纬度交叉点处．永磁球形电机的原理如图1(b)所示，按照一定的通电规律，当给赤道处的定子线圈通电时，可以实现球形电机的自转运动，当同时给不同纬度线上的定子线圈通电时，可以实现球形电机的俯仰和偏航运动．定子线圈在空间任意点处产生的磁场分为3个磁通密度分量：径向磁通密度分量B、纬向磁通密度分量B、周向磁通密度分量，3个磁通密度分量的单位矢量分别为、、，其方向如图1(b)所示．

图1 永磁球形电机的实物模型与原理

2 基于毕奥-萨伐尔定律求解定子线圈磁场

2.1 永磁球形电机定子线圈在定子坐标系中的位置

永磁球形电机定子线圈在空间任意点产生的磁场是所有不同位置定子线圈在以转子球心为原点的定子坐标系下磁场分布的叠加．求解出任意位置单个定子线圈在空间任意点的磁场分布，进而运用叠加原理可得电机定子线圈在空间任意点的磁场分布．

图2为永磁球形电机某位置第个柱形定子线圈的位置示意．其中，图2(a)为该定子线圈在以转子球心为坐标原点的定子坐标系下的示意，图2(b)为该定子线圈在以定子线圈中心点为坐标原点，以定子线圈中心轴线为轴的定子线圈坐标系下的示意．

图2 任意位置定子线圈示意

其中，表示定子线圈中心点到转子球心的距离；、分别表示第个定子线圈中心轴线与轴正向和轴正向之间的夹角；1、2分别表示定子线圈的内外半径；为定子线圈的有效长度；为空间任一点，记为场点；为线圈上任一点，记为源点；dd为源点处的电流元．

首先建立定子坐标系与定子线圈坐标系间的映射关系．取空间任一点，记该点在定子坐标系中的坐标为(1，1，1)，在定子线圈坐标系中的坐标为(1，1，1)．将定子坐标系平移至其坐标原点与定子线圈中心点重合的位置，将该点在平移后的坐标系中的坐标记为(3，3，3)，则(1，1，1)与(3，3，3)满足关系

   (1)

   (2)

   (3)

将上述平移得到的坐标系绕轴逆时针旋转，记该点在此时旋转后的坐标系中的坐标为(4，4，4)，满足关系

   (4)

   (5)

   (6)

将式(1)～式(3)分别代入式(4)～式(6)中可得

     (7)

     (8)

   (9)

继续绕轴逆时针旋转θ，此时该坐标系将与定子线圈坐标系重合，满足关系

   (10)

   (11)

   (12)

将式(7)～式(9)分别代入式(10)～式(12)中可得

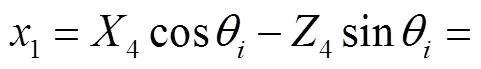
     (13)

   (14)

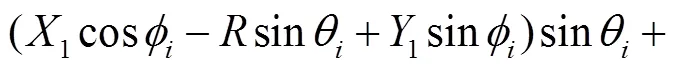
    (15)

最终整理得到空间任一点在定子坐标系和定子线圈坐标系间的坐标转换关系为

   (16)

   (17)

     (18)

将B、B、B定义为定子坐标系中的磁通密度分量，B、B、B定义为定子线圈坐标系中的磁通密度分量，则满足关系

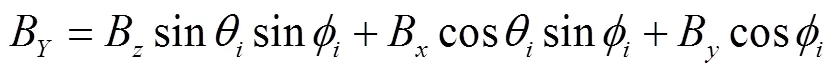
   (21)

2.2 基于毕奥-萨伐尔定律求解单匝线圈的磁场

当图2(b)所示定子线圈为单匝时，即为图3所示的单匝线圈示意．

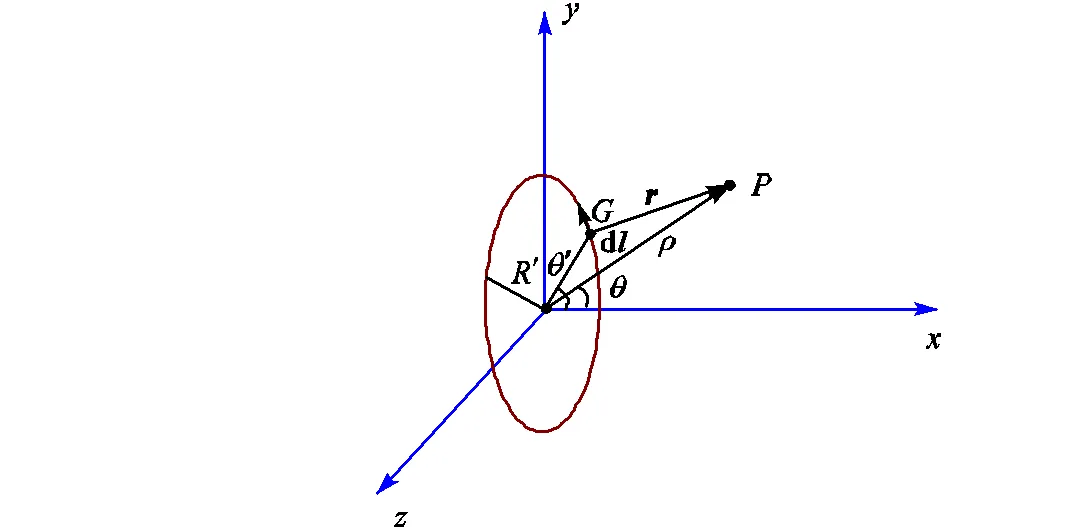
图3 单匝线圈示意

设单匝线圈的电流大小为；记源点在定子线圈坐标系中的坐标为(，，0)(直角坐标系下)，或(，，0)(柱坐标系下)；空间任一场点在定子线圈坐标系中的坐标为(，，)(直角坐标系下)，或(，，)(柱坐标系下)．源点处的电流元d在场点处的磁场可由毕奥-萨伐尔定律确定．

由毕奥-萨伐尔定律可知，源点处的电流元d在场点处的磁感应强度为

   (22)

式中：为真空磁导率；为由源点向场点所引的矢径；为矢径的模值；d为单匝线圈的长度微分，方向为源点的切线方向，正负号取决于线圈线电流密度的方向，文中规定从轴正向望去，逆时针为正，顺时针为负．

     (23)

式中′为单匝线圈的半径．

矢径为

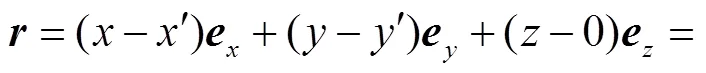
     (24)

矢径的模长为

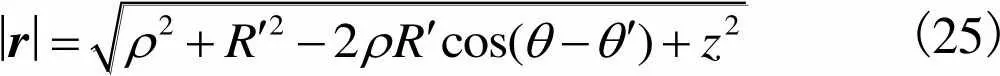
   (25)

将式(23)～式(25)代入式(22)得

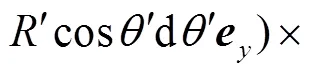
     (26)

整理得d的3个分量分别为

     (27)

     (28)

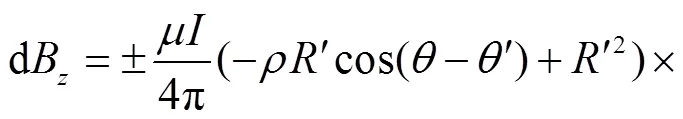
    (29)

     (30)

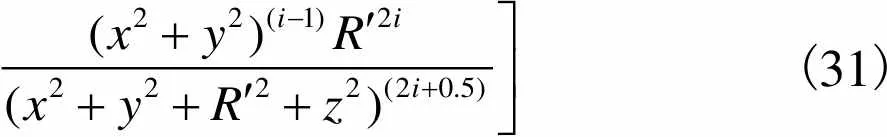
     (31)

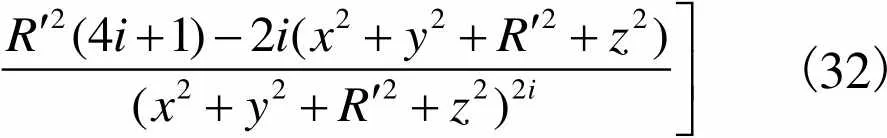
     (32)

式(16)～式(21)给出了空间任一点以及磁通密度各分量在定子坐标系和定子线圈坐标系之间的转换关系，运用该关系式，可得单匝定子线圈在以转子球心为原点的定子坐标系的空间任一点产生的磁场分布解析表达式．

运用该求解思路可降低直接从定子坐标系入手分析定子线圈磁场的复杂度，使得求解大大简化，且不需要讨论奇异点的特殊情况．

2.3 基于毕奥-萨伐尔定律求解多层多匝线圈磁场

对于图2(b)所示的定子线圈为多层多匝时，记源点在定子坐标系中的坐标为(，，)(直角坐标系下)或(，，)(柱坐标系下)；场点和单匝线圈时定义一致．此时源点处的电流元dd在场点处的磁感应强度为

   (33)

式中d表示d面内所流过的电流大小．

   (34)

   (35)

将式(34)和式(35)代入式(33)，整理得源点处的电流元dd在场点处的磁感应强度为

   (36)

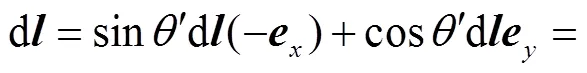
     (37)

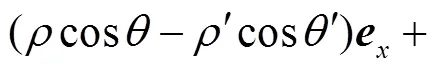
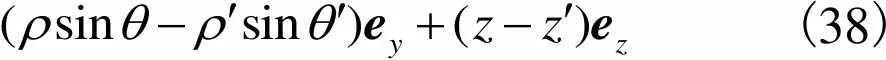
     (38)

矢径的模长为

     (39)

将式(37)～式(39)分别代入式(36)，整理得

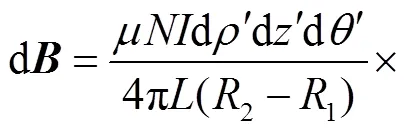
     (40)

整理得d的3个分量分别为

     (41)

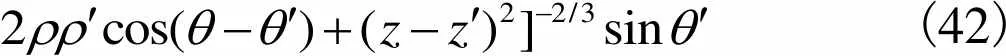
(42)

     (43)

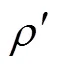
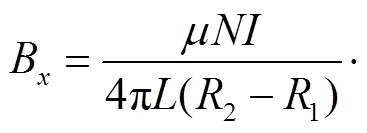
     (44)

     (45)

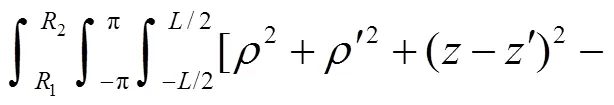
     (46)

经积分运算整理得

(47)

   (48)

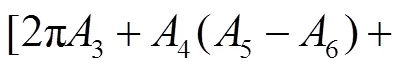
     (49)

   (50)

   (51)

   (52)

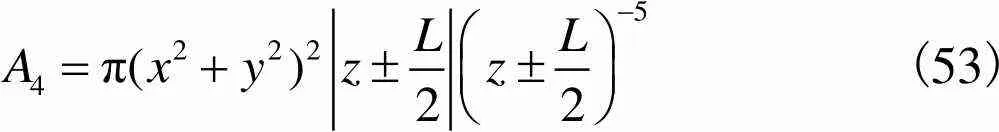
   (53)

     (54)

     (55)

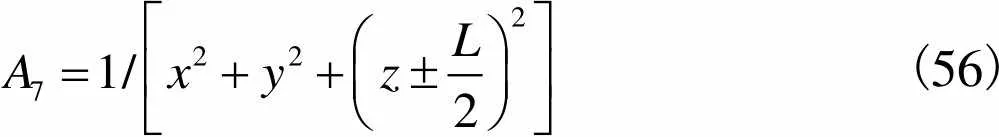
   (56)

   (58)

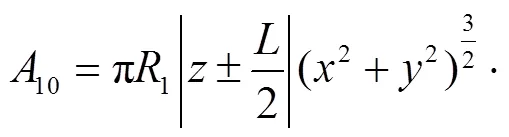
     (59)

     (60)

     (61)

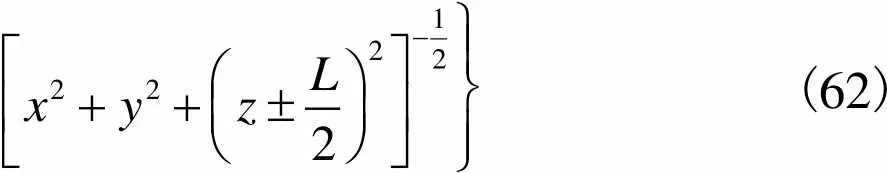
     (62)

     (63)

式(16)～式(21)给出了空间任一点以及磁通密度各分量在定子坐标系和定子线圈坐标系之间的转换关系，运用该关系式，最终可得任意位置多层多匝定子线圈在以转子球心为原点的定子坐标系的空间任一点产生的磁场分布解析表达式．

3 有限元仿真验证

为验证多层多匝定子线圈磁场分布解析方法的正确性，选取定子线圈中心轴线与轴重合，即θ＝90°，＝0°的定子线圈为研究对象，就3个不同路径的磁场分布情况与有限元所得结果进行对比．相关参数如表1所示，空载转速为300,r/min．

表1 结构和材料参数

Tab.1 Structure and material parameters

图4所示为部分电机参数示意，电机气隙长度指的是永磁体外径ro与定子内径si之间的距离．

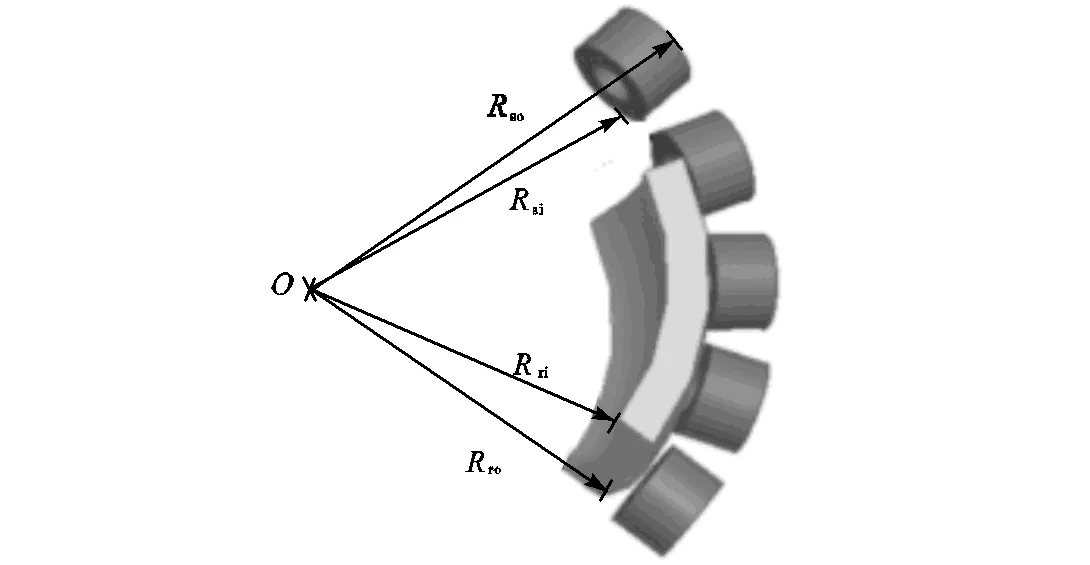
图4 永磁球形电机部分参数示意

图5所示为采用ANSOFT有限元分析软件Maxwell 3D根据表1中的电机参数建立的永磁球形电机有限元模型及其剖分结果，采用自适应网格剖分方式进行剖分．求解场域内的永磁体、气隙、线圈与铁芯之间的边界满足自然边界条件，区域最外层边界满足第一类齐次边界条件．

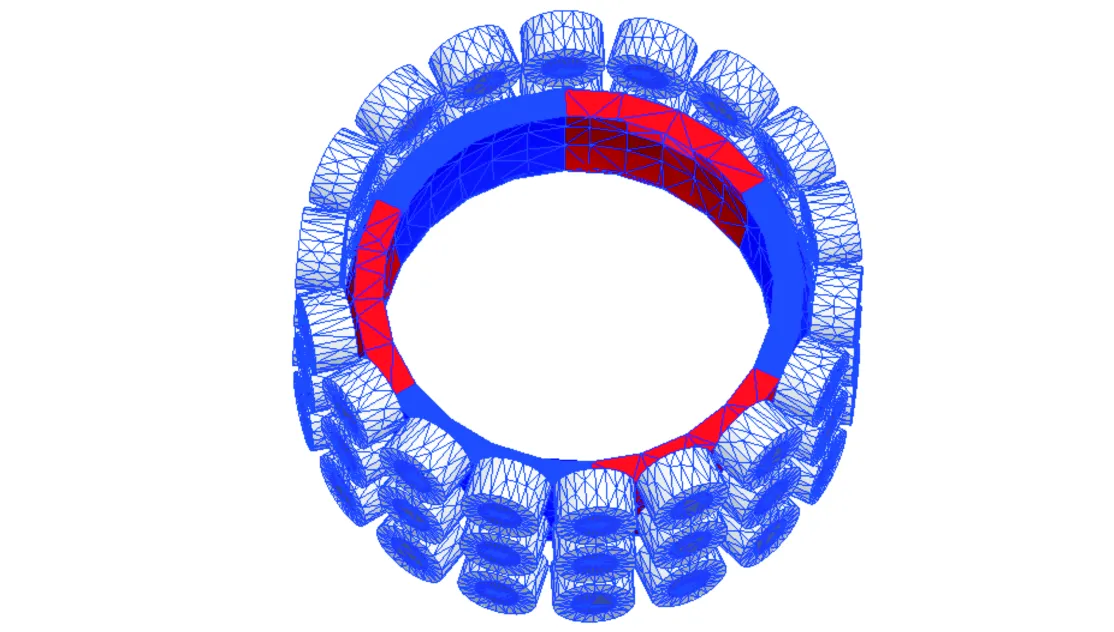
图5 永磁球形电机有限元模型及其剖分结果

图6给出了场点路径选取在定子线圈的中心轴线上时，解析法和有限元法所得磁通密度各分量对比.

从图6中可以看出，解析法所得定子线圈中心轴线上的磁场分布与有限元结果几乎吻合．由于线圈中心轴线与轴重合，当场点选取在线圈中心轴线上时，仅存在方向上的磁场．由于近轴区磁场分布的影响，有限元仿真所得轴和轴方向上的磁场在很小的范围内呈高频上下浮动，在忽略影响因素的情况下，同样仅存在方向上的磁场．

图7给出了场点路径选取位于面内(即＝90°)，以转子球心为圆心，半径为80,mm(即＝80,mm)，取值范围为－90°到90°的半圆时，解析法和有限元法所得磁通密度各分量对比．

从图7中可以看出，由于柱形定子线圈关于面对称，且所研究的磁场路径位于面内，因此，方向上的磁场以定子线圈中心轴线为对称轴呈轴对称分布；方向上的磁场以定子线圈中心点为对称点，呈中心对称分布；方向上的磁场为零．

图8给出了场点路径选取为面内(即＝0°)，以转子球心为圆心，半径为80,mm(即＝80,mm)，取值范围为0°到180°的半圆时，解析法和有限元法所得磁通密度各分量对比．

从图８中可以看出，由于柱形定子线圈既关于面对称，又关于面对称．所以，当所研究的磁场路径位于面内时，方向上的磁场以定子线圈中心轴线为对称轴呈轴对称分布；方向上的磁场以定子线圈中心点为对称点，呈中心对称分布；方向上的磁场为0．

综上，有限元结果和解析法结果几乎吻合，对比结果表明，在误差允许范围内，该解析方法是有效的.

图9给出了场点路径选取在定子线圈的中心轴线上，电机转速分别为1,000,r/min、300,r/min、＝50,r/min时的磁通密度B分量对比．

从图9中可以看出，电机转速分别为1,000,r/min、300,r/min、50,r/min时，定子线圈磁场分布曲线基本重合，电机转速对定子线圈磁场分布的影响较小．

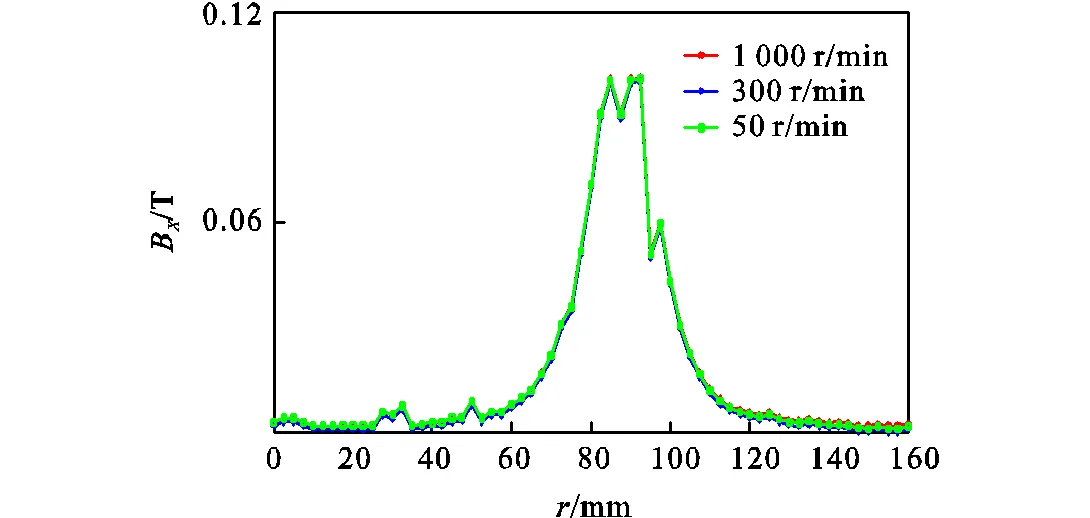
图9 场点在线圈中心轴线上时不同电机转速下的BX分量磁场分布

4 结 语

本文基于毕奥-萨伐尔定律首先求解了任意位置单匝线圈在空间任意点产生的磁场，并与现有文献[22-25]结论相比较，验证了求解思路的正确性．在此基础上，进一步求解得到了任意位置多层多匝线圈在空间任意点的磁场解析表达式．最后就定子线圈在不同路径下的磁场分布与有限元结果进行了对比，证明了本文所得多层多匝线圈磁场分布解析表达式的有效性，为结构复杂的永磁电机定子线圈磁场的研究拓宽了思路．

［1］ Li W，Cao Z，Cheng P，et al. Influence of magnetic wedge on electromagnetic field distribution of permanent magnet traction motor[C] //，，. Aachen，Germany，2015：1-5.

［2］ Wang L，Zhang L，Xu M. Simulation analysis on the influence of magnetic field distribution caused by motor spindle air-gap[C] //. Harbin，China，2011：215-218.

［3］ Zhu Z Q，Howe D，Chan C C. Improved analytical model for predicting the magnetic field distribution in brushless permanent-magnet machines[J].，2002，38(1)：229-238.

［4］ Kajikawa K，Uchida Y，Nakamura T，et al. Development of stator windings for fully superconducting motor with MgB2wires[J].，2013，23(3)：5201604-5201604.

［5］ Li L，Cao J，Kou B，et al. Design of the HTS permanent magnet motor with superconducting armature winding[J].，2012，22(22)：5200704-5200704.

［6］ Zhao J，Shi G，Du L. Miniaturized air-driven planar magnetic generators[J].，2015，8(10)：11755-11769.

［7］ Cukovic J P，Klopčič B，Dolinar D. Analysis of stator winding tester for AC machines[J].，2012，88(7)：16-19.

［8］ Lemmens J，Mulier K，Driesen J，et al. Efficiency improvement of a high dynamic BLDC linear motor by multiphase control[C] //. Denver，USA，2013：1191-1196.

［9］ Xu J，Ma W，Lu J，et al. Analysis of magnetic field distribution and parameter calculation of linear induction motor with novel winding construction[C] //(). Rome，Italy，2010：1-6.

［10］ Wu L J，Zhu Z Q，Staton D，et al. Analytical model for predicting magnet loss of surface-mounted permanent magnet machines accounting for slotting effect and load [J].，2012，48(1)：107-117.

［11］ Han S H，Jahns T M，Zhu Z Q. Analysis of rotor core eddy-current losses in interior permanent magnet synchronous machines[J].，2010，46(1)：196-205.

［12］ Wu L J，Zhu Z Q，Staton D，et al. Analytical modeling and analysis of open-circuit magnet loss in surface-mounted permanent-magnet machines[J].，2012，48(3)：1234-1247.

［13］ Wu L J，Zhu Z Q，Staton D，et al. Analytical model for predicting magnet loss of surface-mounted permanent magnet machines accounting for slotting effect and load [J].，2012，48(1)：107-117.

［14］ Ishak D，Zhu Z Q，Howe D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole[J].，2005，41(9)：2462-2469.

［15］ Zhao N，Zhu Z Q，Liu W. Rotor eddy current loss calculation and thermal analysis of permanent magnet motor and generator[J].，2011，47(10)：4199-4202.

［16］ 吴立建，王群京，杜世俊，等. 磁场积分法在永磁步进球形电动机场分析中的应用[J]. 中国电机工程学报，2004，24(9)：192-197.

Wu Lijian，Wang Qunjing，Du Shijun，et al. Application of magnetic field integral method in the analysis of permanent magnet stepping spherical motor[J].，2004，24(9)：192-197(in Chinese).

［17］ 祝胜涛. 基于有限元法的永磁球形电动机暂态特性分析[D]. 天津：天津大学电气与自动化工程学院，2012.

Zhu Shengtao. Transient characteristic analysis of the permanent magnet spherical motor based on finite element method[D]. Tianjin：School of Electrical Engineering and Automation，Tianjin University，2012(in Chinese).

［18］ 李斌，刘超，李洪凤，等. 永磁球形电机定子绕组的永磁体模型及磁场分析[J]. 天津大学学报，2012，45(11)：1024-1029.

Li Bin，Liu Chao，Li Hongfeng，et al. Permanent magnet model and magnetic field analysis of the permanent magnet spherical motor stator windings[J].，2012，45(11)：1024-1029(in Chinese).

［19］ 李洪凤，沈彦波. 永磁球形电动机永磁体涡流损耗分析[J]. 电工技术学报，2015，30(12)：268-275.

Li Hongfeng，Shen Yanbo. Permanent magnet eddy current loss analysis of the permanent magnet spherical motor[J].，2015，30(12)：268-275(in Chinese).

［20］ 朱平. 圆电流空间磁场分布[J]. 大学物理，2005，24(9)：13-17.

Zhu Ping. Space magnetic field distribution of circular current[J].，2005，24(9)：13-17(in Chinese).

［21］ 张德根，张波. 圆电流和亥姆霍兹线圈磁场的数值模拟[J]. 皖西学院学报，2014，30(2)：39-44.

Zhang Degen，Zhang Bo. The numerical simulation of magnetic field of circular current and Helmholtz coil[J].，2014，30(2)：39-44(in Chinese).

［22］ 曾令宏，张之翔. 圆环电流的磁场以及两共轴圆环电流之间的相互作用力[J]. 大学物理，2002，21(9)：14-16.

Zeng Linghong，Zhang Zhixiang. The interaction force between magnetic field generated by ring current and two coaxial ring current[J].，2002，21(9)：14-16(in Chinese).

［23］ 向裕民. 圆环电流磁场的普遍分布[J]. 大学物理，1999，18(1)：14-17.

Xiang Yumin. The widespread distribution of the ring current magnetic field[J].，1999，18(1)：14-17(in Chinese).

［24］ 张星辉. 圆电流磁感线的分布及磁感应强度的函数表达式[J]. 大学物理，2006，25(1)：32-37.

Zhang Xinghui. Distribution of circular current magnetic induction line and function expression of the magnetic induction intensity[J].，2006，25(1)：32-37(in Chinese).

［25］ 邰显康，云月厚，李国栋. 用级数拟合求圆电流磁场解析解[J]. 大学物理，2003，21(3)：6-8.

Tai Xiankang，Yun Yuehou，Li Guodong. Circular current magnetic field analytical solution based on series fitting[J].，2003，21(3)：6-8(in Chinese).

(责任编辑：孙立华)

Magnetic Field Analysis of the Hollow Stator Coil in Permanent Magnet Spherical Motor

Li Hongfeng1，Li Tianmeng1，Han Bing2

(1. School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China；2.State Grid Tianjin Power Maintenance Company，Tianjin 300230，China)

Permanent magnet spherical motor stator coils are of hollow cylindrical structure．Stator coils are formed by multiple wires wrapping cylindrical aluminum core and distributed independently on the intersection of longitude line and latitude line on the inner wall of the stator spherical shell．In view of the centralized winding structure characteristics of the stator coils，based on Biot-Savart law，and given the influence of the actual position relationship between spherical motor stator coils and stator coordinate system on the complexity of problem analysis，the magnetic field distribution of single turn coil at any position in any space is obtained in this paper and it is verified by comparing with the existing literature．Then，single turn coil is extended to multilayer turns coil and the magnetic field distribution of multilayer turns coil at any position in any space is obtained．Finally，the analytical method in this paper is compared with finite element method in terms of magnetic field distribution on different paths to verify the effectiveness of the proposed analytical method.

permanent magnet spherical motor；Biot-Savart law；magnetic field distribution of stator coil；finite element method

10.11784/tdxbz201701030

TM351

A

0493-2137(2018)01-0064-09

2017-01-25；

2017-07-15.

李洪凤（1979—  ），女，博士，副教授.

李洪凤，lihongfeng@tju.edu.cn.

国家自然科学基金资助项目(51677130).

the National Natural Science Foundation of China(No.,51677130).