基于问题驱动理论的概念课教学设计—以弧度制概念教学设计为例

广东省广州市东涌中学(511453) 何嘉驹 吴敏

一、引言

本文探索了怎样在数学应试与素质教育之间寻找平衡点,以弧度制概念课教学设计为例,阐述了怎样开展问题驱动概念课的教学.本文广州市十三五课题关于教学效能课题研究的开端,也是我们探索问题驱动原理对于概念课教学的尝试,我们会深入研究问题驱动教学理论,并逐步把他应用到概念课、原理课、解题课和复习课中.

弧度制是高一下学期必修四第一章讲授的内容,通常只介绍弧度制与角度制的互换规律,课程标准中对弧度制的要求不高.如何把弧度制概念引入到实际教学中?如何阐明弧度制与角度制概念之间的关系?学生要达到怎样的学习目标?很多老师好像对这类问题是不关注或不了解的.于是学生只是盲目的接受老师灌输的新的数学技能方法,而不知道学习该知识的历史价值与意义,学习数学能给我们带来什么,不得不说这与我们传统的教学注重方法与技巧、忽视思想息息相关.

数学概念的引入大多来源于现实或自然科学中出现的问题.可以这么说,具有促使这个概念产生的最初的问题,这类问题通常称为本原性问题,但是如果是违背概念产生的情景,这类问题通常称为伪命题.笔者认为,概念课教学应该围绕着本原性问题展开,历史上促使一个概念产生的原因是什么?而不是老师凭主观臆想设计一些伪问题、创造一些伪情境.所以问题驱动理论的教学正是探索如何还原数学的本原性问题,让数学问题更具有真实性,激发学生学习数学内驱力.

二、弧度制的历史简介

据我们了解,第一类老师按照人教材P6所述先利用长度有不同的单位米、英尺、码,重量有千克,磅等不同单位,而且不同单位能为我们带来方便,类比方法得到或许我们角的度量也许有不同的单位?进而就产生了弧度制,作为角的度量另一种表示单位;第二类老师根据人教版教材P8例三所述,采用弧度制时,弧长公式与扇形面积公式简单了,从而产生弧度制;第三类老师回顾完初中角度制定义后,马上引入高中有一种新的角度量方式弧度制,并把π=180°就是弧度制和角度制的互换公式告诉学生,完全没有提及弧度制的产生历史.

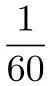
不难发现弧度制的产生与三角函数有紧密关系,弧度制因描述三角函数的不方便而形成.因为在一个三角圆中以角度与弧长两种单位刻画同一数学对象而带来不便,为此需要统一单位,欧拉提出了以半径为单位来量弧长,从而解决了三角函数中一个等式两侧度量单位不一致的麻烦.常常被教师敷衍而过的是一个对后世深远影响的数学概念,这既不符合历史也没有阐明弧度制的重要性体现在哪里.

三、弧度制的教学设计

杜威教育理论认为,教育即生长、教育即生活、教育即经验.我们要善于在学生的生活情景中寻找符合数学发展史的数学本原性问题.从大量的弧度制教学案例中发现,往往新课引入时,教师不是直接通过长度和质量有不同度量方式进行类比,就是从采用弧度制后,弧长公式与扇形面积公式变简单了引入,然后揭示弧度制概念.可是没有告诉学生为什么要研究它,为什么要在本来就有角度制的基础上研究弧度制.这样的教学忽视了两个至关重要的问题：

(1)弧度制来自什么?虽然教材及教参对其历史多有提及,但都是蜻蜓点水带过,很不清晰,学生听了依然对弧度制的发展里程很不清晰;

(一)引入

探究1 同学们大多数都坐过公共汽车来上学,公共汽车里程表记录了公共汽车所行驶的路程,里程表数和车轮之间是否存在一定关系,如果把车轮的半径看作单位1,你知道里程表上的数字和车轮之间的关系吗?(图1和图2)

图1

图2

图3

点评 在没有学习弧度制概念的情况下,学生是解决不了该问题.而该问题正是揭示弧度制概念的本原性问题,即探究里程表上数字和车轮之间的关系,就是探究如何把车轮的旋转运动转化为里程表上表征汽车做直线运动路程的关系(图2,图3),即是探究半径为1的圆.在射线AB上的旋转量.刻画车轮与里程表之间关系需要我们先认识与探究三角学中刻画三角函数发展历史中的故事.

(二)揭示数学史

引起学生的求知欲后,老师可以再给学生揭示弧度制的数学发展里程.

(三)探索概念生成

探究2 你能发现sin30°=0.5等式中左右进制和单位有什么特点?如果你能发现问题所在,你想如何解决它?

点评 学生比较容易想到,在等式sin30°=0.5中,等式左边是以60进制,等式右边是以10进制为单位.等式左边是以弧长为单位,等式右边是以半径为单位.

探究3 学生觉得三角函数等式的两侧单位不一致会带来什么后果?如何解决这个问题?

学生不难想到单位不统一的两个数学对象不能放在等式的左右两侧,所以需要统一单位.

点评 统一单位是解决这个问题的核心,具体来说阿耶波多的正弦表设计按60进制,整个圆周长是2πr=360度 =21600分.假如半径使用弧长的“分”为单位,不难算出：半径约等于3437分.阿耶波多的思想就孕育着弧度制的思想.

探究4 阿耶波多明显是用弧长来表示半径,你们觉得取半径为3438分方便吗?如果不方便,能不能换个角度思考一下?

学生不难想到,用半径去表示弧长,设半径等于1,那么整个圆周的长就是2π个半径,半圆周的长就是π个半径.

探究5 每个小组发一个硬纸做成的圆形图片(图4),一段细铁丝,让学生测量在不同的圆中,等于半径长的圆弧所对圆心角?并且是不是所有同样的圆心角所对的弧长与半径之比都是常数?通过观察所得到的结果有什么规律?并完成下表.

图4

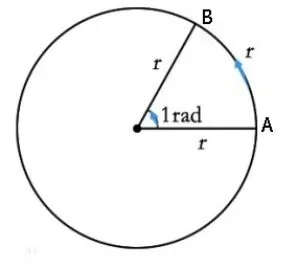
图5

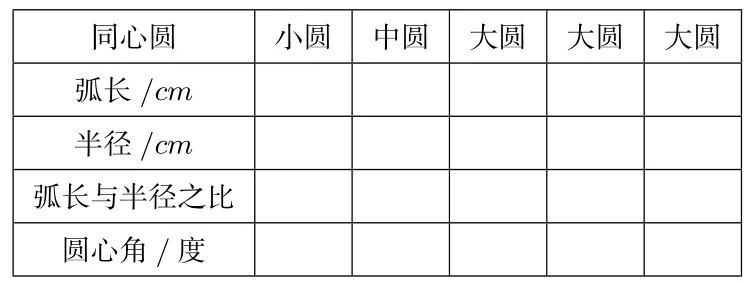
同心圆小圆中圆大圆大圆大圆弧长/cm半径/cm弧长与半径之比圆心角/度

学生通过动手实践,探索发现弧长与半径比值相等,学生还发现了同心圆中同样的圆心角所对的弧长与半径之比是一个常数,而且该常数与圆心角的度数比值相同.

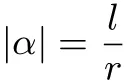
探究6 角度制与弧度制能否换算,如何换算?

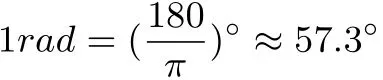
图6

学习了弧度制的概念之后学生就能轻松解决探究1.

(四)拓展提升

即时训练

(1)把下列各角从弧度化为度.

(2)把下列各角从度化为弧度.

拓展 弧度制的实质上说的是实现了弧长与半径的单位统一,那么亲爱的同学们,你们尝试一下完成这条问题：航海罗盘的圆周被分成32等份,把每一等份所对的圆心角的大小分别用度与弧度表示出来?

点评 通过以上例子说明如何运用弧度制解决实际或熟悉问题,这对于激发学生学习动机,以及对弧度制的重要性的认识有很大帮助.为了强化理解概念,必要的练习还是不能少,让学生学会探索问题,掌握解决问题的方法.

四、总结

基于问题驱动的弧度制概念的教学设计,通过查看相关书籍发现弧度制的发展过程,找到弧度制产生的历史事实,找出发展弧度制的本原性问题,利用本原性问题联系学生生活情景,创设弧度制产生的现实问题情境引入.我们可以发现,在数学课堂中引用重现数学概念的历史发展,同时也为学生提供现实创设这数学概念的情境.是能让这节弧度制概念课上活,能让学生感受数学概念创作的伟大,是一碗很好的心里鸡汤.