基于Simulink/CarSim的磁流变悬架预瞄模糊控制

邹 斌，熊 辉，李超群，刘 康

（武汉理工大学 现代汽车零部件技术湖北省重点实验室 汽车零部件技术湖北省协同创新中心，武汉 430070）

随着车辆技术的不断发展，人们对车辆各项性能的要求越发严格。由D.A.Croshy和D.C.Karnopp在1973年首先提出的半主动悬架系统[1]，能够实时调节阻尼或刚度来产生良好的悬架控制力从而有效提高车辆的乘坐舒适性与行驶安全性。由于磁流变液性能稳定可靠、阻尼连续可调且响应迅速等优势，使得磁流变半主动悬架系统成为当前悬架系统领域研究的热点。

磁流变减振器具有巨大潜力，国内外很多学者对其进行了深入的研究，如Lord，Ford，德尔福公司以及京西重工[2]等汽车公司。同时，学者们在天地棚阻尼控制、最优控制、鲁棒控制、自适应控制、滑模非线性控制、智能控制等半主动悬架控制策略方面也做了大量研究工作[3]。

预瞄控制作为一种较新的悬架控制方法，将未来道路信息用于控制策略中，能够有效解决控制滞后问题，从而提高控制效果[4]。考虑到目前很多仿真研究工作基于理想简单的二自由度1/4车辆模型、四自由度1/2半车模型、七自由度整车模型为车辆动力学模型，以及二维路面时域模型为路面输入模型[5-7]，在此利用专业车辆动力学软件CarSim中的整车动力学模型以及基于标准路面不平度模型的CarSim三维道路模型为仿真研究基础，结合模糊控制与轴距预瞄控制，以前悬架感受到的路面信息作为后悬架的前馈控制信息，与反馈控制并行控制，有效抑制车辆簧载质量的振动、减振器动挠度以及轮胎动变形，实现车辆的乘坐舒适性与行驶安全性的优化。

1 磁流变减振器模型

由于磁流变减振器具有很强的非线性，很难建立与实际器件完全相符的模型。考虑到基于Bouc-Wen模型的现象模型能够很好地描述磁流变减振器的动态性能，且比较灵活，优于其他模型[8]，故使用现象模型对磁流变减振器进行建模。

Spencer等提出的现象模型[9]结构如图1所示，其数学模型为

式中：F为模型输出阻尼力；c0为高速时的黏滞阻尼系数；c1为低速时的黏滞阻尼系数；x为减震器活塞杆的位移；k0为高速时的控制刚度；k1为磁流变阻尼器的蓄能器刚度；x0为弹簧k1的初始位移；α，γ，n，β，A为磁流变减振器模型调节参数；z为滞变位移。 其中，α0，c0，c1与磁流变减振器输入电流呈函数关系。

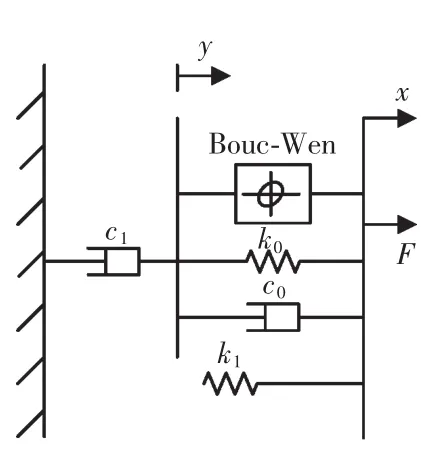
图1 基于Bouc-Wen模型的现象模型结构Fig.1 Structure of phenomenological model based on Bouc-Wen model

在Simulink中建立基于现象模型的磁流变减振器模型，电流范围取0～1 A，正弦激励振幅取±0.03 m，频率取2 Hz，所建立的磁流变减振器模型随电流变化的外特性曲线如图2所示。

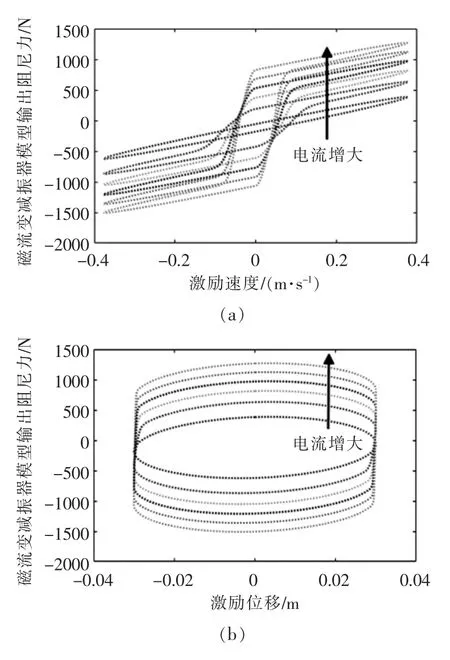
图2 基于现象模型的磁流变减振器模型外特性曲线Fig.2 Outer characteristic curve of MR damper model based on the phenomenological model

由图可见，当激励信号振幅与频率为定值，激励速度相同时，模型输出阻尼力随电流的增大而增大；激励位移相同时，阻尼力也随电流增大而增大。同时，模型较准确地描述了滞回现象，低速时滞回环较大，高速时滞回环较小。应用此模型可以很好地模拟磁流变减振器各阶段的动态行为，其有效性已经在Lord公司的RD21000型磁流变减振器上得到验证。

2 随机路面输入模型

式中：n为空间频率；n0为参考空间频率，一般取n0=0.1 m-1；Gq（n0）为参考空间频率 n0下的路面功率谱密度；W为频率指数，一般取W=2。

根据车速u，将空间频率功率谱密度Gq（n）换算为时间频率功率谱密度Gq（f），空间频率与时间频率关系为

将式（3）带入式（2），得

路面不平度主要采用路面功率谱密度来描述其统计特性[10]。功率谱密度的拟合表达式为

路面不平度时域仿真模拟方法主要有滤波白噪声生成法、AR/ARMA模型法、FFT逆变换生成法以及谐波叠加法等[11]。在此，采用谐波叠加法建立B级三维路面模型，其可行性在文献[12]中得到验证。一般地，路面空间频率n=0.011～2.83 m-1，在常用车速u=10～30 m/s下，对应的时间频率范围为f=0.33～28.3 Hz。将此范围内的时间频率f等分为N=200段，取每小段中心频率fmid，i处的功率谱密度值Gq（ fmid，i）来取代此小段的 Gq（ f），则在时间域内用谐波叠加法模拟随机路面不平度为

式中：θi为［0，2π］内的随机数；q（t）为时域内的路面高程；t为某车速下的时间历程；▽fi为每小段频率长度。将时域模型转换为空间域模型

式中：x，y 分别为路面纵、横向行程；q（x，y）为空间域内的路面高程；θi（x，y）为［0，2π］内的随机数。 取车速u=20 m/s，在Matlab中建立的区域标准B级三维路面模型如图3所示，并将此模型数据写入Car-Sim路面文件，生成CarSim路面模型。

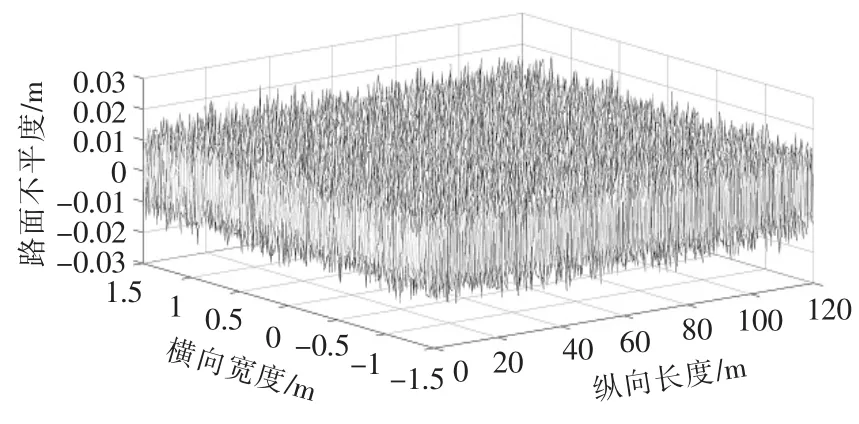
图3 B级路面三维路谱Fig.3 3D road surface of class B pavement

3 轴距预瞄模糊控制器设计

预瞄控制最早由Bender提出[13]，是将悬架前面的路面信息（预瞄信息）用于控制策略，从而提高悬架系统性能的方法。预瞄控制可分为车前预瞄和轴距预瞄，前者利用车前传感器来获取道路预瞄信息，后者利用前轮感受到的路面信息作为后轮的预瞄信息。相比而言，轴距预瞄所需要的传感更少，性价比更高，更具有可行性。轴距预瞄基于汽车直线行驶时，后轮的路面输入与前轮几乎相同，仅存在一个时间差Δt=L/u，式中：L为轴距。

由于模糊控制具有建模简单、处理非线性系统适应性强以及控制精度高等优点，因此已被广泛运用于半主动悬架系统的控制当中[14]。

在此，基于轴距预瞄控制和模糊控制理论，结合CarSim整车动力学模型，建立了磁流变悬架控制系统。其中，前悬架系统采用反馈模糊控制，考虑到控制目标为垂直加速度以及减振器压缩速度与阻尼力密切相关，因此以前减振器压缩位移与压缩速度作为前悬架模糊控制器的输入，输出为磁流变减振器所需电流。对于后悬架系统，采用预瞄模糊前馈控制与反馈模糊控制相结合的控制方法，前馈控制以前轴的位移传感器信息，即延时后的前轴垂向位移及速度作为预瞄模糊输入信号，输出为前馈控制电流；反馈控制以后减振器压缩位移与压缩速度作为输入信号，输出为反馈控制电流。所建立的磁流变悬架控制系统框架如图4所示。

所设计的模糊控制器均采用Mamdani推理方法，去模糊化采用面积重心法。反馈模糊子集的隶属度函数采用高斯函数，前馈模糊子集的隶属度函数采用三角函数，通过悬架的多次仿真分析选取各变量论域及量化因子。用7个语言模糊集来描述输入输出量。 其中， 输入量分为 NB，NM，NS，ZO，PS，PM，PB；输出量分为 VS，RS，S，M，L，RL，VL。其隶属度函数如图5所示。

图4 基于CarSim的磁流变悬架轴距预瞄模糊控制系统Fig.4 System of wheelbase preview fuzzy controller for magnetorheological suspension based on CarSim

图5 反馈模糊隶属度函数Fig.5 Feedback fuzzy membership function

反馈模糊控制器输入为减振器压缩位移及压缩速度，输出为减振器电流。其模糊规则见表1。

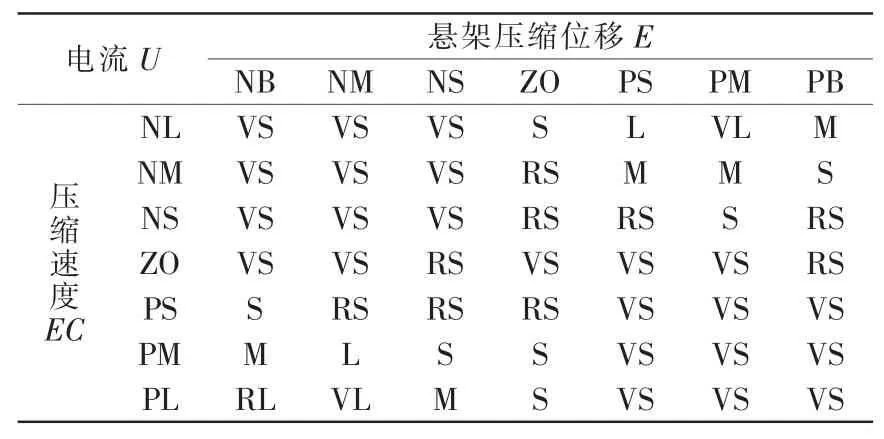
表1 反馈模糊控制器规则Tab.1 Feedback fuzzy controller rules

预瞄模糊前馈控制器的输入为前轴垂向位移信号及其速度信号，模糊控制器的输入、输出隶属度函数如图6所示。

图6 前馈预瞄模糊隶属度函数Fig.6 Feedforward preview fuzzy membership function

建立两输入的模糊控制器的49条模糊规则见表2。

表2 前馈模糊控制器规则Tab.2 Feedforward prerview fuzzy controller rules

4 联合仿真分析

作为车辆动力学与控制领域的前沿课题，汽车悬架控制系统的研究与开发离不开高性能的仿真研究。CarSim作为专业的车辆动力学仿真软件，相比二自由度1/4车辆模型、四自由度半车模型以及七自由度整车模型，更接近于真实车辆，能够有效可靠地对车辆平顺性、操纵稳定性等进行仿真。所建立的CarSim整车模型主要参数见表3。

表3 CarSim整车模型主要参数Tab.3 Main parameters of CarSim whole

建立包括4个减振器压缩速度及压缩位移、4车轮中心垂向位移及垂向速度、簧载质量质心垂向加速度等在内的CarSim到Simulink的输出接口参数，CarSim输入参数为4个减振器阻尼力，用以进行联合仿真控制。在轴距预瞄模糊控制器的基础上，加入所建立的磁流变减振器模型、三维道路模型以及CarSim整车动力学模型，最终建立联合仿真模型，如图7所示。

对所建立的联合仿真模型进行仿真研究，Car-Sim车辆模型车速设置为20 m/s，仿真时间为6 s，三维道路模型为B级道路，以针对车辆的乘坐舒适性和行驶安全性的车身质心垂向加速度、俯仰角加速度、减振器动挠度、轮胎变形量作为评价指标。为了对比研究，在相同的仿真环境下分别对被动悬架、模糊控制悬架进行仿真研究，最终得到的被动悬架、模糊控制悬架、预瞄模糊控制悬架的车辆质心垂向加速度、俯仰角加速度、减振器动挠度、轮胎变形量的时域曲线如图8-图10所示。

图7 基于CarSim/Simulink的磁流变悬架联合仿真模型Fig.7 MR suspension joint simulation model based on CarSim/Simulink

由仿真结果时域曲线可见，相对于被动悬架系统，模糊控制与轴距预瞄模糊控制的磁流变悬架系统在车身垂向加速度、俯仰角加速度、悬架动挠度以及轮胎动变形方面均有所改善。对比被动悬架、模糊控制悬架、预瞄模糊控制悬架3种悬架系统下的仿真结果数据如表4，表5所示。

由表4可知，与被动悬架系统相比，模糊控制悬架系统车身的垂向加速度均方根值及峰值、俯仰角加速度的均方根值分别降低了16.25%，30.88%，13.63%，而俯仰角加速度的峰值虽有所降低，但不明显。轴距预瞄模糊控制悬架与被动悬架相比较，前者的车身垂向加速度均方根值及峰值分别降低了28.45%，37.51%；俯仰角加速度均方根值及峰值分别降低了27.41%，15.25%；不同程度地优于模糊控制的控制效果，提高了车辆的乘坐舒适性。

图8 车身加速度的时域响应Fig.8 Time domain response of vehicle body acceleration

图9 悬架动挠度的时域响应Fig.9 Time domain response of suspensions dynamic deflection

图10 轮胎动变形的时域响应Fig.10 Time domain response of tires dynamic deformation

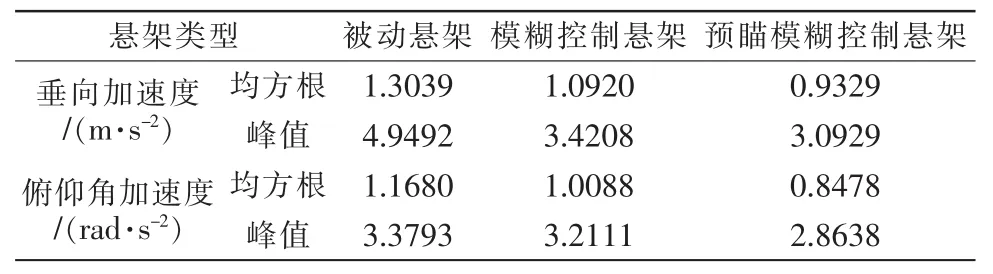
表4 乘坐舒适性数据比较Tab.4 Comparison of ride comfort data

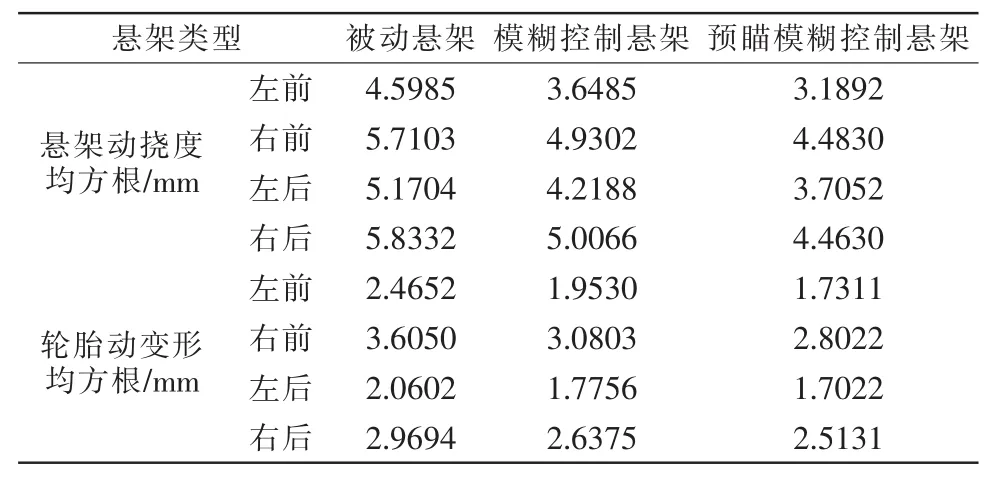
表5 行驶安全性数据比较Tab.5 Comparison of driving safety data

由表5可知，与被动悬架相比，模糊控制及预瞄模糊后整车四悬架动挠度及四轮胎动变形均有所改善。模糊控制悬架四悬架动挠度均方根值分别降低了 20.66%，13.66%，18.40，14.17%；四轮胎动变量均方根值分别降低了20.78%，14.55%，13.81%，11.18%。而轴距预瞄模糊控制悬架四悬架动挠度均方根值分别降低了30.65%，21.49%，28.34，23.49%；四轮胎动变量均方根值分别降低了29.78%，22.27%，17.38%，15.37%；预瞄模糊控制在各方面较模糊控制有更优的控制效果。

仿真结果表明，基于轴距预瞄模糊控制的磁流变悬架系统，较好地改善了悬架系统的综合性能，有效抑制了车身的振动，提高了车辆的乘坐舒适性与行驶安全性。

为了进一步验证仿真模型及控制策略，所建立如图11所示的减速带工况进行仿真研究。

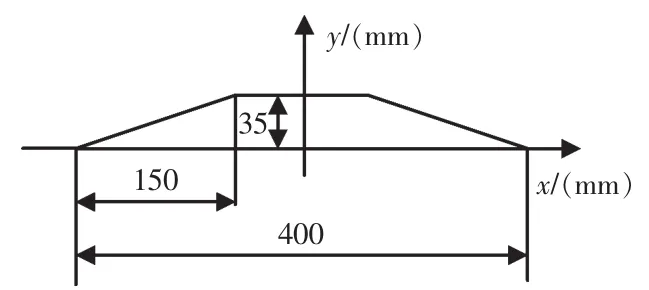
图11 减速带截面Fig.11 Sectional of deceleration belt

车辆模型以10 m/s的速度通过减速带，以相同的仿真环境分别对被动悬架、模糊控制悬架、轴距预瞄模糊控制悬架进行仿真研究，仿真结果如图12所示。

图12 减速带工况下簧载质量垂向加速度衰减Fig.12 Vertical acceleration attenuation of sprung mass under deceleration belt

由图可见，在减速带工况下，相比被动悬架，模糊控制悬架及轴距预瞄模糊控制悬架的簧载质量垂向加速度峰值分别降低了14.49%，23.58%，均能够有效降低簧载质量垂向加速度峰值，并且加快了车身簧载质量的振动衰减。同时，轴距预瞄模糊控制能够在模糊控制的基础上对车身的振动的控制上做进一步改善，有效减缓了减速带对车辆的冲击。

5 结语

利用CarSim与Simulink联合建模仿真的方法，建立了基于现象模型的磁流变减振器模型、更接近于真实车辆的CarSim整车动力学模型以及三维道路模型。基于模糊控制与轴距预瞄控制理论，设计了前悬架模糊控制和后悬架模糊前馈与反馈的轴距预瞄模糊控制的磁流变半主动悬架控制系统。联合仿真结果表明，与被动悬架及模糊控制悬架相比，轴距预瞄模糊控制的悬架在车辆乘坐舒适性方面，车身垂向加速度、俯仰角加速度均有显著降低；在行驶安全性方面，悬架动挠度及轮胎动变形也有明显改善，有效抑制了车身的振动，提高了车辆的乘坐舒适性与行驶安全性。

[1]Karnopp D，Crosby M J，Harwood R A.Vibration control using semi-active force generators[J].ASME Journal of Engineering for Industry，1974，96（2）：619-626.

[2]Savaresi S M.Semi-active suspension control design for vehicles[M].[s.l.]：Elsevier Ltd，2010：9.

[3]朱华.半主动悬架及其控制策略研究综述[J].汽车零部件，2009，4（2）：75-77.

[4]Li P，Lam J，Cheung K C.Multi-objective control for active vehicle suspension with wheelbase preview[J].Journal of Sound and Vibration，2014，333（21）：5269-5282.

[5]贝绍轶，袁传义，陈龙，等.基于轴距预瞄的半主动悬架模糊神经网络控制[J].汽车工程，2010，32（12）：1067-1070，1082.

[6]Wong Pakkin，Xie Zhengchao，Wong Hangcheong，et al.Design of a fuzzy preview active suspension system for automobiles[C]//IEEE System Science and Engineering，Macau，China.2011.

[7]Ahmed M，Svaricek F.Preview control of semi-active suspension based on a half-car model using fast fourier transform[C]//IEEE Systems，Signals&Devices（SSD），Hammamet，Tunisia.2013.

[8]邓志党，高峰，刘献栋，等.磁流变阻尼器力学模型的研究现状[J].振动与冲击，2006，25（3）：121-126，211.

[9]Spencer B F，Dyke S J.Phenomenological model for magnetorheological dampers[J].J of Eng Mech，1997，123（3）：230-238.

[10]余志生.汽车理论[M].北京：机械工业出版社，2009.

[11]吴志成，陈思忠，杨林，等.基于有理函数的路面不平度时域模型研究[J].北京理工大学学报，2009，29（9）：795-798.

[12]李鹏飞，冯国胜，邓晓龙，等.三维虚拟路面的谐波重构[J].汽车工程师，2014，41（11）：24-27.

[13]Bender E K.Optimum linear preview control with application to vehicle suspension[J].ASME Journal of Basic Engineering，Series D，1968，90（2）：213-221．

[14]支龙，昌放辉，陈立平，等.汽车半主动悬架的ADAMS和MATLAB 联合仿真[J].自动化与仪表，2004，24（6）：45-47.