基于VMD的轴承故障定子电流信号诊断

李万涛，时献江

（哈尔滨理工大学 机械动力工程学院，哈尔滨 150080）

轴承是传动部分的一个重要组成，为防止发生轴承损坏引起的严重安全事故，必须对轴承故障的检测加大研究力度，从而保证人民的生命财产安全。因此，对轴承的故障诊断的研究具有很大的意义和发展前景[1]。

目前应用最普遍的就是振动方法来进行故障诊断[2]，可是利用振动方法诊断成本比较高，使得越来越多的研究者开始探索新的故障诊断方式。于是，文献[3]提出了一种无传感器的故障诊断方法定子电流分析法，只需要利用电流互感采集到一些定子电流信号就可以，定子电流法已经逐渐成为一种新的轴承故障诊断方法[4]。目前大多数作者对定子电流信号处理的方法，都集中在使用经验模态分解法[5]，然而EMD算法没有完善的数学理论基础，存在模态混叠、端点效应以及复杂繁琐的计算问题，针对EMD出现的问题，本文引进了变分模态分解法首次对定子电流信号进行分析处理。

变分模态分解法作为一种新兴的能够自适应的对信号进行处理的方法，是由Dragomiretskiy于2014年提出的[6]，它具有非常好的噪声鲁棒性，能够利用迭代搜寻最优解，具有非常扎实的理论算法基础。文献[7]就将变分模态分解法应用于转子碰磨中来检测故障。文献[8]又将其应用在齿轮箱的故障检测中，两者验证了VMD方法的实用性与优越性，因此，本文将VMD方法应用于轴承的故障诊断中。但是，目前大多数作者都使用VMD方法来处理一些振动信号。用来处理其他信号的文献少之又少。故此，本文首创性的提出利用变分模态分解法应用于轴承故障定子电流信号的诊断。

1 VMD方法原理

VMD做为一种新的对信号进行分解的方法，是通过迭代的方式来寻找变分模态模型的最优解，从而确定分解得来的各个模态分量uk。使得uk之和等于原始信号，且分量之间拥有最小的带宽。原始信号经过VMD分解成一系列的VIMF，各个VIMF都被定义成一个调幅-调频信号，也就是：

式中：Ak（t）是 uk（t）的瞬时幅值；Φk（t）做为相位不是一个递减函数；瞬时频率 ωk（t）（ωk（t）=Φk′（t））和瞬时幅值又相对于相位是缓变的。

想要得到各个VIMF的带宽，首先要经过对各个模态进行Hilbert变换来获得边际谱；其次将各个模态的信号经过加入指数项来处理它们预估的中心频率，并且把uk（t）频谱调制到基带上；最后计算解析信号梯度的平方L2范数，估计带宽。变分约束模型如下：

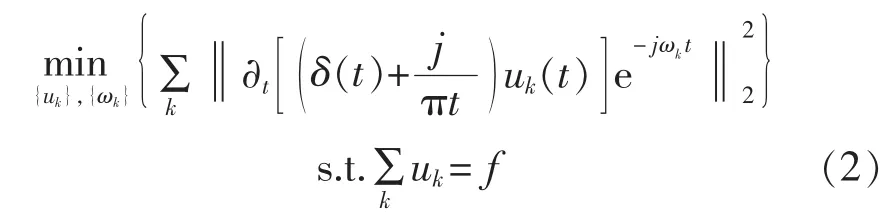
式中：δ（t）为 Dirac 分布；k 为模态分量（k=1，2，3，…，k）；f为原始信号。

为了求得变分约束模型的最优解，引入了二次惩罚因子和Lagrange乘子得到如下表达式：

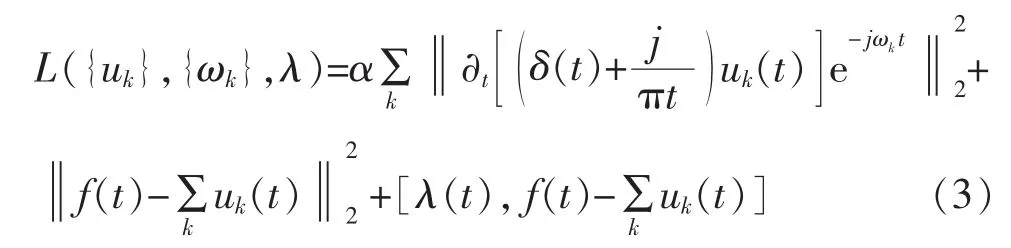
对于上文所求的模型，VMD采用了乘法算子交替的方法，获得了最优解并且把原始信号经过分解得到了K个窄带VIMF。得到这些的具体流程如下：

步骤1初始化｝，λ1和 n 的值；

步骤2使n=n+1，执行循环程序；

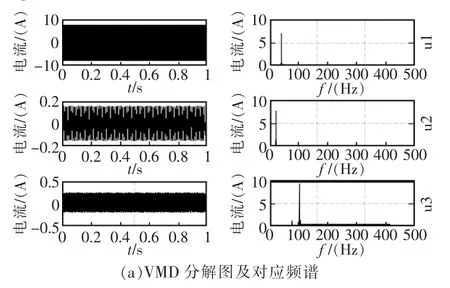
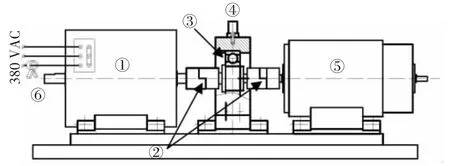
步骤3使k=0，k=k+1，当k

步骤4使k=0，k=k+1，当k

步骤5更新λ为

步骤6重复步骤1～步骤5，到了迭代停止条件就结束循环，得到K个模态分量输出。

2 仿真分析验证

为了能够与实测故障信号做对比，利用Matlab/Simulink软件构建了一个仿真模型，来仿真轴承在故障的情况下定子电流的变化，针对不同情况下的电流信号实行VMD和EMD分析处理，仿真模型如图1所示。

图1 仿真模型Fig.1 Simulation model

在仿真模型中，电机为三相感应电动机，额定功率PN＝4 kW，电压400 V，4极。其它参数如下：定子电阻 Rs=1.405 Ω，转子电阻 Rr=1.395 Ω，定子、转子漏电感Ls1=Lr1=0.005839 H，互感 Lm=0.1722 H。仿真时假定电机和滚动轴承的转动惯量为J=0.02 kg·m2。电机的机械输入为转矩输入，滚动轴承产生的冲击阻力矩具有接触时间短、数值大的特点，因此可以用一个矩形波发生器叠加一个稳定的值来模拟电机的转矩输入，在机械转矩输入端设置一个二位选择开关，用于切换正常状态（稳定负载）或故障状态（变化负载）。在这里，只研究故障状态下的情况。当图中的机械输入选择开关向上时，表示系统扭矩输入为10 N·m加一个矩形波。矩形波主要用于模拟轴承外圈故障引起的周期扭矩波动，根据滚动轴承故障的冲击扭矩计算与分析，矩形波的幅值为 53.67 N·m（计算结果），频率为 73.36 Hz（表 2，外圈故障），由于冲击接触时间较短，无法精确估计，因此暂设脉宽比为1%～2%。

图2为不同处理方法下轴承外圈故障仿真信号所对应的分解信号及对应的频谱，图3为不同方法下对应的包络谱。采集条件是1000 Hz采样，300 Hz低通，采样点数5120点。在采用EMD分解时，只选择了处理后的前4个分量。可以从图2（a）中很容易地看出VMD方法能很好地去除伪分量，并且在对应的频谱图中可以看到提取出了完整的故障特征频率。图2（b）EMD分解的分量分解效果不是很好，存在很严重的模态混叠现象，很多微弱的信号都被埋没在了强信号中。在图3所示的各分量包络谱中，用EMD分解的各个分量对应的包络谱中只有IMF1可以清楚地看到26.56 Hz的转频以及73.44 Hz的故障频率，然而其他分量包络谱中几乎没有故障频率及转频信息。VMD分解的各个分量的包络谱则是特征频率突出，能够清楚看出并进行识别。

图2 不同方法分解后的信号及对应频谱Fig.2 Decomposition and spectrogram

图3 不同方法分解对应包络谱Fig.3 Different methods decomposition corresponding envelope spectrum

3 故障模拟试验

3.1 故障模拟试验装置

滚动轴承故障模拟试验台的主要结构如图4所示，实体照片如图5所示。主要由电动机①、联轴器②、主轴、故障模拟滚动轴承及轴承座③、加速度传感器④、负载发电机⑤和电流互感器⑥等组成。电动机为0.25 kW的三相异步电动机，通过联轴器驱动滚动轴承和单相直流发电机旋转，发电机此时作为负载使用，通过调节负载电阻的阻值可以调节系统的负载。

图4 滚动轴承故障模拟试验台Fig.4 Fault simulation test bench of rolling bearing

图5 滚动轴承故障模拟试验台照片Fig.5 Fault simulation test bench photo of rolling bearing

电流信号检测采用钳形电流互感器，电流互感器输入交流0～10A，输出0～4mA电流信号。电流信号经I/V转换和放大后，经高低通滤波器送到数据采集卡。

试验采用307滚动轴承，有2种制造模拟故障的方法，一种是用线切割方式来模拟外圈故障，如图6（a）所示，也可以采用亚弧焊破坏滚道表面的方法来模拟，如图6（b）所示。由于本文所使用的试验台没有径向加载装置，所以很难保证每次钢球都“掉入外圈故障坑”。而亚弧焊可使滚道表面产生凸凹不平，相当于轴承产生局部点蚀或剥落故障，滚珠通过该区域时受阻，必定每次产生冲击，所以选择图6（b）所示的轴承进行试验。

图6 试验用故障轴承Fig.6 Fault bearing used in experiment

表1为307轴承的主要参数，表2为其转频及故障特征频率[9]，供本文计算和分析之用。

表1 试验用滚动轴承基本参数Tab.1 Basic parameters of rolling bearing for experiment

表2 试验用滚动轴承计算故障频率Tab.2 Calculation of fault frequency with rolling bearing

3.2试验结果对比分析

对于实测故障信号，本文通过对不同方法获得分量中选择最优分量来进行包络谱分析。图7为不同方法下模拟外圈故障时的试验分析结果，数据采集条件为1000 Hz采样，300 Hz低通，采样点数5120点。图7（a）为EMD分解后的第一个分量对应的故障轴承的电流信号包络谱。可以清楚看出轴转频22.66 Hz和外圈故障频率68.75 Hz成分，且外圈故障频率为主要成分；图7（b）为VMD分解后的第四个分量对应故障轴承的电流信号包络谱，主要频率成分及分布和仿真结果基本吻合，主要为外圈故障频率68.75 Hz和转频22.66 Hz及倍频成分。由于在测量的时候可能会有些误差所以计算的故障频率会与包络谱中的特征频率有些误差。

图7 外圈故障模拟试验信号包络谱Fig.7 Simulation of the outer ring fault bearing and the envelope spectrum for simulated experimental signal

通过对比图 7 中的（a）和（b），可知 VMD 分解得到的包络谱能够展示完整的故障特征频率，且避免了模态混叠现象的出现，除了突出转频及故障频率倍率外，包络谱中几乎没有其他成分出现，在高频段无突出成分，能很好地反映故障特征。

4 结语

本文利用定子电流分析法，通过构建发电机与轴承扭矩的联合机电仿真模型，对故障下的轴承进行模拟仿真，采集定子电流信号，利用VMD方法和EMD方法对电流信号进行对比分析处理。同时，搭建试验台，采集在故障下的电流信号分别利用VMD分解法和EMD分解法进行分解，对不同方法分解后的某个分量通过求包络谱来进行对比。结果表明，VMD方法在对定子电流信号分析中能够克服EMD方法在分解中存在的模态混叠和伪分量现象，能够很好的提取出故障频率成分，可以将其应用于轴承故障定子电流信号的诊断中。

[1]唐贵基，王晓龙.基于EEMD降噪和1.5维能量谱的滚动轴承故障诊断研究[J].振动与冲击，2014，33（1）：6-10.

[2]冯志鹏，褚福磊.行星齿轮箱齿轮局部故障振动频谱特征[J].中国电机工程学报，2013，33（5）：119-120.

[3]Kryter R C，Haynes H D.Condition monitoring of machinery using motor current signature analysis[J].Sound and Vibration，1989，（9）：1720-1725.

[4]Z.Daneshi-Fa，G.A.Capolino，H.Henao.Review of failures and Condition Monitoring in Wind Turbine Generators[C].19th International Conference on Electrical Machines，ICEM2010，2010：1-6.

[5]时献江，罗建，宫秀芳.无传感器诊断方法及在风力发电中的应用与展望[J].哈尔滨理工大学学报，2014，19（6）：82-86.

[6]Dragomiretskiy K，Zosso D.Variational Mode Decomposition[J].IEEE Transactions on Signal Processing，2013，62（3）：531-544.

[7]WANG Y，MARKERT R，XIANG J，et al.Research on variationalmode decomposition and itsapplication in detecting rub-impact fault of the rotor system[J].Mechanical System and Signal Processing，2015，60：243-251.

[8]石敏，李影，王冰，等.基于变分模态分解的齿轮箱故障诊断[J].电力科学与工程，2016，32（1）：23-26.

[9]时献江，王桂荣，司俊山.机械故障诊断及典型案例解析[M].北京：化学工业出版社，2013.