基于模糊PID的双容液位过程控制系统研究与试验

刘艳梅，陈 震，陈显伟

（1.沈阳航空航天大学 自动化学院，沈阳 110136；2.辽宁省送变电工程公司，沈阳 110179）

由于二阶双容液位系统具有一定的非线性和时滞性的特点，所以普通PID算法的控制效果并不理想。模糊控制系统在控制方法上应用模糊集合论，运用模糊语言变量及模糊逻辑域实现系统的智能控制[1]。这种方法摆脱了控制对象输入、输出物理量的精确描述，用自然语言描述专家控制策略，以机器模拟人的模糊思维对系统实现有效控制[2]。在实际控制过程中，将计算机采样的输入量（精确量）模糊化，经模糊确定控制量的模糊值，最后进行反模糊处理获得控制量的实际输出，对被控对象进行控制[3]。模糊PID算法是传统PID算法和模糊算法的有机结合，该算法既有模糊算法控制灵活和鲁棒性强的优点，又具有较强的非线性跟踪学习能力，具有一定的实际意义和广阔的应用前景[4]。本文将该算法运用到双容液位过程控制系统中，实现了PID参数的自适应控制，大大提高了控制质量。

1 模糊PID控制器设计

1.1 模糊PID控制器的结构

模糊PID控制器的结构如图1所示。模糊推理系统用来对系统状态变量进行模糊量化处理[5]。利用模糊控制的鲁棒性和非线性控制作用，对作为控制输入的状态变量进行模糊规则的预处理，根据系统的运行状态，自行整定PID参数，以期达到最优的控制效果。也就是将模糊控制的输出对应于PID控制器的3个可调参数Kp、Ki、Kd，通过模糊推理，从而使稳定状态对应于某种最优控制下的PID参数[6]。 直接对控制对象进行闭环控制，并且 Kp、Ki、Kd3个参数为在线整定式。

图1 基于模糊PID的液位串级控制系统结构Fig.1 Level cascade process control system structure based on fuzzy PID

1.2 模糊控制器的设计

模糊控制器的设计步骤：①建立系统的输入和输出变量；②将系统变量模糊化并确定模糊控制器的结构；③模糊规则的建立；④进行模糊推理，建立模糊控制规则表；⑤解模糊。

设定输入变量：综合偏差E，论域设为［-6 6］；综合偏差率 EC，论域设为［-6 6］；输出变量：Kp、Ki、Kd，论域分别设为［-3，3］，［-0.6，0.6］，［-3，3］；每个变量用7个语言变量｛NB NM NS ZO PS PM PB｝来描述，均采用三角型、全交迭、均匀分布的隶属度函数。

模糊控制设计的核心是设计人员的实际操作经验，建立合适的模糊规则表[7]。根据输入/输出论域上的模糊语言变量划分NB（负大），NM（负中），NS（负小），ZO（零），PS（正小），PM（正中），PB（正大），可以设计模糊推理规则如表1～表3所示。模糊控制器设计如图2所示。

表1 Kp的模糊规则表Tab.1 Fuzzy rule table of Kp

表2 Ki的模糊规则表Tab.2 Fuzzy rule table of Ki

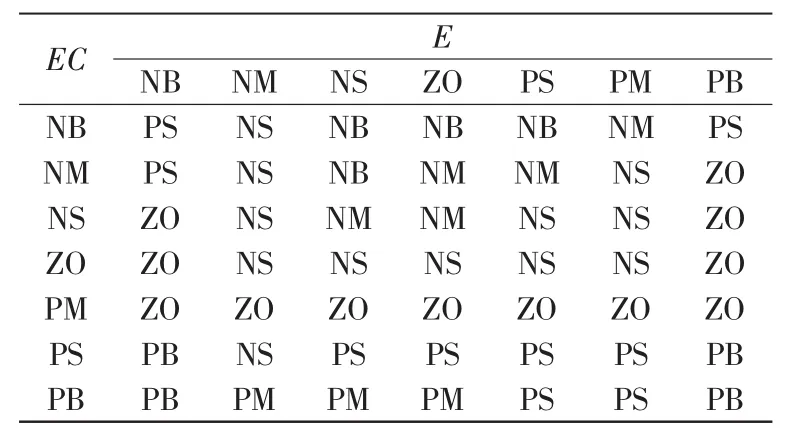
表3 Kd的模糊规则表Tab.3 Fuzzy rule table of Kd

图2 模糊推理界面Fig.2 Fuzzy interference view

建立输入变量的隶属度函数，两个输入变量角度误差E和角度误差变化率EC，论域为［-3，3］，集定义 7 个模糊子集｛NB，NM，NS，ZO，PS，PM，PB｝。如图3所示。

图3 输入变量的隶属度函数曲线Fig.3 Membership function curve of input variables

建立3个输出变量的隶属度函数，输出为3个变量 Kp、Ki、Kd，论域分别为［-3，3］，［-0.6，0.6］，［-3，3］，都定义 7 个模糊子集｛NB，NM，NS，ZO，PS，PM，PB｝。如图4所示。

图4 输出变量的隶属度函数曲线Fig.4 Membership function curve of output variables

2 模糊PID液位串级系统

2.1 液位串级系统

液位串级系统的结构如图5所示。从图中可以看出，液位串级系统针对上水箱液位和下水箱液位两处的干扰，设计成主、副双闭环结构，这样做提高了控制精度和控制效果，但增加了控制难度。在对系统进行调节时，先整定副调节器的参数，当副环稳定后再进行主调节器的参数整定，从而使整个系统达到稳定运行状态。

图5 液位串级系统结构Fig.5 Structure block of level cascade system

2.2 基于模糊PID算法的液位串级控制系统

基于模糊PID算法的液位串级控制系统的结构框图如图6所示。

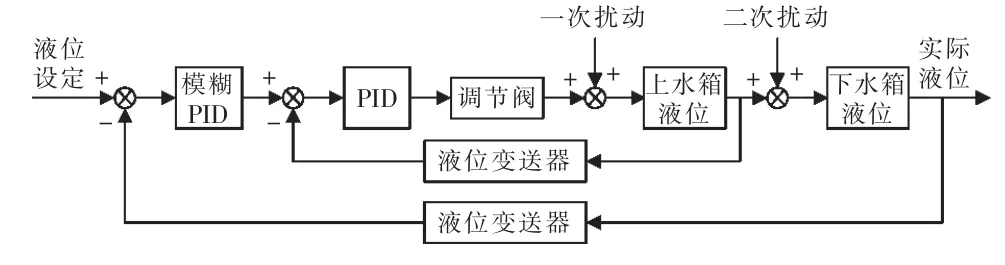
图6 基于模糊PID算法的液位串级控制系统结构Fig.6 Structure block of level cascade system based on fuzzy PID

该系统将模糊PID算法运用到二阶液位的控制过程中，使用模糊控制理论将采集到的系统状态信息模糊化、归一化后的状态变量转化为PID控制器的控制参数，达到对PID参数的优化，以期达到最优的控制目的。

2.3 编程实现

本文所涉及的控制算法由2个部分组成：一是PID算法，它可以根据液位偏差算得电动调节阀的控制量，从而达到对液位的控制；二是模糊算法，用来根据系统的状态变量对PID参数进行调整，以期达到最优控制。具体的编程实现是在组态王6.5的环境下进行的，在组态王环境下编制控制界面，并与Matla进行通讯，用来实现模糊PID算法优化过程，为组态王中的控制过程提供PID参数。两种软件之间的数据交换采用标准DDE连接完成。程序流程图和监控界面如图7、图8所示。

3 试验结果

将本文控制算法在A3000型过程控制系统试验装置上进行在线调试，如图9所示，分别得到了液位串级控制在传统PID算法和模糊PID算法2种不同情况下的性能曲线，如图10和图11所示。

图7 基于模糊PID算法的液位串级控制流程Fig.7 Flow chart of level cascade system based on fuzzy PID

图8 液位串级控制组态监控界面Fig.8 Configuration monitoring interface of level cascade control system

图9 过程控制试验系统Fig.9 Process control experiment system

图10 传统PID控制性能曲线Fig.10 Characteristic curve of PID control system

从图10可以看出，过程有较大超调，控制效果不甚理想。图11是基于模糊PID液位串级控制的性能曲线，其中液位过程的调节时间大大缩短，并且控制精度在误差允许范围内，超调现象较小，控制效果比传统PID算法有了显著的提高。

图11 模糊PID控制性能曲线Fig.11 Characteristic curve of fuzzy PID control system

4 结语

对于液位串级控制系统，由于传统PID算法在参数整定过程中的缺陷，很难满足液位串级系统在精度和动态性能等方面的要求。本文针对以上问题，提出了模糊PID算法，将其运用在液位串级控制系统中，并在A3000型过程控制系统试验装置上进行在线调试。结果表明，模糊PID算法不仅简化了PID参数整定的过程，而且使得液位串级控制系统的性能有了很大改善。比较优化前后的曲线可以看出，该方法可以获得满足工业控制要求的控制曲线，减少了调节时间和动态误差。由此证明本文提出的控制策略和程序实现方法符合实际控制要求，有一定的实际应用价值。

[1]刘建秀，张杨.压电陶瓷精密位移系统的变论域模糊控制法[J].自动化与仪表，2017，32（2）：45-49.

[2]吴晓莉，林哲辉.MATLAB辅助模糊系统设计[M].西安：西安电子科技大学出版社，2002.

[3]陶永华.新型PID控制及其应用[M].北京：机械工业出版社，2002.

[4]张坤，许伦辉.基于模糊控制的AGV差速转向控制算法研究[J].自动化与仪表，2016，31（10）：1-4.

[5]Jianqiang Yi，Naoyoshi Yubazaki.Stabilization fuzzy control of inverted pendulum systems[J].Artificial Intelligence in Engineering，2005，14（7）：153-163.

[6]Jianqiang Yi，Naoyoshi Yubazaki，Kaoru Hirota.Stabilization control of series-type double inverted pendulum systems using the SIRMs dynamically connected fuzzy inference model[J].Artificial Intelligence in Engineering，2005，15（3）：297-308.

[7]Jianqiang Yi，Naoyoshi Yubazaki，Kaoru Hirota.A new fuzzy controller for stabilization of parallel-type double inverted pendulum system[J].Fuzzy Sets and Systems，2006，126（1）：105-119.