大学生方程式赛车后轮转向梯形优化及仿真

张祥勃，何耀华

（1.武汉理工大学 汽车工程学院，武汉 430070；2.现代汽车零部件技术湖北省重点实验室，武汉 430070）

大学生方程式汽车大赛（FSAE）由各国的汽车工程师协会举办，参赛成员为本科生和研究生，其中中国大学生电动方程式可以允许博士生参加，但不得超过3人。大赛的理念是让学生团队模拟一家制造公司开发一种小型方程式赛车。开发的原型赛车是为了评估其产品潜力，包括商业、成本等商业潜力和加速性、稳定性等性能潜力。

赛车转向器作为转向系统的重要组成部分，在行车过程中实现转向功能[1]，其作为改变汽车行驶方向及保持汽车稳定行驶的关键零部件，其性能的优劣直接关系到人身和比赛成绩[2]。赛车动态比赛中，8字绕环、高速避障和耐久赛对赛车转向时的稳定性要求较高。与传统的两轮转向赛车相比，四轮转向赛车在低速时转向半径更小，具有更好的灵活性；在高速时回避障碍物的操纵稳定性响应更好，具有更好的安全性。同时，在《2016中国大学生方程式汽车大赛规则》中明确指出允许后轮转向。在四轮转向中，常见的转向动力实现方式有机械式、电子液压式、电子液压机械式和电动式。其中，电动助力转向控制系统（EPAS）是一种新型的汽车助力转向系统，相对于传统液压动力转向（HPS）系统，它具有节约燃料、有利于环保和可控转向等优点。它通过电动机产生助力来帮助驾驶员转向，一般由机械转向器和电子控制单元组成。汽车转向时，扭矩传感器测得驾驶员的输入力矩，并根据车速信号和光电编码器的转角信号，由控制算法控制助力电机产生助力力矩来帮助转向[4]。若将电动式四轮转向系统和线性比例控制结合，可以实现车辆质心侧偏角为零的设计要求，该系统的另一个优点是前后转向系统之间没有机械及油管连接，布置灵活度较高且系统质量较小[5]。所以本文的四轮转向实现方式选择采用线性比例控制的电动助力转向系统，并对所选的控制策略进行角阶跃响应分析。

1 比赛规则对转向设计的限制

由于比赛规则对设计具有指导和限制作用，所以先将部分与转向有关的规则事先说明[6]。

（1）方向盘必须与前轮机械连接。前轮禁止使用线控转向及电控转向。

（2）允许后轮转向（可采用电控转向方式），但后轮的角位移需要被机械限位装置限制在最大6°范围内。在技术检查中，车手必须坐在赛车中演示，并且车队必须提供设备证明转向的角度范围。

（3）转向齿条必须与车架机械连接。如使用螺栓，必须满足规则中的要求。

（4）连接方向盘和转向齿条的连接件必须通过机械连接，并且在技术检查中可见。不允许使用没有机械支撑的粘接方式。

2 总体布置方案

2.1 整车基本参数

本文设计的摇块式后轮转向梯形基于武汉科技大学赤骥车队2015赛季赛车，优化及仿真所需参数如表1所示。

表1 整车基本参数Tab.1 Basic parameters of the vehicle

2.2 后轮转向电机选型及主要参数

由于无刷直流伺服电机具有体积小、重量轻、精度高、响应迅速、力矩稳定等特点，所以本设计选用电压为12 V的无刷直流伺服电机。电机型号为SMJ无刷直流伺服电机SMP6212，自带行星减速器，减速后的基本参数如表2所示。

表2 电机基本参数Tab.2 Motor basic parameters

2.3 后轮转向器选型

FSAE赛车中一般选用齿轮齿条式转向机构作为前转向器。但是由于后轮的转角比较小，规则限制在6°范围内，如果沿用前转向系统中的齿轮齿条式转向机构，则齿条行程较小，大概在10～20 mm范围。同时由于齿轮齿条配合时有一定间隙，这种间隙在更小的齿条行程中被放大。在另一方面为了简化转向器结构，又保证在小转角的范围内实现阿克曼转向定律，本设计采用一种简单的转向摇块结构。具体结构设计如图1所示。

图1 后轮转向器装配图Fig.1 Rear wheel steering gear assembly diagram

2.4 后转向梯形的布置

本文参考车型的悬架为独立悬架，与之相配的转向梯形是断开式转向梯形，其有4种类型，即前方前置（前方指转向机齿条轴线位于车轴前方，前置是指转向节臂位于车轴前方，以此类推）、前方后置、后方前置和后方后置[7]，如图2所示。为使转向尽可能轻便，而当转向梯形趋近于矩形时，其转向轻便性无疑最优。由于FSAE赛车的布置形式基本都为后置后驱，且基本上都为链传动。所以差速器和大链轮都布置在汽车的后方，两者的轴线和后轴近似同轴。这种情况下，为防止转向电机、转向横拉杆和大链轮、大链轮护板、差速器等干涉，梯形的布置只能为后方后置。如图2（a）所示，总体布置形式如图3所示。

图2 转向梯形的4种布置形式Fig.2 Four kinds of steering trapezoidal form

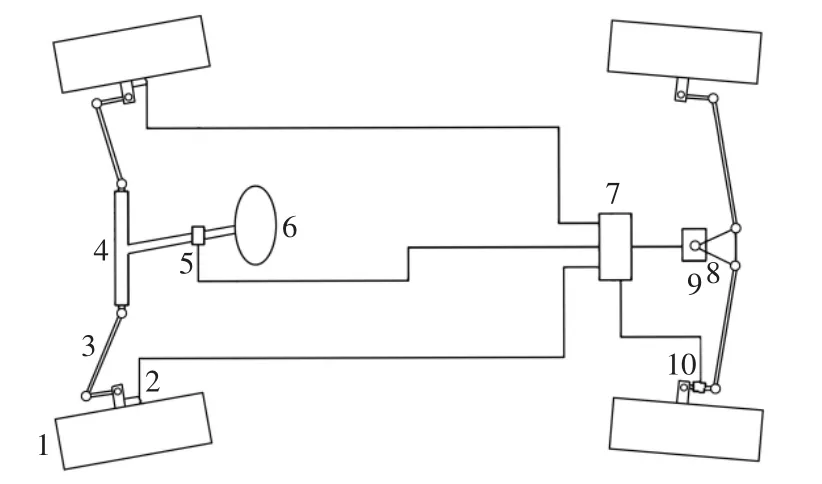
图3 总体布置形式Fig.3 Overall arrangement

3 后轮转向梯形优化

3.1 阿克曼转向几何关系

由于四轮转向时转向半径由前后转角决定，而后轮转角又由前轮转角及车速决定。这样无法单独求出后轮转角与转向中心的相对位置关系。对此引出前后外侧车轮的大致转角关系来解决该问题，后轮理想转角关系如图4所示。由比例控制及前轮转角变化时对应的转向半径关系，可求得[8]：

图4 后轮理想转角关系Fig.4 Ideal rotation angle of the rear wheel

图4中交点O称为转向中心，由图分析得：

由上述公式可以得出理想后内外车轮转向时的角度关系。

以此为基础进行后轮转向梯形的优化。同时考虑轮胎侧偏特性，后轮阿克曼转向梯形百分比取50%，则目标函数为

3.2 后轮转角关系函数

后轮实际转角关系如图5所示。

图5 后轮实际转角关系Fig.5 Actual angle of the rear wheel

当后外侧车轮转角为0时，可以得到中性位置的转向梯形底角为

式中：Lr1是转向摇块底边长度；Lr2是后转向横拉杆的长度（在转向梯形所布置的平面内）；Lr3是后转向节臂的长度；yr是转向摇块上顶点距后轴的距离；c是转向摇块上顶点距转向摇块底边的距离，优化中取52 mm；θz是转向摇块转角；αr是后外侧车轮转角；是后外侧车轮实际转角。

3.3 后轮内外侧车轮转向角误差分析

以上述的数学模型为基础，通过Matlab编写程序的方式实现，图6为优化流程。

图6 优化流程Fig.6 Flow chart of the optimize

3.3.1 确定设计变量和优化目标函数

对于给定的参考车型，其轴距L、轮距B等参数均为定值，因此在优化转向梯形机构时，需要确定的参数分别为转向摇块底边长度Lr1、后转向横拉杆长度Lr2、后梯形臂长度Lr3和转向摇块上顶点距后轴距离yr。

方程式赛车一般均在特定的赛道上行驶，赛车场弯道数量比较密集，且弯道急，驾驶员需频繁转向。统计资料表明，赛车外转向轮频繁的在0°～25°之间变换。因此，为使赛车具有良好的转向性能、驾驶舒适性和较高轮胎寿命等，确定优化的目标转角范围为0°～25°。通过对不同转角使用频率的分析可以得 10°以下的转角使用较为频繁，10°～20°的转角次之，20°以上的转角使用最少。因此为使得转向梯形实际内轮转角尽可能接近理论期望值，取如下加权因子[7]：

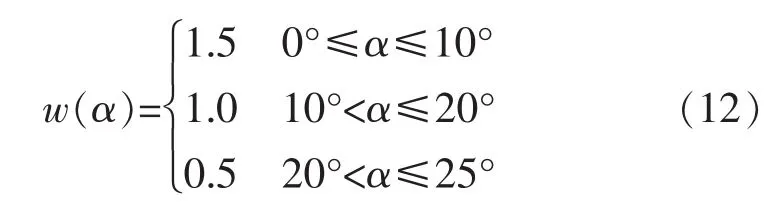
构成评价设计好坏的目标函数 f（x）：

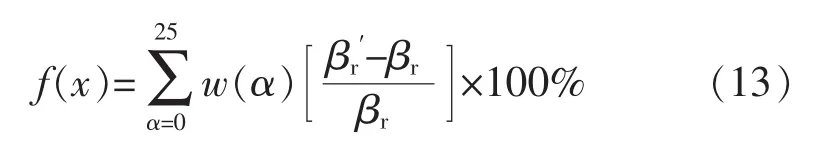
式中，x 是设计变量，x=［x1x2x3x4］T=［Lr1Lr2Lr3yr］T。

使用Matlab优化工具箱里的Fmincon函数，进行多元非线性约束最小值寻优问题的求解。

3.3.2 约束条件

转向梯形各杆件的布置应体现以下基本原则：

（1）因梯形臂主要承受的是弯矩作用，因此转向横拉杆与梯形臂尽可能成90°的夹角，以保证力传递的效果。

（2）转向横拉杆与摇块非底边之间是力传递的关系，因而在传动过程中，两杆之间应尽可能保持小的夹角，以维持两杆间压力角（传动角）在规定的范围内，在优化过程中，将其作为非线性约束，即传动角不小于40°。

（3）防止转向梯形在运动过程中和轮辋、悬架以及制动器干涉。

根据初步设计，取杆件长度（mm）初值分别为Lr1=60，Lr2=535.5，Lr3=70，yr=148。

以下为梯形杆件长度（mm）优化变量的变化范围，即上下限约束：20≤Lr1≤70，500≤Lr2≤560，40≤Lr3≤100，140≤yr≤200。 其中，线性约束为 Lr1+2Lr2≤1250。

在知道目标函数和后轮转角关系函数之后，由传动角不小于40°的要求得出非线性约束条件。值得注意的是在后轮转向梯形的优化中，后轴距转向摇块上顶点距离的下限为140 mm，这是由于防止转向电机与差速器等的干涉造成的。最终的优化结果如表3、图7和图8所示。

从图8可以看出，实际转角关系和目标函数基本一致，最大的误差为0.15°。后轮转向梯形的误差比较大，这是由于约束条件中的值的下限较大，并不是转向摇块转向机构本身的缺陷，原因是由于后轴距转向摇块上顶点距离的下限为140 mm，不能再小的缘故。如果没有该限值，则优化结果会更好。

表3 优化结果Tab.3 Optimization results

图7 理想与实际后内外轮转角关系Fig.7 Relationship between the ideal and the actual internal and external wheel angle

图8 理想与实际后内轮转角误差Fig.8 Ideal and actual inner wheel angle error

4 四轮转向控制策略

4.1 四轮转向的控制方式

四轮转向的前后轮控制方式有很多，主要可分为以下7类[9]：

（1）定前后轮转向比四轮转向系统；

（2）前后轮转向比是前轮转角函数的四轮转向系统；

（3）前后轮转向比是车速函数的四轮转向系统；

（4）具有一阶滞后的四轮转向系统；

（5）具有反相特性的四轮转向系统；

（6）具有最优控制特性的四轮转向系统；

（7）具有自学习、自适应能力的四轮转向系统。

随着研究的深入，越来越多的理论被提出。具有代表性的多目标综合具有较高鲁棒性，但要求测量的因素较多，不适合在FSAE赛车中使用。目前研究的比较多的模型跟踪控制同样需要同时测量多个状态量。虽然提出的算法较多，但没有公认的最优控制，并且对传感器设备等要求较高[10]。

目前，应用于实车上的方法主要是前后轮比例控制关系的控制方法。考虑到可操作性，本设计基于二自由度汽车模型，选择前后轮转角成比例的控制方式进行设计。

4.2 角阶跃输入响应分析

为表征赛车的操纵稳定性，引入角阶跃响应作为评价指标[11]。根据理想二自由度汽车四轮转向模型，可求得汽车横摆角速度和前轮转角的传递函数[12]：

根据此传递函数，求得当前轮角阶跃输入时，汽车横摆角速度的变化。

本次分析设定阶跃信号的起跃时间为0 s，幅值为0.1 rad，取车速40 km/h和80 km/h以观察同向转向和逆向转向的差别。同时引入前轮转向车辆作为对比。从图9中可以看到，在低速（后轮与前轮转角逆向）的情况下，同一速度下的四轮转向车辆的稳态横摆角速度增益大于前轮转向车辆。较大的横摆角速度增益表示转过相同的弯道时，如果转向器角传动比相同，四轮转向车辆比前轮转向车辆要转动更小的方向盘转角[13]。由于赛道具有较多的小半径转向弯道，低速转向情况较多，所以四轮转向车辆比前轮转向车辆少打方向盘，具有更好的操作舒适性。在高速（后轮与前轮转角同向）的情况下，同一速度下的四轮转向车辆的横摆角速度增益小于前轮转向车辆，并且车速越高，差异越明显。同理，高速时，在相同的转向半径下，四轮转向要比前轮转向更多地转动方向盘，但是一般高速时转向的转向盘转角较小所以影响不大。同时，在同一车速下，四轮转向车辆和前轮转向车辆各自到达稳态值的时间大致相同。造成四轮转向车辆和前轮转向车辆横摆角速度增益区别的主要原因是由于后轮转向引起转向半径的改变，进而影响车辆的横摆角速度。

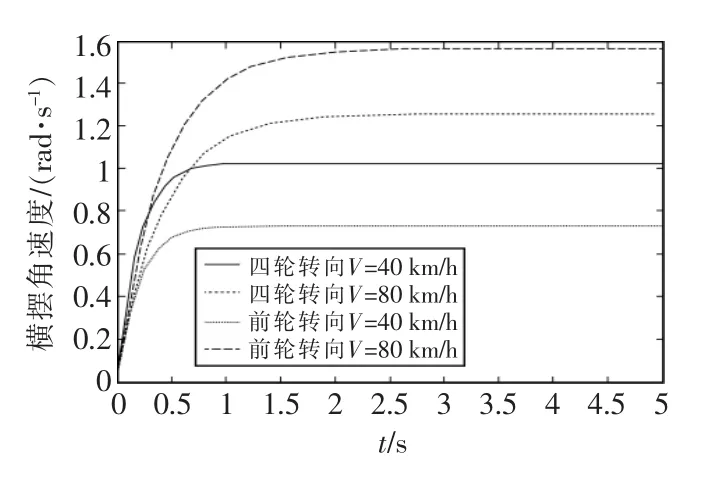
图9 横摆角速度阶跃响应比较Fig.9 Comparison of step response of yaw rate

当前轮角阶跃输入时，汽车质心侧偏角与前轮转角之间的传递函数：

根据该传递函数求得角阶跃输入下，车辆质心侧偏角的变化规律如图10所示。从图中可以看出，四轮转向车辆的稳态质心侧偏角恒为0，车身与行驶轨迹的方向基本一致，所以车辆总是面向其行驶方向，方便驾驶员判断行驶情况，改善了操纵稳定性。前轮转向车辆在低速时，质心侧偏角与转向方向同向，高速时相反。即低速情况下前轮转向车辆有一定甩尾的趋势，高速时有一定侧滑的趋势，均会恶化车辆的操纵稳定性。

图10 质心侧偏角阶跃响应比较Fig.10 Comparison of step response of centroid deflection

汽车侧向加速度与前轮转角之间的传递函数为

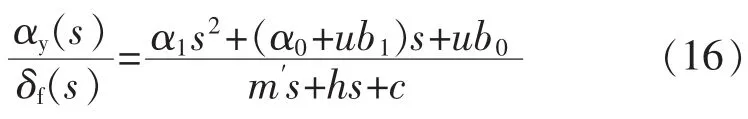
从图11可以看出，在低速情况下，四轮转向车辆的侧向加速度稳态值大于前轮转向车辆，高速情况下相反。并且高速情况下四轮转向车辆与前轮转向车辆稳态侧向加速度之差较大，即速度越高，四轮转向车辆的操纵稳定性优势越明显。

图11 侧向加速度阶跃响应比较Fig.11 Comparison of lateral acceleration step response

5 结语

在四轮转向提出初期，主要的控制方式为保证车辆的质心侧偏角为0[14]，这样在转向时车辆会有更好的循迹性，并提高低速转向时的灵活性和高速转向时的操纵稳定性。本文根据方程式赛车设计的后转向梯形经过优化，用角阶跃输入响应分析，证明了该后轮转向梯形和前转向梯形匹配，并提高了赛车的操纵稳定性。

[1]伍颖，宋康顿，吴选杰，等.循环球式转向器磨损试验助力泵站的设计与实现[J].机床与液压，2015，43（14）：75-77．

[2]李晏，王瑾，谭修文，等.汽车转向器齿轮齿条的建模与仿真研究[J].现代制造工程，2010（12）：73-76．

[3]王望予.汽车设计[M].北京：机械工业出版社，2004．

[4]任延，杨家军，刘照.电动助力转向器硬件在环仿真系统的设计[J].湖北工学院学报，2004，19（3）：44-46．

[5]日本自动车技术会.汽车工程手册[M].北京：北京理工大学出版社，2010．

[6]李理光.2016中国大学生方程式汽车大赛规则[M].中国汽车工程学会，2016．

[7]柴天.FSAE赛车整车性能分析与研究[D].湖南：湖南大学，2009．

[8]程勇.四轮转向商用车前后转向梯形优化设计[D].湖北：武汉理工大学，2014．

[9]刘战芳.4ws车辆的建模和控制方法的研究分析[D].安徽：合肥工业大学，2008．

[10]颜四平，黄玲琴，周淑文.基于ADAMS的四轮转向汽车虚拟样机建模与动力学仿真[J].汽车科技，2007（5）：14-17．

[11]RongrongWang，HuiZhang，Junmin Wang.Linearparametervarying controller design for four-wheel independently actuated electric ground vehicles with active steering systems[J].Control System Technology，2014，22（4）：1283-1295．

[12]杨叔子，杨克冲.机械工程控制基础[M].6版.武汉：华中科技大学出版社，2011．

[13]舒进，陈思忠.四轮转向车辆运动计算分析[J].湖北汽车工业学院学报，2002，16（3）：1-5．

[14]Sano S，Furukawa Y，Shlralshis.Fourwheel steering system with rear wheel steer angle controlled as a function of steering wheel angle[J].SAEPaper860625，1986.