一道高中联赛题的解法赏析与推广*

●

(汤池中学,安徽 岳西 246620)

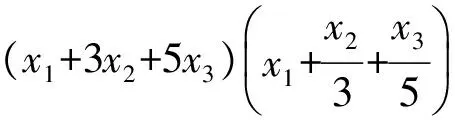
(2017年全国高中数学联赛试题第10题)

本题形式简单，结构优美，背景公平，主要考查三元柯西不等式、均值不等式的基础知识，考查学生的算式变形能力、运算能力、分析和解决问题能力等，对学生的逻辑推理能力要求较高，是一道难度适中的好题，在解题过程中，能够展示学生的代数整合意识.

1 解法赏析

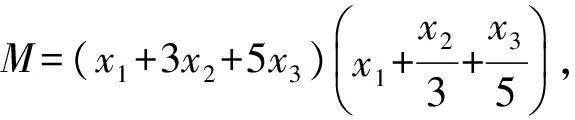
当x1=1,x2=0,x3=0时不等式取等号，故M的最小值为1.

又由基本不等式可得

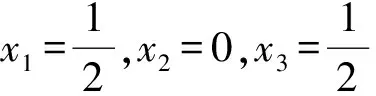
评注“抓基础，重转化”是学好中学数学的基础，转化的作用有熟悉化、简单化、直观化等.本解法抓住了柯西不等式的结构化特征，比较容易求出了最小值，学生易想易解，在求最大值时抓住均值不等式的结构特征“和为定值积最大”，剩下的问题就是配系数使和为定值.

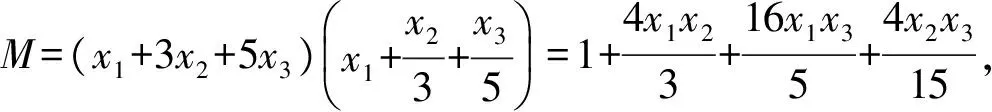
又因为x1+x2+x3=1,当x1=1,x2=0,x3=0时不等式取等号，故M的最小值为1.又由基本不等式可得

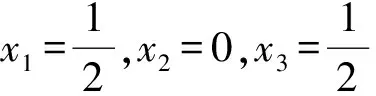
评注本解法需要善于观察，对配方的要求较高.

解法3求最小值同解法1或者解法2.下面求最大值：由基本不等式可得

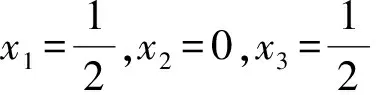
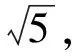
解法4求最小值同解法1或者解法2.求最大值先给出一个推广：若x1,x2,x3是非负实数，满足x1+x2+x3=1，且0<λ1<λ2<λ3，则

(1)

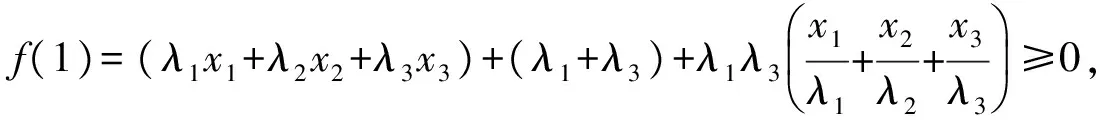
从而函数f(x)在(-1,1)上必存在零点，于是

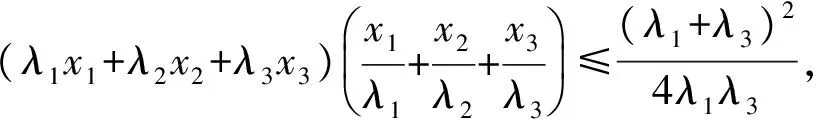
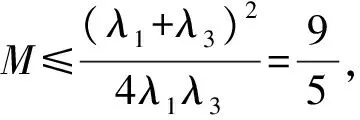
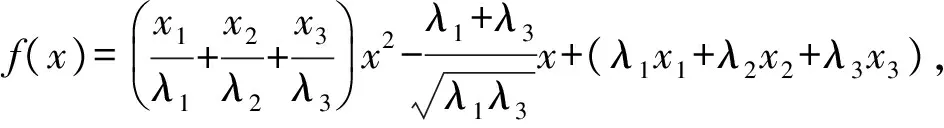
2 类比推广

本题可以作如下推广：

推广1若x1,x2,x3是非负实数，满足x1+x2+x3=1，且0<λ1<λ2<λ3，则

推广2若x1,x2,x3,…,xn是非负实数，满足x1+x2+…+xn=1，则

当n=3时，推广2即为2017年全国高中数学联赛试题第10题.

推广3[1]若x1,x2,x3,…,xn是非负实数，满足x1+x2+…+xn=1,且0<λ1<λ2<…<λn,则

推广4若x1,x2,x3,…,xn是非负实数，满足x1+x2+…+xn=a，且a>0,0<λ1<λ2<…<λn，则

下面给出推广4的证明:

证明由柯西不等式可得

(x1+x2+…+xn)2=a2.

由基本不等式可得

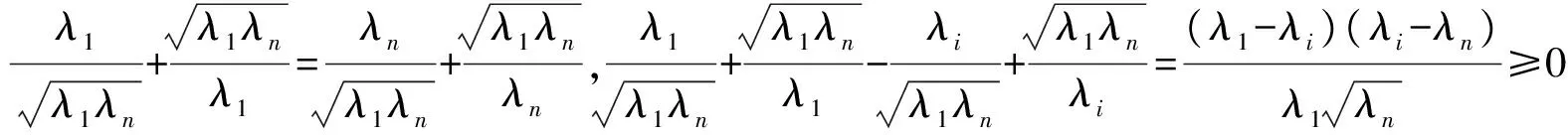
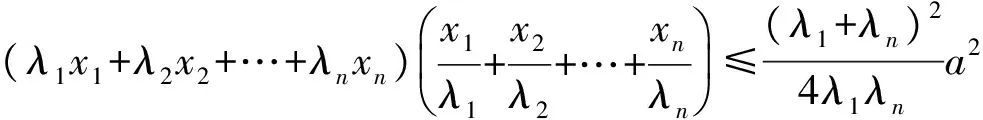
一道好题的平淡之中见深刻的命题意图和考查目的，根植于基础知识和基本方法的考查.本题是以柯西不等式、均值不等式、二次函数、二次方程为解题的落脚点，作为竞赛题真正体现了《全日制普通高级中学数学教学大纲》中所规定的教学要求和内容，但在方法的要求上有所提高.同时，也注重考查基本知识和基本技能的掌握情况和综合、灵活运用知识的能力，试题的命制遵循通性通法的解题原则：思想越自然越好、方法越简单越好、所用知识越简单越好.

[1] 吴振奎．Канторович不等式又一初等证明[J]．中等数学，1998(1)：21．