数形结合思想方法*
2018-01-17
●
(萧山中学,浙江 杭州 311201)
1 考点回顾
数形结合作为重要的数学思想方法,历来是高考考查的重点内容.许多数学问题只有从“数”与“形”两个角度去理解才能更好地把握其数学本质.运用数形结合思想解题时,既要分析其代数意义,又要揭示其几何直观,使数量关系的精确刻划与空间形式的直观形象巧妙、和谐地结合在一起,这样才能使问题化难为易、化繁为简.
数形结合解题操作包括“以形助数”和“以数辅形”两个方面:一是借助形的生动和直观性来阐明数之间的联系;二是借助于数的精确性和规范严密性来阐明形的某些属性.在运用“以形助数”时,需要深谙某些特定的代数结构所对应的图形意义,并熟练掌握常见图形的画法及图形变换过程;在运用“以数辅形”时,需要正确转化图形与符号两种语言,并具备较强的运算求解、逻辑思维、综合运用等能力.
2 典题剖析
2.1 以形助数
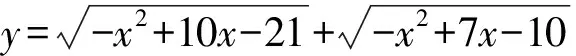
分析将函数解析式化为
y=a·b=|a|·|b|·cos


图1
评注如果根号内部二次函数能够配方,那么可以将根式看作两点间距离来观察值域.本题别出新裁,利用向量数量积来转化问题.

( )
A.{Sn}为递增数列 B.{Sn}为递减数列
C.{S2n-1}为递增数列,{S2n}为递减数列
D.{S2n-1}为递减数列,{S2n}为递增数列

……
不难得到
bn+cn=2a1.
而BnCn长为定值a1,若固定三角形的两顶点Bn,Cn,则顶点An在以Bn,Cn为两焦点的椭圆上运动.又因为
所以点An在椭圆短轴两侧摆动并逐步趋近于短轴顶点(如图2),故选A.

图2
评注本题中面积Sn的数量并不需要求出,关键在于利用△AnBnCn三边长满足的特定关系,结合椭圆定义,通过观察图形便能直接解决.
小结以形助数解题的关键是揭示代数式表达的几何图形含义,比如一次函数式的系数代表直线的斜率和截距,构造函数并利用函数单调性解不等式等.
2.2 以数辅形
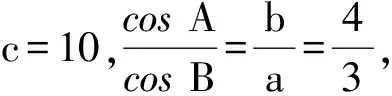
分析由正弦定理易知C=90°,a=6,b=8.分别以CB,CA所在直线为x轴和y轴建立直角坐标系(如图3),则C(0,0),B(6,0),A(0,8),内切圆方程为
(x-2)2+(y-2)2=4.
可设点P的坐标为(2+2cosA,2+2sinA),则
|PA|2+|PB|2+|PC|2=80-8sinA≤88,
即点P到顶点A,B,C的距离平方和的最大值为88.
评注解析法是典型的以数辅形的方法,通过建立直角坐标系,用坐标表示点,用方程表示曲线,从而将几何问题转化为代数问题.

图3 图4
例4在棱长为4的正方体ABCD-A1B1C1D1中,M是正方形BB1C1C的中心,P是△A1C1D内(包括边界)的动点,满足PM=PD,则点P轨迹的长度等于______.
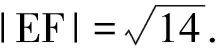
评注在空间直角坐标系中,要求出线段的长度,只需求出线段的两个端点的坐标.在立体几何中,用坐标法来解决几何问题也充分体现了以数辅形的方法.
例5在四面体P-ABC中,已知PA⊥BC,PB⊥AC,求证:PC⊥AB.

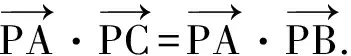




故
PC⊥AB.
评注向量兼具几何特性和代数特性,引入向量来解决几何问题也体现了以数辅形的方法,坐标法的实质是向量法的特殊情形(当向量用单位正交基表示时).
小结运用代数方法不仅可对图形作出定性分析(如平行、垂直等),也能对图形进一步作定量计算(如长度、角度、定值、最值等).
2.3 数形互助


图5

评注先将函数问题化为图形问题,再用代数计算分析图形关系,而在(-∞,-2)内有一个零点又可用指数增长的特性来直观判断.



图6
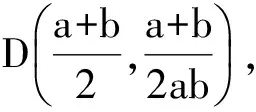
从而
即
kOD=-kEF,
同理可得
kOE=-kDF,
于是
∠DOE+∠DFE=π,
因此原点O在△DEF的外接圆上.
评注先利用图形的对称性给出猜想,再对猜想的结果进行证明,常需要用解析法(代数化),而运用代数运算结果作判断时又要用到代数结果所反映的图形特征.
小结利用数形结合思想方法解题时,需不断根据图形观察来确定代数运算思路(以形助数)、用代数运算结果分析图形的细节特征(以数辅形),由此在数与形的反复转化中解决问题.当然,对图形的变化规律需要有正确的把握,否则会被图形误导,产生错误(如例6,不少学生误认为只有两个零点).
3 精题集萃
1.到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是
( )
A.直线 B.椭圆 C.抛物线 D.双曲线

( )

图7
3.如图7,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折.若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是
( )

4.在等差数列{an}中,a1∈[0,1],a2∈[1,2],a3∈[2,3],则a4的取值范围为
( )

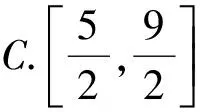

8.正△ABC顶点A在平面α内,顶点B,C在α外同一侧,D为BC的中点.若△ABC在α上的投影是以A为直角顶点的三角形,求出直线AD与平面α所成角的正弦值的范围.
9.已知过点A(0,1)和B(4,a)(其中a≠0)且与x轴相切的圆只有一个,求该圆的方程.
参考答案
1.D 2.D 3.A 4.C
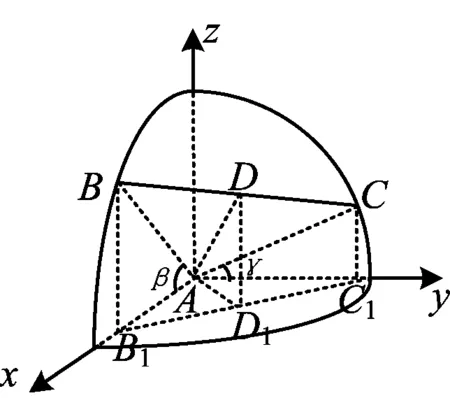
图8

因此
从而
故
9.解设圆心C(m,n),因为圆与x轴相切,所以半径r=|n|.又因为圆过点A(0,1)和B(4,a),所以
r2=n2=m2+(n-1)2=(m-4)2+(n-a)2,
整理得
将式(1)代入式(2),消去m,得
(1-a)m2-8m+16-a+a2=0.
因为符合条件的圆只有一个,所以上述关于m的方程只有一个解,可得

解得
a=1或a=0(舍去),
故
从而圆的方程为
