同课异构显风采 题组变式来复习*——对新一轮高考复习课的几点思考

●

(衢州第二中学,浙江 衢州 324000)

1 教学案例1

1.1 知识梳理

教师直接切入正题，和学生一起从概念复习入手，回顾了“基本不等式”这节内容主要涉及的3个问题：

1)重要不等式：若a,b∈R，则a2+b2≥2ab，当且仅当a=b时等号成立；

3)应用不等式求最值注意的3个重要条件：一正、二定、三相等.

1.2 正本清源

接下去教师马上通过PPT展示以下一个题组，然后让学生开始辨析正误.

2)已知x≥0，那么f(x)=1+x2≥2x≥0；

点评教师通过以上题组3个问题的辨析，恰好从“一正、二定、三相等”3个方面对基本不等式求最值的3个条件进行了逐一验证.由于题组3个问题的设置较为简单，学生基本都能解决，这样既复习了内容，也再次强调了3个条件缺一不可.

1.3 应用举例

在接下来的教学过程中，教师先是以例1的形式改编了书本上一个简单的练习题.之后教师进行了一系列的变式教学.

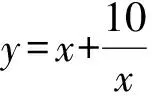
(人教A版《数学(必修5)》第100页练习1改编)

点评教师先对教材上习题进行简单的改编，然后进行一系列的变式拓展，在难度上有一个由易到难的梯度，这样既能照顾到不同层次的学生，使所有学生都能参与进来，又能让他们体会到题目之间的变迁联系，可以更好地理解和掌握知识.

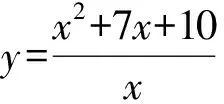
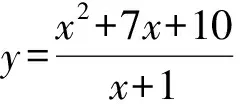
点评教师通过变式2和变式3，强调当基本不等式不能直接使用时，可以做适当变形，使得基本不等式派上用场.通常也可以用换元法，如变式3中可以令t=x+1，但应注意的是换元以后新变量的范围有限制，通过换元可以将问题化归为形如变式1的问题.变式4也可以通分化归到变式3，进而化到变式1.

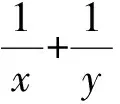
这样就转化为变式4的情形了(略).

解法2(1的代换)

教师最后强调解法2同样适用在变式4中，只要将1看成是(1-2x)+2·x即可，由于时间关系就留给学生课后思考.

点评笔者认为案例1中教师这样的题组安排与变式设计是比较合理的,其中设置的两个题组都是围绕着教学目标和重点展开的.尤其是例1问题的引入是从教材上一个简单的习题开始，然后经过4个变式题螺旋式呈现，符合学生的认知规律，逐步深入，让学生体会到题目的演变规律，在变中发现不变的本质.通过例2的呈现，将问题的难度以及解法的广度又往前推了一步，使整堂课达到一个高潮.

2 教学案例2

2.1 复习定位

教师在教学内容的引入上先是用PPT展示了《考试说明》上的要求：会用基本不等式解决简单的最大(小)值问题，为本节课的复习奠定了基调.之后教师与学生一起回顾了“基本不等式”的内容及常用的3个变形：

1)a2+b2≥2ab;

2.2 小试牛刀

教师通过一个简单的题组让学生思考并弄清基本不等式求最值应满足的3个基本条件：一正、二定、三相等.

3)已知a>0,b>0，且a+b=1，求ab的最大值；

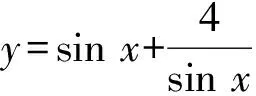
2.3 走向高考

纵观近几年的浙江省数学高考，不等式题型以“已知两个变量的一个等量关系求最值问题”出现的频率较多.

例4已知x>0，y>0，且3x+y=1，求3x·y的最大值.

变式1已知x>0，y>0，且3x+y=1，求2x·(x+y)的最大值.

教师从例4这个简单问题入手，学生可直接根据“和为定值，积有最大值”的结论进行判断.变式1和变式2也可以通过“不等式串”快速找到目标式与已知条件之间的关系，求出最大值即可，当然过程中还要注意到等号取到的条件.

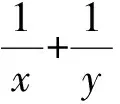
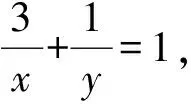
教师通过变式3和变式4，说明当目标式和已知条件间关系难建立时，可以考虑将“1”作“3x+y”的代换，这样就能构造出积为定值的情况.与变式4类似，只要把分式转成整式，即可得变式5和变式6，从而让学生体会高考题的改编历程.

变式5已知x>0，y>0,且3x+y=xy，求x+y的最小值.

变式6已知x>0，y>0，且x+3y=5xy，求3x+4y的最小值.

(2012年浙江省数学高考文科试题第9题)

通过以上两个变式题，学生可以感受到高考题并不神秘，并且从中找到了成功的喜悦.教师借此又增加了一个常数6，继续改编得到变式7.

变式7已知x>0，y>0，且2x+y+6=xy，求xy的最小值.

(2010年浙江省数学高考文科试题第15题)

点评案例2中教师关于本节复习课的设计是别具一格的.整堂课紧紧围绕着“已知二元变量的等量关系求解最值问题”展开，通过例4得到7个变式，问题的设计由易到难，精心巧妙，体现了问题循序渐进的过程，最后改编还得到了2010年和2012年的高考真题.从课堂气氛来看，达到了较好的复习效果.

3 对新一轮高考复习课的思考

高三数学复习课作为整个高中数学课堂教学的重中之重，如何进行高效复习成了每位教师最关注的话题.笔者发现，教师的行动非常重要，除了要清楚高考考什么(即明确复习课的定位)以外，对复习课的选题、组织形式、数学思想方法的渗透等方面也应充分考虑，只有这样才能使学生少走弯路.以下是笔者结合此次同课异构课，对于复习高效性的几点思考：

3.1 复习课的选题要精益求精

教师在知道了高考考什么以后，要考虑的问题就是怎么考.一节课堂40分钟，可能讲解1～2个综合性强点的高考题或是模拟题就已经不够用了.如何才能提高效率？笔者认为选题是至关重要的.既然不可能面面俱到，那选题就应精益求精，选一些具有典型性、代表性的例题.那么该从何处来选题呢？笔者认为有两个很好的题源值得每位教师研究：一是教材上的一些例题或习题，这些题目还是有相当丰富的内涵和广阔的外延的，合理地挖掘，可以提升其价值；二是高考真题，高考真题应是出卷人智慧的集中体现，适度地拓展加深，也可以展现数学独特的魅力.

从这一点看，案例中的两位教师对于复习课的选题还是动过一番心思的：案例1的教师选择从教材上最基本的不等式求最值入手，题目入口较宽，然后适当变式，使班中不同层次的学生都能有收获；而案例2的教师把目标定在了高考真题上，为了降低难度让每位学生可以跳一跳够得到，该教师采用递进式教学，层层铺垫最终把学生带进高考，展示近几年浙江省数学高考卷中不等式题的变迁过程，破解出高考题的本质，相信每个学生都应是有收获的.

3.2 题组与变式要精心设计

复习课的高效同样离不开课堂的组织形式.笔者认为在复习课中恰当地开展题组与变式可以大大提高复习的有效性.题组中的题目由易到难，由单一到综合，使基本知识、基本技能、基本数学思想方法在题组中反复出现.这样不仅可以强化学生的认识，还可以帮助教师了解学生的掌握情况.

笔者认为上述两个案例教学之所以取得较好的成效，与两位教师在题组与变式教学上下功夫有很大关系.数学教学的主要任务是培养学生的思维能力，然而很多时候学生并不会去想“为什么可以这样做，而不能那么做”，通过题组与变式的过程可以将学生的思维逐步引入到更高的层次.当然，教师对于题组与变式要精心设计，不能为“变式”而变式，使变式成为一种形式.不恰当的变式只是一种生搬硬套，揭示不了题目间的内在联系.

在案例2中，教师对题组中的问题进行了精心设计，并由例4演变出了7个变式题，这些变式层层递进，虽然只有两个题组，但蕴含的题量，涉及的数学内容和思想方法却是相当饱满丰富的.这样的设计使学生可以在题组与变式下辩证地思考问题，可以从中体会到题目之间的变迁关系，而这样的变迁可能就可以深挖出高考出题的源头,让学生觉得高考并不那么神秘.

波利亚说过：“一个专心备课的教师能够拿出一个有意义但又不会太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的理论领域.”因此适当地变式教学可以真正地以点带面，提高复习的有效性.

3.3 数学思想要与解题方法并进

数学思想是数学解题的依据，在数学教学的过程中不可或缺.但事实上很多教师在复习课中太过于关注解题方法，以至忽视了数学思想的渗透.从这点看，两位教师在概念复习时都有欠缺，即将教学局限在几个重要结论的回忆上.

本节课涉及的数学思想，首先应是转化化归思想，当基本不等式不能使用时，像案例1中的例2及案例2中的例4及7个变式都可以用消元这样一种通性通法去解决，同时这样还可以体现函数不等式的思想.如果再继续考虑，那么还可以引出线性规划问题，体现数形结合思想.笔者建议最后思想方法的小结应交给学生，教师可以引导但不是蜻蜓点水般地灌输给学生.

事实上，如何更好地提高课堂效率是一个永久的话题，没有固定的方法，我们唯有不断地实践探究，相互切磋，试着从教学实际中找到我们永恒追求的方向.