例谈在高三课堂激发学生创新思维*——一道数列试题的探究性教学

●

(曲靖市第一中学,云南 曲靖 655000)

创新是新课标改革后高考试题最显著的特征，传统的题海战术已很难让学生在高考中赢得高分，无论高考如何改革，考查学生解题的创新思维不会改变.教育家第斯多惠说过：“一个坏教师奉送给学生真理，一个好教师则教学生发现真理.”很多教师都在探索如何在课堂中激发学生解题的创新思维[1]，笔者认为，学生创造性思维的培养从改变课堂开始.

下面是笔者的一堂试题讲评课.如下例1的答题情况很不理想，方法单一，笔者以此题为突破口，转变以往的试题讲评方式，将“教师讲解、学生理解”变为“教师引导、学生展示”.学生通过思考找到一种又一种解答方式的同时，内心获得满满的成就感，从而带动课堂氛围逐步热烈.通过这堂课，学生不仅明白了创新思维的含义，还建立了对数学学习的信心.

例1在数列{an}中，a1=2，若平面向量bn=(2,n+1)，cn=(-1+an+1-an,an)平行，则{an}的通项公式为______.

(2017年云南省第二次数学统测理科试题第16题)

解法1先根据向量bn∥cn，可化简得

(1)

…

从而猜想

证明略.

评注根据填空题的特征，学生在考场上普遍选用了归纳推理的解题方法，但规律难寻，得出正确结果的学生很少.于是教师引导学生根据曾经讲过的数列求通项的模型：an+1=kan+λ及an+1=kan+f(n)，逐步打开学生思考的空间.

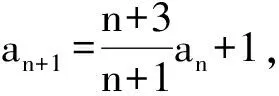
化简得

从而

即

An+2B-A=n+1,

得

A=1,B=1，

故

解法3根据式(1)可得方程组

两式相减,得

化简得

bn+bn+2=2bn+1,

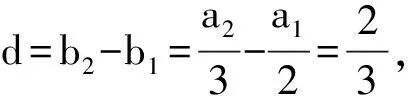
故

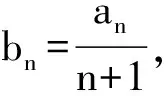
式(1)可化为(n+2)bn+1=(n+3)bn+1,两边同除以(n+2)(n+3),得

于是

故

解法5[2](迭代法)由式(1)知

…

教师在学生展示解题方法的同时，不断提示学生注意解题方法中的共性，学生在热烈探讨中归纳总结出解决此类题型的通用方法，整理如下：

1)迭代法可作为此类题型的通用方法[2]，但是计算较麻烦.

两式相减,得

分子中代入t2=t1-2k,得

化简得

故

bn+bn+2=2bn+1,

从而数列{bn}为等差数列.令bn=Mn+N,则

an=(kn+t2)(Mn+N),

于是数列{an}的通项公式是n的二次函数式.

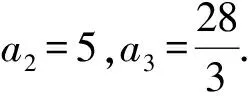
高考试题中总有部分试题会让考生感觉既熟悉又陌生，怎样才能在有限的时间内找到合适的解法呢？唯有创新.创新是指发现新事物、提出新见解、揭示新规律、创造新方法、建立新理论、解决新问题等思维过程.但笔者认为:高中生创新更应注重过程，步子不必迈得过大，创新并不是无中生有，就像例1，用熟悉模型的构造方法去建构我们不熟悉模型的解题思路，就是创新思维，它如同老树开新芽，一点一点来长大，新芽变老枝，老枝再开花.创新，从现在开始，从我们做的每一道题开始.

笔者在这堂课的最后发现每一个参与进来的学生都很兴奋，与以往教师用多种方法讲题的课堂氛围完全不一样.学生进入高三，他们的认知基础、思维方式、计算能力、探究能力较高一、高二都有大幅度提升，大多数学生都期盼做数学学习的“真正主人”.在课堂中，教师的合理放手、适度让位，让他们体验到了创新和成功的快乐，这种体验为学生的探究创新注入了强大的精神动力[3].将课堂还给学生，相信学生的创造性是无限的，教师在教学过程中要做有心人，及时抓住典型问题，点燃学生的思维之火，如此，师生定能合作出一节节精彩的课堂.

[1] 邱友会,李德安.一节培养创新能力的数学课[J].中学教研(数学),2016(3)：11-14.

[2] 陈立斌,陈秀娥.对一道2011年数学联赛数列题的探究及思考——兼谈递推数列问题的解题策略[J].中国数学教育:高中版,2012(4)：46-48.

[3] 郎建林.裂项法求和问题的生成方法及其作用[J].中学教研(数学),2017(5)：16-18.