线性变换张量积的Jordan-Chevalley分解
2018-01-16,,
,,
(上海理工大学 理学院,上海 200093)
1 张量积的基本性质
在李理论中,Jordan-Chevally分解指出任意一个线性变换可唯一地表示成它的可交换的半单部分和幂零部分的和[1].文献[2] 指出该分解存在当且仅当所讨论的基域完备.线性变换张量积在数学、物理等领域中有着广泛的应用,而2个线性变换张量积的Jordan-Chevalley分解理论目前国内外研究还比较少,本文将在代数闭域上探讨2个线性变换张量积的Jordan-Chevalley分解,首先通过矩阵表示讨论2个线性变换张量积的一些基本性质,接着证明该张量积的Jordan-Chevalley分解的唯一存在性,并利用这些结论给出具体表达式.
定义1[3]设是代数闭域,V,W是域上的有限维向量空间,且dimV=m,dimW=n.∀x0∈V,y0∈W都有唯一的积z=x0⊗y0与之对应,并且对于固定y0,x0与z的对应是线性的; 对于固定x0,y0与z的对应是线性的.这种对应关系称为V与W的张量积,记为V⊗W,它构成一个向量空间.
性质1[3]∀x0,x1,x2∈V,y0,y1,y2∈W,a∈,
a.0⊗y0=x0⊗0=0;
b.(ax0)⊗y0=x0⊗(ay0)=a(x0⊗y0);
c.(x1+x2)⊗y0=(x1⊗y)+(x2⊗y0);
d.x0⊗(y1+y2)=(x0⊗y1)+(x0⊗y2).
性质2[3]设BⅠ:{v1,…,vm}为V的一组基,BⅡ:{w1,…,wn}为W的一组基,则BⅢ:{vi⊗wj:i=1,…,m;j=1,…,n}为V⊗W的一组基,且dim (V⊗W)=mn.
性质3[4](张量积的普遍性质) 设φ:V×W→V⊗W是一个双线性映射,对任意给定的向量空间Z,若存在一个双线性映射h:V×W→Z,那么,存在唯一的线性映射h′:V×W→Z使图1可交换,即h=h′∘φ.

图1 交换图Fig.1 Commutative diagram
2 End (V⊗W)及其矩阵表示
定义2如果线性变换x的极小多项式无重根,称x是半单的.如果讨论的基域是代数闭域,等价于该线性变换的矩阵可对角化.
定义3如果存在正整数k,使得xk=0,那么,称线性变换x幂零.
式中,δsk为Kronecker函数.
定理1EndV⊗EndW≅End (V⊗W)
证明对∀x∈EndV,y∈EndW,定义映射Tx,y:V⊗W→V⊗W,满足
Tx,y(v⊗w)=x(v)⊗x(w),∀v∈V,w∈W
由张量积的性质易验证Tx,y是线性的,即Tx,y∈End (V⊗W).再令
φ:EndV×EndW→EndV⊗EndW,
φ(x,y)=x⊗y
h:EndV×EndW→End (V⊗W),
h(x,y)=Tx,y
显然,φ,h是双线性的.由性质3可知,存在唯一的线性映射h′:EndV⊗EndW→End (V⊗W),使得h=h′∘φ.再取EndV的一组自然基eis:1≤i,s≤m,EndW的一组自然基fjt,1≤j,t≤n,根据性质2,EndV⊗EndW有基eis⊗ftj,且
这说明{Teis,fjt|1≤i,s≤m,1≤j,t≤n}构成End (V⊗W)的一组自然基,h′将EndV⊗EndW的基向量eis⊗ftj映到End (V⊗W)的基向量Teis,fjt,故h′是同构映射,定理1得证.
由定理1可知,可以将EndV⊗EndW中的元与End (V⊗W)中的元等同起来,即∀z∈End (V⊗W),存在x∈EndV,y∈EndW,使得z=x⊗y且(x⊗y)(v⊗w)=x(v)⊗y(w).
引理1[5]若x∈EndV在基BⅠ下的矩阵为A,y∈EndW在基BⅡ下的矩阵为B,则x⊗y在基BⅢ下的矩阵为A⊗B,即A与B的Kronecker积.具体地,若A=[aij]m×n,B=[bij]p×q矩阵,则
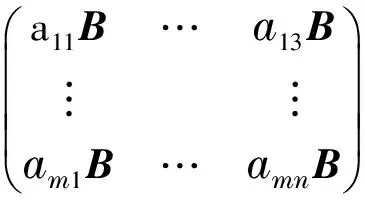
现探讨A⊗B的一些相关性质,根据线性变换与矩阵的一一对应关系,x⊗y有对应的性质4~8.
性质4[5]a.(A⊗B)(C⊗D)=(AC)(BD); b.A⊗B可逆当且仅当A,B可逆,且(A⊗B)-1=A-1⊗B-1.
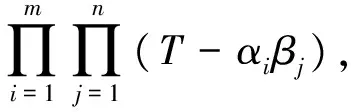
性质6若A和B都是可对角化的矩阵,则A⊗B也可对角化.
证明因为,A,B可对角化,则存在可逆的矩阵P和Q,使得P-1AP=Λ1,Q-1BQ=Λ2,其中,Λ1,Λ2是对角矩阵,由性质4可得
所以,
(P⊗Q)-1(A⊗B)(P⊗Q)=Λ1⊗Λ2
显然,Λ1⊗Λ2仍是对角矩阵.
性质7[7-8]A⊗B幂零当且仅当A和B中至少一个幂零.
证明一个矩阵幂零当且仅当它的所有特征值为0.现设α1,…,αm是矩阵A的所有特征值,β1,…,βn是矩阵B的所有特征值,由性质5可知,A⊗B的特征值为{αiβj:1≤i≤m;1≤j≤n} .
充分性:若A,B中至少一个幂零,那么,所有的α1,…,αm为0,或者,所有的β1,…,βn为0,这使得的所有A⊗B特征值都为0,从而A⊗B幂零.
必要性:若A⊗B幂零,但A和B都不幂零,则一定存在某个αi和βj都不为0,从而αiβj不为0,这与A⊗B是幂零的条件矛盾.
性质8若矩阵A与C可交换,矩阵B与D可交换,则A⊗B与C⊗D可交换.
证明若AC=CA,BD=DB,则(A⊗B)(C⊗D)=(AC)(BD)=(CA)(DB)=(C⊗D)(A⊗B).
3 x⊗y的Jordan-Chevalley分解
定理2设V,W是代数闭域上的2个有限维向量空间,则∀x⊗y∈End (V⊗W)有唯一的Jordan-Chevalley分解:x⊗y=(x⊗y)s+(x⊗y)n,其中,(x⊗y)s是半单部分,(x⊗y)n是幂零部分,且(x⊗y)s和(x⊗y)n可交换.
证明设α1,…,αk是x的互不相同的特征值,重数为m1,…,mk;β1,…,βs是y的互不相同的特征值,重数为n1,…,ns.由性质5可知,x⊗y有特征多项式
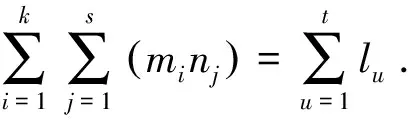

p(T)≡λu(mod (T-λu)lu)
p(T)≡0(modT)
设q(T)=T-p(T),显然,p(T),q(T)是关于T的常数项为0的多项式.令
(x⊗y)s=p(x⊗y),(x⊗y)n=q(x⊗y)
则x⊗y,(x⊗y)s和(x⊗y)n可两两交换.对∀u,p(T)≡λu(mod(T-λu)lu)意味着(x⊗y-λuidV⊗W)限制作用到(V⊗W)u为零变换,因此,(x⊗y)s对角地作用在(V⊗W)u上,其特征值只有λu.又(x⊗y)n=(x⊗y)-(x⊗y)s,显然,(x⊗y)n是幂零的.现证唯一性[7],若x⊗y还存在另一个Jordan-Chevalley分解x⊗y=s+n,s半单,n幂零,且sn=ns,则有(x⊗y)s-s=n-(x⊗y)n,又因为可交换的半单或者幂零的线性变换和还是半单或者幂零的,因此,(x⊗y)s-s=n-(x⊗y)n既半单又幂零,只可能为0,因此,s=(x⊗y)s,n=(x⊗y)n.
定理3若x的Jordan-Chevalley分解为x=xs+xn,y的Jordan-Chevalley分解为y=ys+yn,那么,x⊗y的Jordan-Chevalley分解的半单部分是xs⊗ys,幂零部分是xs⊗yn+xn⊗ys+xn⊗yn.
证明因为,x⊗y=(xs+xn)⊗(ys+yn)=xs⊗ys+xs⊗yn+xn⊗ys+xn⊗yn,由性质6可知,xs⊗ys是半单的,由性质7可知,xs⊗yn、xn⊗ys,xn⊗yn是幂零的,由性质6可知,xs⊗ys,xs⊗yn,xn⊗ys和xn⊗yn是两两可交换的,所以,它们的和xs⊗yn+xn⊗ys+xn⊗yn还是幂零的,且与xs⊗ys可交换.由Jordan-Chevalley分解的唯一性可得
(x⊗y)s=xs⊗ys
(x⊗y)n=xs⊗yn+xn⊗ys+xn⊗yn
由定理3可知,对任意给定的正整数k,可得
(x⊗y)k=xk⊗yk=(xs+xn)k⊗
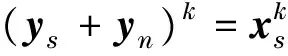

[1] HUMPHREYS J E.Introduction to Lie algebras and representation theory[M].New York:Springer-Verlag,1972.
[2] BOURBAKI N.Lie groups and Lie algebras[M].Berlin:Springer,2008.
[3] 林杰,林新棋.线性变换的张量积[J].福建广播电视大学学报,1998(2):37-40.
[4] ROTMAN J J.An introduction to homological algebra[M].New York:Academic Press,1960.
[5] DUMMIT D S,FOOTE R M.Abstract algebra[M].Hoboken:John Wiley and Sons,2004.
[6] GLASBY S P.On the tensor product of polynomials over a ring[J].Journal of the Australian Mathematical Society,2001,71(3):307-324.
[7] 闫爱民,胡建华.型E7根系的结构[J].上海理工大学学报,2014.36(1):5-11.
[8] 胡建华,赵卫萍.一类特殊幂零李代数的结构[J].上海理工大学学报,2015.37(3):215-219.
