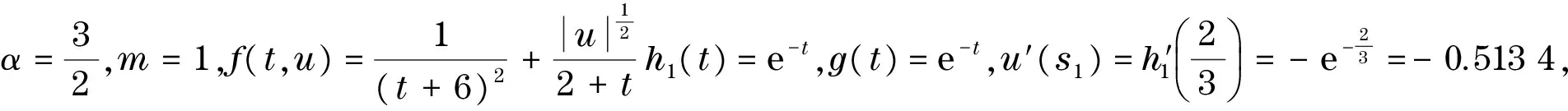一类具有非瞬时脉冲的分数阶微分方程积分边值问题解的存在性
2018-01-16,,
, ,
(上海理工大学 理学院,上海 200093)
1 问题的提出
近年来,分数阶微分方程在现代科学技术领域的应用日益广泛,其理论研究也取得了巨大的进展[1-8].作为刻画突变现象的脉冲微分方程在电子技术及通讯工程等方面发挥了巨大的作用,瞬时脉冲理论也受到人们的关注[9-13].在生物技术及医药工程领域存在着大量的非瞬时脉冲现象[14-20],对这类现象进行研究具有重要意义.本文研究一类具有非瞬时脉冲的分数阶微分方程积分边值问题
(1)
定义空间:PC(J,):={u:J→存在,且取范数‖u‖PC=则PC(J,)为Banach空间.
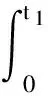
H0g∈L1(J),且ρ≠0.
2 预备知识与引理
有关分数阶微积分的定义可参见文献[1-4].
定义1设u∈PC(J,),若u满足边值问题(1)中的各等式,则称u是边值问题(1)的一个解.
引理1[4]假设y∈L[0,1],且1<α<2,那么,Cauchy问题
(2)
有解,且以下列形式给出:

推论1假设y∈L[0,1],且1<α<2,那么,Cauchy问题
(3)
存在唯一解
引理2对任意的y∈L1[0,1],且H0成立,则边值问题
(4)
存在唯一解
u(t) =v(t)+G(t)
(5)
其中
(6)
(7)

(8)
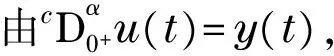
根据边界条件u(0)=0,可得c0=0,故
(9)

考虑 Cauchy问题
(10)

类似地,当t∈(sk,tk+1],k=1,2,…,m时,
因此,
另一方面,
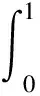
将上式代入式(9),可得式(5)成立,即引理2得证.
经过化简与计算,易得下面的引理3和引理4.
引理3对任意的s∈J,有以下不等式成立:

为了方便起见,记
根据式(7),容易证明引理4成立.
引理4对任意的t∈J,不等式|G(t)|≤N2成立.
定义算子A:PC(J,)→PC(J,).
(11)
记
Tu(t) =Au(t)+G(t)
(12)
引理5若假设H0成立,则算子T:PC(J,)→PC(J,)全连续.
证明首先,证明T为连续算子.
设un,u∈PC(J,),n=1,2,…, 且‖un-u‖PC→0(n→), 即对任意的t∈J,有un(t)→u(t)(n→),由于f是连续函数,则|f(s,un(s))-f(s,u(s))|→0,n→.
故根据Lebesgue控制收敛定理,可得

因此,当t∈[0,t1]时,结合引理3的a,可得
当t∈(tk,sk],k=1,2,…,m时,|Tun(t)-Tu(t)|=0.
类似可得,当t∈(sk,tk+1],k=1,2,…,m时,
即有‖Tun-Tu‖PC→0(n→), 因此,T连续.
其次,证明T是紧的.
设B⊂PC(J,)为有界集,则存在r>0,使得对任意的u∈B,有‖u‖PC≤r,记则当t∈[0,t1]时,结合引理3的a与引理4,可得
当t∈(tk,sk],k=1,2,…,m时,|Tu(t)|=|hk(t)|≤Mh.
当t∈(sk,tk+1],k=1,2,…,m时,
因此,T(B)一致有界.


即T(B)等度连续.由Arzela-Ascoli定理可知T是紧的.
综合以上讨论,T是全连续算子.
3 边值问题解的存在性与唯一性
假设:
H1 存在非负函数a0,a1∈C[0,1], 常数σ>0, 使得对任意的t∈J及任意的x∈,有

H2 存在非负函数R∈C[0,1],使得对任意的t∈J及任意的x,y∈,有
|f(t,x)-f(t,y)|≤R(t)|x-y|
记‖a0‖‖R‖
定理1假设H0,H1成立,且0<σ<1, 则边值问题(1)至少存在1个解.
证明取r1≥max{Mh,2(N0‖a0‖
令D={u∈PC:‖u‖PC≤r1},则D为PC(J,)中非空有界闭凸集.
对任意的u∈D,当t∈[0,t1]时,结合引理3的b、引理4以及1<α<2,可得
当t∈(tk,sk],k=1,2,…,m时,|Tu(t)|=|hk(t)|≤Mh≤r1.
当t∈(sk,tk+1],k=1,2,…,m时,
因此,‖T‖PC≤r1, 故T(D)⊂D.由引理5可知T全连续,故由Schauder不动点定理可知T在D中至少存在1个不动点,即边值问题(1)在PC(J,)中至少存在1个解.
定理2假设H0,H1成立,如果σ=1,且0 当t∈(tk,sk],k=1,2,…,m时,|Tu(t)|=|hk(t)|≤Mh≤r2. 当t∈(sk,tk+1],k=1,2,…,m时, |Tu(t)|≤|Au(t)|+|G(t)|≤ N1‖a0‖+N2+r2N1‖a1‖≤r2 因此,‖T‖PC≤r2, 故T(D)⊂D.由引理5可知T全连续,故由Schauder不动点定理可知T在D中至少存在1个不动点,即边值问题(1)在PC(J,)中至少存在1个解. 定理3假设H0,H2成立,如果0 证明对任意的u1,u2∈PC(J,),当t∈[0,t1]时, 当t∈(tk,sk],k=1,2,…,m时,|Tu2(t)-Tu1(t)|=0. 当t∈(sk,tk+1],k=1,2,…,m时, 因为,0 考虑边值问题 (13) 综上可知定理1的所有条件均满足,根据定理1可知边值问题(13)至少存在1个解. [1] 白占兵.分数阶微分方程边值问题理论及应用[M].北京:中国科学技术出版社,2013. [2] 郑祖庥.分数微分方程的发展和应用[J].徐州师范大学学报(自然科学版),2008,26(2):1-10. [3] PODLUBNY I.Fractional differential equations[M].New York:Academic Press,1999. [4] KILBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and applications of fractional differential equations[M].Amsterdam:Elsevier,2006. [5] KOU C H,ZHOU H C,YAN Y.Existence of solutions of initial value problems for nonlinear fractional differential equations on the half-axis[J].Nonlinear Analysis:Theory,Methods & Applications,2011,74(17):5975-5986. [6] 李燕,刘锡平,李晓晨,等.具逐项分数阶导数的积分边值问题正解的存在性[J].上海理工大学学报,2016,38(6):511-516. [7] 刘帅,贾梅,秦小娜,等.带积分边值条件的分数阶微分方程解的存在性和唯一性[J].上海理工大学学报,2014,36(5):409-415. [8] 窦丽霞,刘锡平,金京福,等.分数阶积分微分方程多点边值问题解的存在性和唯一性[J].上海理工大学学报,2012,34(1):51-55. [9] 张莎,贾梅,李燕,等.分数阶脉冲微分方程三点边值问题解的存在性和唯一性[J].山东大学学报(理学版),2017,52(2):66-72. [10] WANG J R,LI X Z,WEI W.On the natural solution of an impulsive fractional differential equation of orderq(1,2)[J].Communications in Nonlinear Science and Numerical Simulation,2012,17(11):4384-4394. [11] LIU X P,JIA M.Existence of solutions for the integral boundary value problems of fractional order impulsive differential equations[J].Mathematical Methods in the Applied Sciences,2016,39(3):475-487. [14] HERNANDEZ E,O′REGAN D.On a new class of abstract impulsive differential equations[J].Proceedings of the American Mathematical Society,2013,141(5):1641-1649. [15] PIERRI M,O′REGAN D.ROLNIK V.Existence of solutions for semi-linear abstract differential equations with not instantaneous impulses[J].Applied Mathematics and Computation,2013,219(12):6743-6749. [16] GAUTA G R,DABAS J.Mild solutions for class of neutral fractional functional differential equations with not instantaneous impulses[J].Applied Mathematics and Computation,2015,259(15):480-489. [17] AGARWAL R,O′REGAN D,HRISTOVA S.Monotone iterative technique for the initial value problem for differential equations with non-instantaneous impulses[J].Applied Mathematics and Computation,2017,298(1):45-56. [18] WANG J R,ZHOU Y,LIN Z.On a new class of impulsive fractional differential equations[J].Applied Mathematics and Computation,2014,242(1):649-657. [19] LIN Z,WANG J,WEI W.Multipoint BVPs for generalized impulsive fractional differential equations[J].Computers and Mathematics with Applications, 2015, 258: 608-616. [20] WANG J R,ZHANG Y.A class of nonlinear differential equations with fractional integrable impulses[J].Communications in Nonlinear Science and Numerical Simulation, 2014, 19: 3001-3010.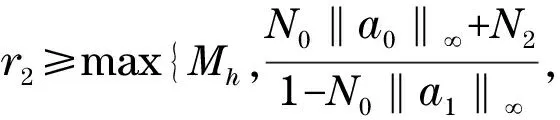
4 例 子