一类具有产毒浮游植物的扩散浮游生物模型的全局动力学行为
2018-01-16,,
,,
(1.上海理工大学 理学院,上海 200093; 2.江苏大学 理学院,镇江 212013)
1 问题的提出
近年来,淡水湖泊中蓝藻水华现象的频发不但影响了自然生态环境和淡水渔业生产,还严重威胁着人类的身体健康.Duan等[1]中指出,太湖(中国第三大淡水湖)蓝藻的爆发时间一般为春夏两季,爆发区域由北部向南部扩散,并且蓝藻爆发的持续时间和波及区域正逐年增加.对蓝藻爆发的形成机制、演化规律及控制策略等方面的研究引起了众多学者的关注[2-4].
在浮游生物系统中, Prorocentrum,Coolia monotis,Gymnodinium breve等多种藻类会释放毒素至周围水体中,从而引起其他生物物种死亡率的增加.浮游植物释放的毒素在浮游植物与浮游动物相互作用过程中扮演着重要角色[5].文献[6-8]利用动力学建模的方法讨论了毒素释放对浮游生物系统演化和蓝藻爆发的影响.Pal等[6]研究了一类浮游生物模型,发现浓度较大的毒素可以抑制浮游植物和浮游动物种群浓度的振荡行为,从而对浮游生物系统具有稳定化作用.
Chattopadhayay等[5]提出了浮游植物释放毒素的浮游生物模型
(1)
式中:P=P(t)和Z=Z(t)分别为t时刻浮游植物种群和浮游动物种群的浓度;r和K分别为浮游植物种群的内秉增长率和环境容纳量;f(P)为浮游动物对浮游植物的捕食函数;c为生物量的转化系数;μ为浮游动物种群的自然死亡率;g(P)为浮游植物种群的毒素释放函数.
如果在模型(1)中选取f(P)=αP,g(P)=θP/(γ+P),并考虑浮游动物种群存在密度制约,可以得到模型
(2)
式中:θ为毒素释放率;α为浮游动物对浮游植物种群的捕食率;β为摄食率,β=cα;η为密度制约系数.
基于模型(2),进一步考虑浮游生物种群在某一自封闭的空间中扩散,可以得到具有Neumann边界条件的扩散模型
(3)
式中:P=P(x,t),Z=Z(x,t);Ω为具有光滑边界∂Ω的有界区域;ν为∂Ω的外法向单位向量;d1和d2分别为2个种群的扩散系数;假设上述模型中所有参数均为正常数.
首先分析常微分方程模型(2)的全局动力学行为,再讨论反应扩散模型(3)的全局动力学行为,重在揭示空间扩散对系统动力学的影响,并通过数值模拟验证所得结果的正确性.
2 模型(2)的全局动力学行为
定义集合
易知Γ为模型(2)的正向不变集.对于任意的参数,模型(2)总存在零平衡点E0(0, 0)和边界平衡点E1(K, 0).另外,当且仅当P* (4) 记 模型(2)平衡点的稳定性可以由如下Jacobin矩阵的特征值决定: 对于零平衡点E0(0, 0), 其特征值为r和-μ.所以,E0为鞍点. 对于边界平衡点E1(K, 0), 所以,当P* 当P* 由 可得Trac(J|E*)<0,Det(J|E*)>0.所以,E*局部渐近稳定.另外,构造Dulac函数 计算可得 综上所述,可得定理1. 定理1对于模型(2),零平衡点E0(0, 0)总存在,且为不稳定的鞍点;当P*>K时,模型不存在正平衡点,边界平衡点E1(K, 0)全局渐近稳定;当P* 由方程(3)可知,P=P(x,t)满足 结合文献[9]中的引理2.1和比较原理[10],可得 同理,当t充分大时,Z=Z(x,t)满足 即 另外,当t充分大时,P=P(x,t)满足 结合比较原理,可得 类似地,当t充分大时,Z=Z(x,t)满足 即 综上所述,可得定理2. 模型(3)的正平衡点E*的局部稳定性可以由如下的Jacobin矩阵的特征值决定: 式中,k2表示波数. 显然,当P* Trac(Jk2)=Trac(J|E*)-(d1+d2)k2<0 Det(J|E*)>0 综上所述,可得定理3. 群体大小对保育阶段猪的采食、饮水、排泄等影响不大,但对活动、争斗影响明显,以40头组发生打斗行为最少,20头组次之,10头组最高。 定理3当P* 比较定理2和定理3可以发现,扩散因素的存在不会改变E*的稳定性,即模型(3)不会出现Turing斑图. 为了证明模型(3)的正常稳态E*的全局稳定性,构造如下Lyapunov函数: 则 其中 由格林公式可得 另外, 显然,当 (5) dV/dt≤0,当且仅当(P,Z)≡(P*,Z*)时等号成立. 综上所述,可得定理4. 定理4当P* 从已有的调查实验和理论研究发现,浮游植物释放的毒素对浮游生物系统演化具有重要影响.本文首先分析了一类具有毒素释放的浮游生物模型的全局动力学行为.对于不考虑空间扩散的情形,证明了当P*>K时,正平衡点不存在,边界平衡点E1(K,0)全局渐近稳定;当P* 由方程(4)可知,P*关于参数θ单调递增.当浮游植物种群的毒素释放率θ增大时,P*会随之增大,并且会超过浮游植物种群的环境容纳量K,此时,浮游动物种群将趋于绝灭.所以,浮游植物释放的毒素不利于浮游生物系统的持久性.另外,由定理4可知,模型(3)不会出现Turing斑图,即扩散因素的存在不会改变浮游生物系统的稳定性. 为了验证所得的理论结果,选取与文献[11]中相同的参数进行数值模拟.取定r=1.5,K=17,α=0.063,β=0.038 7,μ=0.035,η=0.09,θ=0.1,γ=1.5,计算可得P*=13.766 5 图1 模型(2)的解曲线Fig.1 Solution curve of the model (2) 对于模型(3),取Ω=(0,5π),d1=0.01,d2=0.05,其他参数取值同上,可以验证 由定理3可知,模型(3)的正平衡点E*(13.766 5,4.528 8)是全局渐近稳定的.仿真结果如图2所示. 图2 模型(3)的解曲面Fig.2 Solution surface of the model (3) [1] DUAN H T,MA R H,XU X F,et al.Two-decade reconstruction of algal blooms in China’s Lake Taihu[J].Environmental Science & Technology,2009,43(10):3522-3528. [2] GUO L.Doing battle with the green monster of Taihu Lake[J].Science,2007,317(5842):1166. [3] 王成林.太湖蓝藻水华及藻源性“湖泛”形成机制的气象因素研究[D].南京:南京大学,2010. [4] CHEN M,FAN M,LIU R,et al.The dynamics of temperature and light on the growth of phytoplankton[J].Journal of Theoretical Biology,2015,385(2):8-19. [5] CHATTOPADHAYAY J,SARKAR R R,MANDAL S.Toxin-producing plankton may act as a biological control for planktonic blooms-field study and mathematical modelling[J].Journal of Theoretical Biology,2002,215(3):333-344. [6] PAL R,BASU D,BANERJEE M.Modelling of phytoplankton allelopathy with Monod-Haldane-type functional response—a mathematical study[J].Biosystems,2009,95(3):243-253. [7] LI J,SONG Y Z,WAN H,et al.Dynamical analysis of a toxin-producing phytoplankton-zooplankton model with refuge[J].Mathematical Biosciences and Engineering,2017,14(2):529-557. [8] BANERJEE M,VENTURINO E.A phytoplankton-toxic phytoplankton-zooplankton model[J].Ecological Complexity,2011,8(3):239-248. [9] SHI H B,LI W T,LIN G.Positive steady states of a diffusive predator-prey system with modified Holling-Tanner functional response[J].Nonlinear Analysis:Real World Applications,2010,11(5):3711-3721. [10] 叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1990. [11] CHATTOPADHYAY J,VENTURINO E,CHATTERJEE S.Aggregation of toxin-producing phytoplankton acts as a defence mechanism—a model-based study[J].Mathematical and Computer Modelling of Dynamical Systems,2013,19(2):159-174.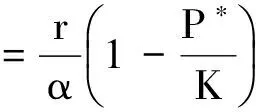




3 模型(3)的全局动力学行为
3.1 持久性
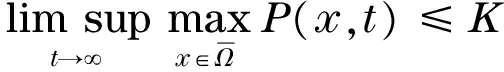



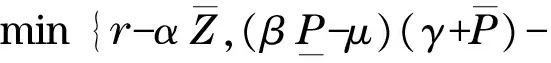
3.2 正平衡点E*的稳定性
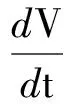
4 仿真与讨论


