基于小波消噪和优化支持向量机的板形模式识别

吴忠强 康晓华 于丹琦

燕山大学工业计算机控制河北省重点实验室，秦皇岛,066004

0 引言

板形是检测板带钢质量的重要指标，板形模式识别是板形控制系统的关键环节，如何有效地提高板形模式识别的精度成为现阶段板带研究的重点[1]。板形识别方法主要有最小二乘法[2]和神经网络方法[3-4]。最小二乘法的物理意义不明确，而且随着板形精度的提高多项式的系数和次数也会相应增加，使得处理过程复杂；神经网络方法的学习能力很强，但是容易陷入局部极值，对于未经训练的数据，泛化能力不强，收敛速度慢。

板形模式识别的智能优化方法中的粒子群算法简单易实现[5]，逼近最优解的速度快,但是粒子群算法容易过早收敛到局部极值。遗传算法是一种全局优化算法[6]，但遗传算法的编程较为复杂，对初始种群的依赖性较大，求解时间较长。相比于粒子群算法，万有引力优化算法的收敛速度快[7]，但其获得的最优解精度不高。

在实测的板形信号当中不可避免地会混入噪声信号，使得板形的识别精度下降。本文利用双变量阈值小波函数去噪，克服软硬阈值函数在处理小波系数方面存在的缺点[8-9]，得到更好的去噪效果。建立基于支持向量机(SVM)[10-11]的板形识别模型，利用布谷鸟优化算法对支持向量机的参数进行优化。

1 板形信号的基本模式

常见板形的基本模式分为以下8种：左边浪、右边浪、中间浪、双边浪、右三分浪、左三分浪、四分浪和边中浪。采用勒让德正交多项式表示板形的8种基本模式，则板形模式的归一化方程如下：

左边浪的标准归一化方程为

σ1=y

(1)

右边浪的标准归一化方程为

σ2=-y

(2)

中间浪的标准归一化方程为

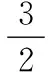
(3)

双边浪的标准归一化方程为

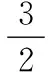
(4)

右三分浪的标准归一化方程为

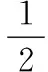
(5)

左三分浪的标准归一化方程为

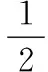
(6)

四分浪的标准归一化方程为

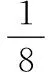
(7)

边中浪的标准归一化方程为

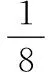
(8)

式中，y为归一化板宽，y∈[-1,1]；σi(i=1,2,…,8)为各种板形归一化的残余应力。

实际的板形通常是由上述基本板形模式线性组合而成的。由于同一种板形中互反的两种基本模式不能同时存在，故板形可以表示成：

Y(y)=μ1σ1+μ2σ3+μ3σ5+μ4σ7

(9)

其中，μ1、μ2、μ3、μ4代表实际板形所占的比例成分，它的取值既可以是正数也可以是负数，取值范围为[-1,1]。

2 基于小波分解的板形信号消噪

2.1 板形信号的小波分解与重构

用小波法对实际的板形信号去噪，实际上就是对原始的板形信号进行低通和高通滤波。一个含噪声的板形信号可以表示为

Y*(y)=Y(y)+ω

(10)

式中，Y*(y)为含噪声的板形信号；ω为噪声信号。

具体的分解与重构算法如下：

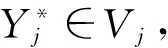
(11)

式中，L为小波变换分解的层数；j∈Z；φj,k(y)为尺度函数；cj,k为尺度系数(低频系数)；ψj-1,k(y)为小波函数；dj-1,k为小波系数(高频系数)。

(2)迭代。根据Mallat分解算法得到

(12)

(13)

式中，1≤l≤j，“-”表示共轭；hn-2k为低通滤波器系数；gn-2k为高通滤波器系数。

(3)重构。将处理后的系数采用Mallat合成公式进行板形信号的重构，即

(14)

经多次实验验证，采用三层分解并选择db4小波基函数时去噪效果较好。

2.2 基于双变量阈值小波函数的板形去噪

目前，小波去噪方法[12-14]主要可分为基于小波变换模极大值原理的小波去噪、基于小波系数相关性的小波去噪和阈值去噪三类。其中阈值去噪方法是一种简洁有效的去噪方法，本文将三种阈值消噪方法(硬阈值消噪、软阈值消噪和双变量阈值消噪)对板形的消噪效果进行比较。

硬阈值函数的表达式为

(15)

软阈值函数的表达式为

(16)

双变量阈值函数的表达式为

(17)

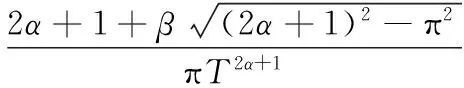
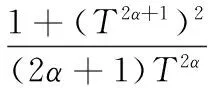
其中，α和β为调节因子。令α=1，β=0.8，阈值T=0.5，三种阈值函数如图1所示。

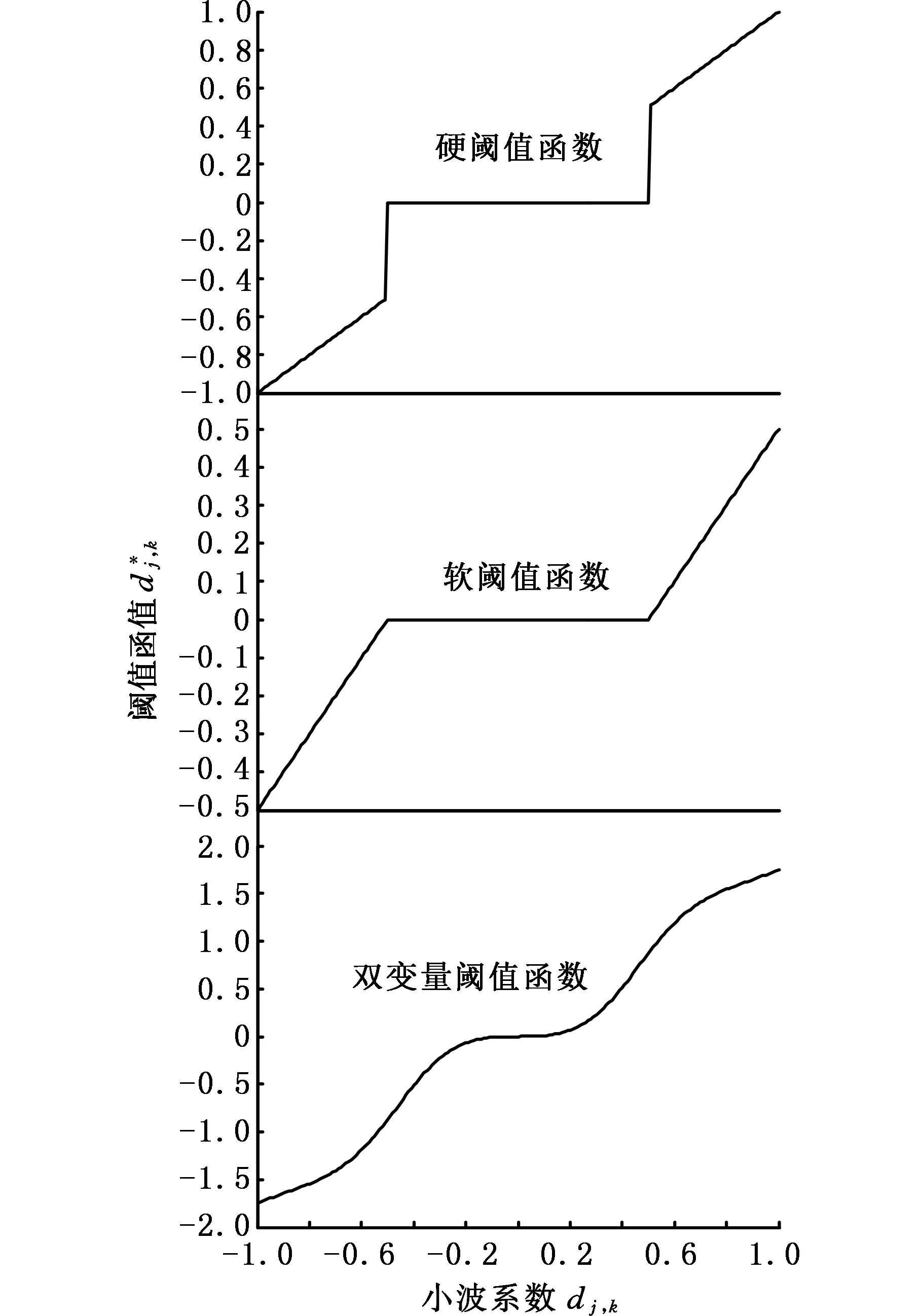
图1 三种阈值函数示意图Fig.1 Schematic diagram of three threshold function

硬阈值函数是将绝对值小于阈值的小波系数变成0，将绝对值大于阈值的小波系数予以保留。由此，处理后的小波系数在正负阈值处不连续，产生间断点，使重构后的信号产生振荡。

软阈值函数将绝对值大于阈值的小波系数不是完全保留而是做收缩处理，即减小这些系数值，因而软阈值函数很好地克服了硬阈值的缺点，但这种方法减小了绝对值大的小波系数，造成一定的信息损失。

双变量阈值函数在小波域内具有一定的连续性和高阶可导性。它在有用信号和噪声之间存在一个平滑过渡区，α和β作为调节因子，可使阈值函数在软硬阈值函数之间随意切换。α值越小，曲线越缓；α值越大，曲线越陡，所以α可用来调节去噪信号的平滑度。而β=-1时，阈值函数可视为软阈值函数的修正，并在α趋于无穷时，等效为软阈值函数；β=1时，阈值函数可视为硬阈值函数的修正，并在α趋近于无穷时，等效为硬阈值函数。

采用三种阈值函数对实际的板形信号进行滤波。实测带噪声的板形信号为

Y*(y)=0.1σ1+0.2σ3+0.3σ5+0.4σ7+ω

其示意图见图2，三种阈值函数的去噪结果如图3所示。

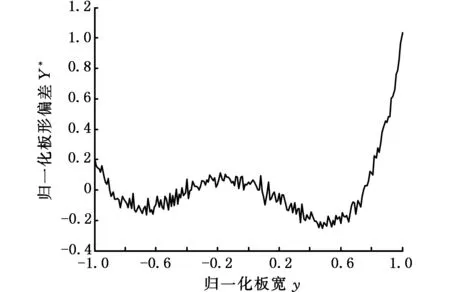
图2 带噪声的原始板形信号Fig.2 Original flatness signal with noise

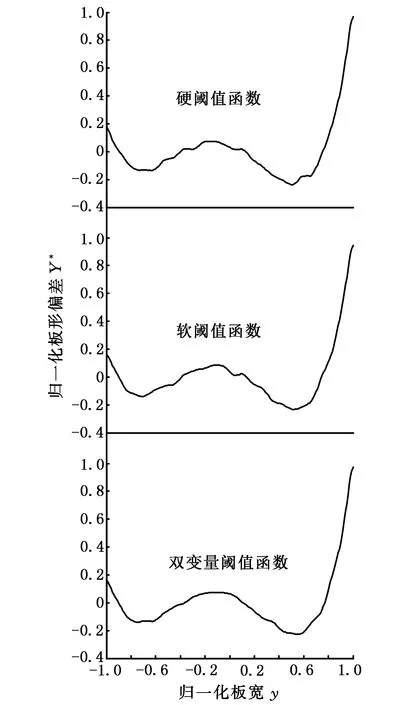
图3 三种阈值函数去噪结果Fig.3 Schematic diagram of the three thresholdde-noising

由图3可看出，双变量阈值函数去噪效果最好，去噪后的板形信号很平滑。为了更清楚地比较三者的去噪性能，采用信噪比RSN作为评价去噪性能指标：

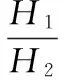
(18)

H1=sum((Y(y)-mean(Y(y)))2)

H2=sum((Y*(y)-Y(y))2)

式中，sum()、mean()分别为求和函数和求平均函数。

三种阈值函数的去噪结果如表1所示。由表1可看出，双变量阈值函数的信噪比最大，去噪效果最好。

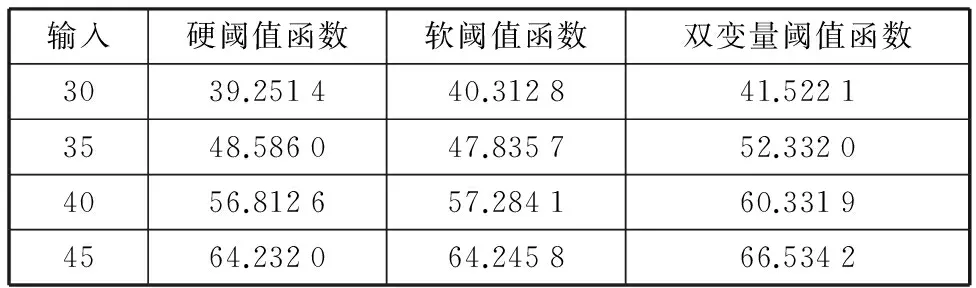
表1 三种去噪方法的信噪比RSN比较

3 基于优化支持向量机的板形识别

3.1 基于SVM的板形模式识别模型建立

对板形进行模式识别的过程其实就是将该板形所含有基本模式的比例成分识别出来,即将μ1、μ2、μ3、μ4的具体值识别出来。采用支持向量机进行板形模式识别的步骤如下。

(1)确定支持向量机的输入。由式(1)～式(8)可知，8种基本板形模式分为四组两两互反的模式，且识别出的板形中互反的两种模式不能同时存在，因此，可分别求出待识别样本与两个互反的基本模式的欧氏距离，将欧氏距离差作为支持向量机的输入。将实测板形的应力值离散化为

Y*(y)=(Y*(1),Y*(2),…,Y*(m))

(19)

m为离散化后的段数。将8种基本板形的应力值离散化为

σk(y)=(σk(1),σk(2),…,σk(m))k=1,3,5,7

计算出实测板形和每组基本板形互反模式的欧氏距离：

Sk=‖Y*-σk‖

Sk+1=‖Y*-σk+1‖

其欧氏距离的差

ηk=Sk-Sk+1

(2)对板形进行模式识别的问题可以转化为非线性回归问题，本文选用v-支持向量机，其具体步骤如下：

本文需要建立4输入4输出模型，采用4输入单输出的4个SVM实现。模型结构如图4所示。

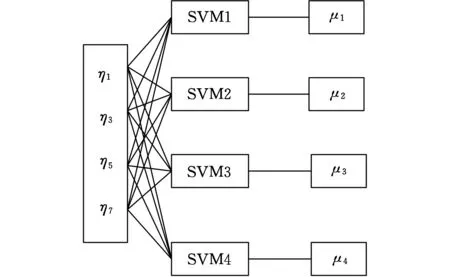
图4 基于支持向量机的模型结构Fig.4 Model structure based on support vector machine

以SVM1为例进行说明,训练样本集为

((ηi,μ1i)i=1,2,…,γ)

ηi=[η1η3η5η7]T

式中，γ为样本数目。

构造非线性回归函数

f(η)=w·φ(ηi)+b

式中，w、b为回归因子。

将板形模式识别问题转换为如下优化问题：

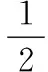
(20)

s.t.

(21)

其中，C为惩罚因子，对经验风险与置信范围两者进行折中，ξ和ξ*为松弛变量，ε为不敏感度，v>0。

引入拉格朗日函数可得式(20)的对偶形式：

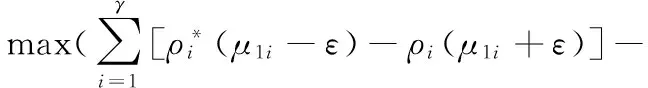
(22)

s.t.

(23)

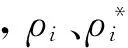
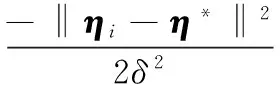
式中，δ为核宽度；η*为高斯分布的期望值。

求解上述优化问题，可推出SVM的输出函数：

3.2 布谷鸟搜索算法

布谷鸟搜索算法[15]是一种新的启发式优化算法。该算法简单易行、参数少，在处理复杂优化问题时无需重新匹配大量参数。事实上，除了种群数量χ之外，布谷鸟搜索算法只有一个参数，即外来鸟蛋被巢主鸟发现的概率Pa。

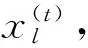
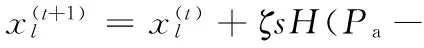
(24)

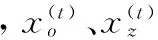
全局搜索过程可以描述为

(25)

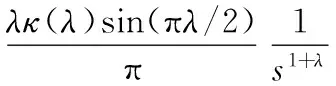
1<λ≤3

式中，κ(λ)为随机搜索步长。

3.3 布谷鸟搜索算法优化支持向量机(CS-SVM)参数的步骤

以布谷鸟算法优化SVM1的两个参数(惩罚因子C和核函数的宽度参数δ)，这两个参数对支持向量机的识别精度有着重要的影响。C越小代表经验误差惩罚越小，造成学习机器简单而经验风险大，出现欠学习的现象；惩罚参数大时，造成学习机器结构复杂而经验风险较小，出现过学习的现象。支持向量机中核函数的参数值δ越小，越容易造成过拟合现象，降低支持向量机的性能，其值较大时，会产生欠学习的现象。使用布谷鸟算法优化支持向量机的参数C和δ,使其学习能力以及泛化能力达到最优。优化步骤如下：

(1)设置初始概率Pa=0.25、迭代次数N,随机产生χ个鸟窝的位置xi,i=1,2,…,χ，每一个鸟窝位置对应一组参数(C,δ)，计算每组鸟窝位置对应的适应度值，本文的适应度取SVM输出与期望输出的均方误差(MSE)，其计算公式为

(26)

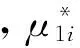
(2)根据式(24)、式(25)进行位置更新，并再次计算更新后的位置对应的适应度值，对比上一代鸟窝的位置，适应度值较好的位置进入下一代。

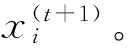
4 实验与分析

为了验证CS-SVM的优越性，将其与粒子群算法优化支持向量机(PSO-SVM)、遗传算法优化支持向量机(GA-SVM)作对比。将经过双变量阈值小波函数滤波的样本数据分为两类：一类样本是训练样本，并选择其中的20组样本进行回归识别测试；另一类样本是未训练样本，选取其中的10组样本进行回归识别测试。训练样本如表2所示。

设置布谷鸟算法的终止代数为100，鸟窝数量为25，巢主鸟能发现外来鸟蛋的概率为0.25；设置PSO算法的终止代数为100，粒子数目为20，认知系数c1为1.5，社会系数c2为1.7；设置GA算法的终止代数为100，交叉概率为0.5，变异概率为0.001，种群数量为20，仿真结果如表3和图5、图6所示。

表2 训练样本Tab.2 Training samples

由表3可知，CS-SVM的平均EMS为1.448 5×107，PSO-SVM的平均EMS为0.004 5，GA-SVM的平均EMS为1.600×103,CS-SVM的识别精度最高。由图6可看出，CS-SVM的最佳适应度达到0.002 030 8；PSO-SVM的最佳适应度达到0.019 964 6；GA-SVM的最佳适应度达到0.002 158 5，多次试验发现，每次运行GA，其最佳适应度收敛的速度变化很大，如图6c、图6d所示，说明该算法的稳定性差。上述结果表明CS-SVM不但精度高，而且收敛速度快。

对未训练的10组板形样本进行模式识别测试。未训练的样本数据如表4所示，其识别结果如表5所示。

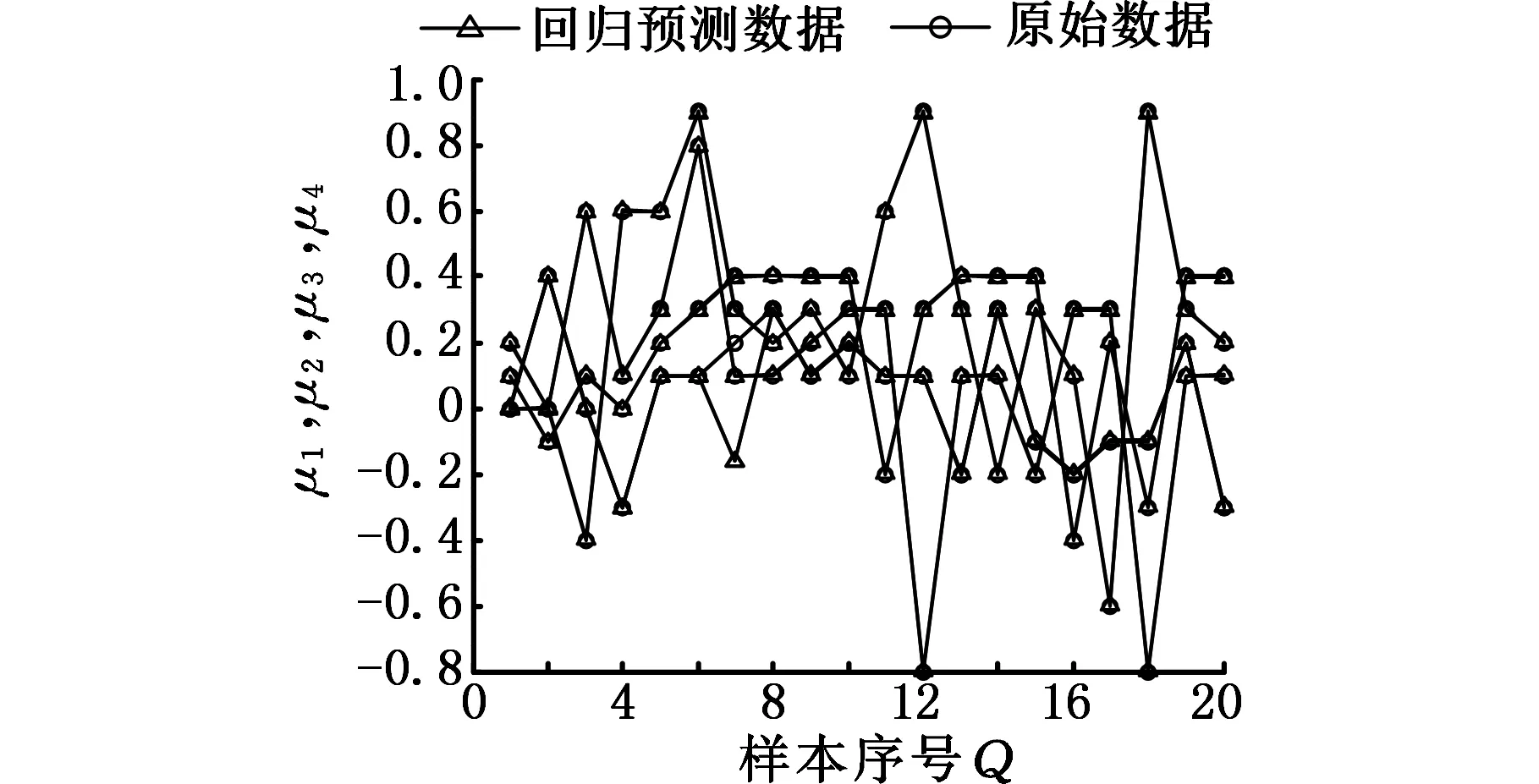
选取其中一组样本数据Y25=0.2σ1+0.3σ3+0.1σ5+0.6σ7作为代表，4种优化算法的拟合结果如图7所示。

由表5可知，CS-SVM的平均EMS为0.022 3；PSO-SVM的平均EMS为0.062 3；GA-SVM的平均EMS为0.096 7。从图7中也可看出，CS-SVM的拟合效果最好，说明CS-SVM的识别模型学习能力和泛化能力最强。

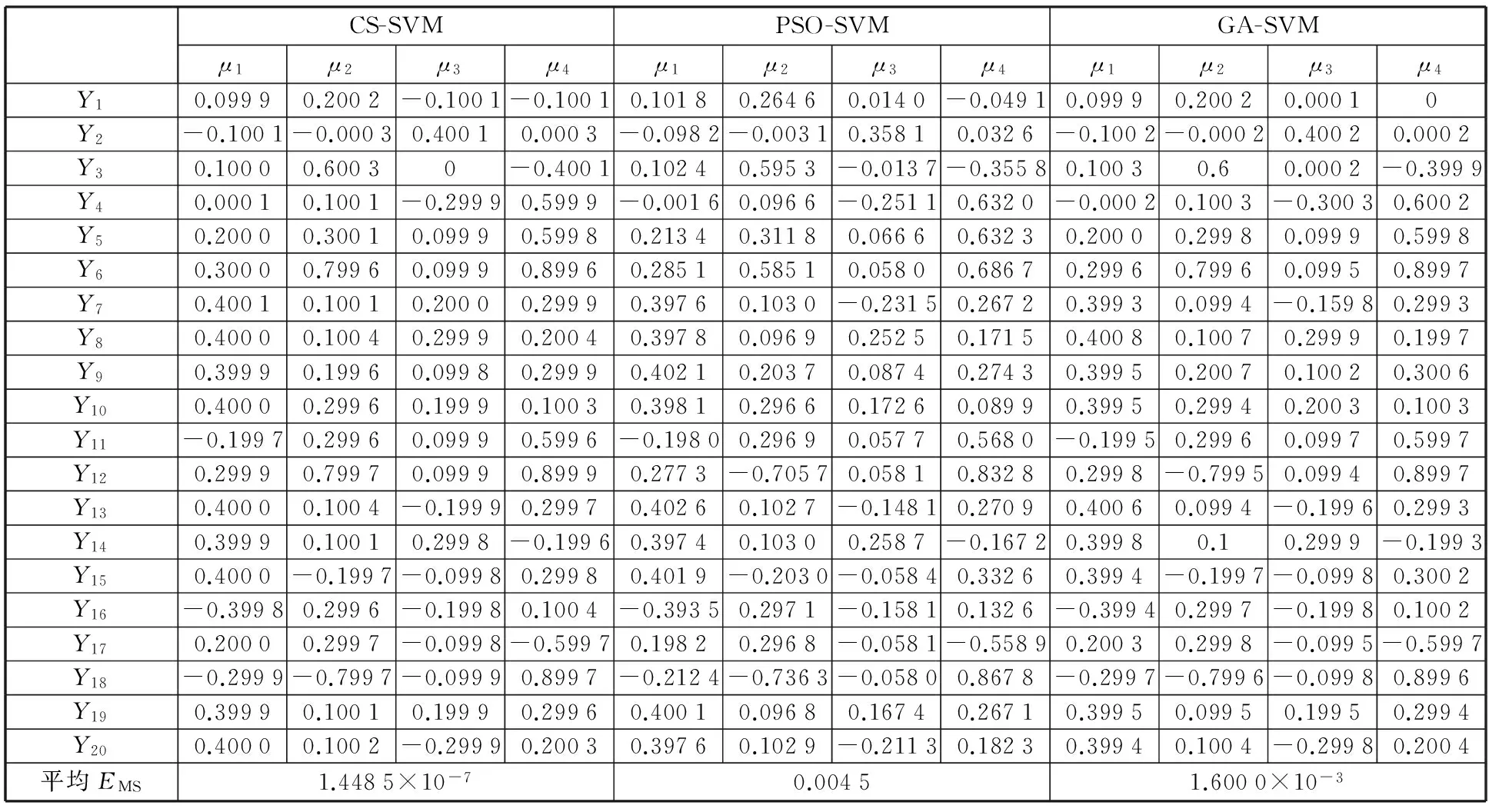
表3 训练样本的识别测试结果Tab.3 The recognition test results of training samples

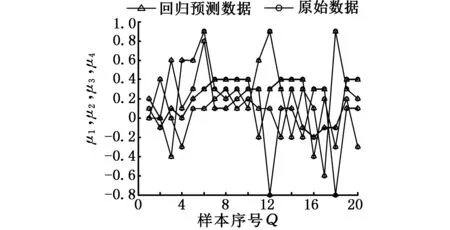
(a)CS-SVM

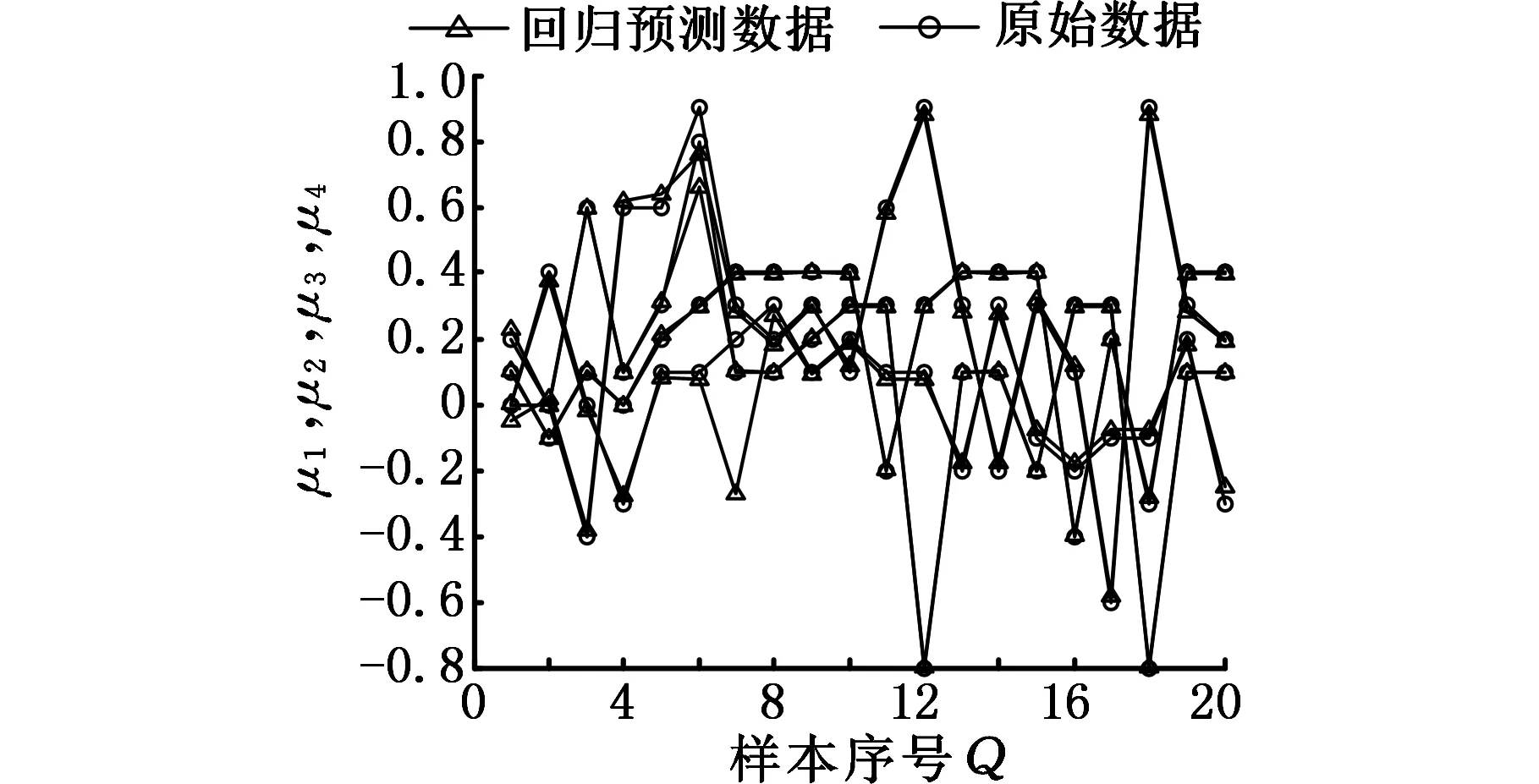
(b)PSO-SVM

(c)GA-SVM图5 三种方法的识别拟合图Fig.5 Identification fitting curves of the three methods

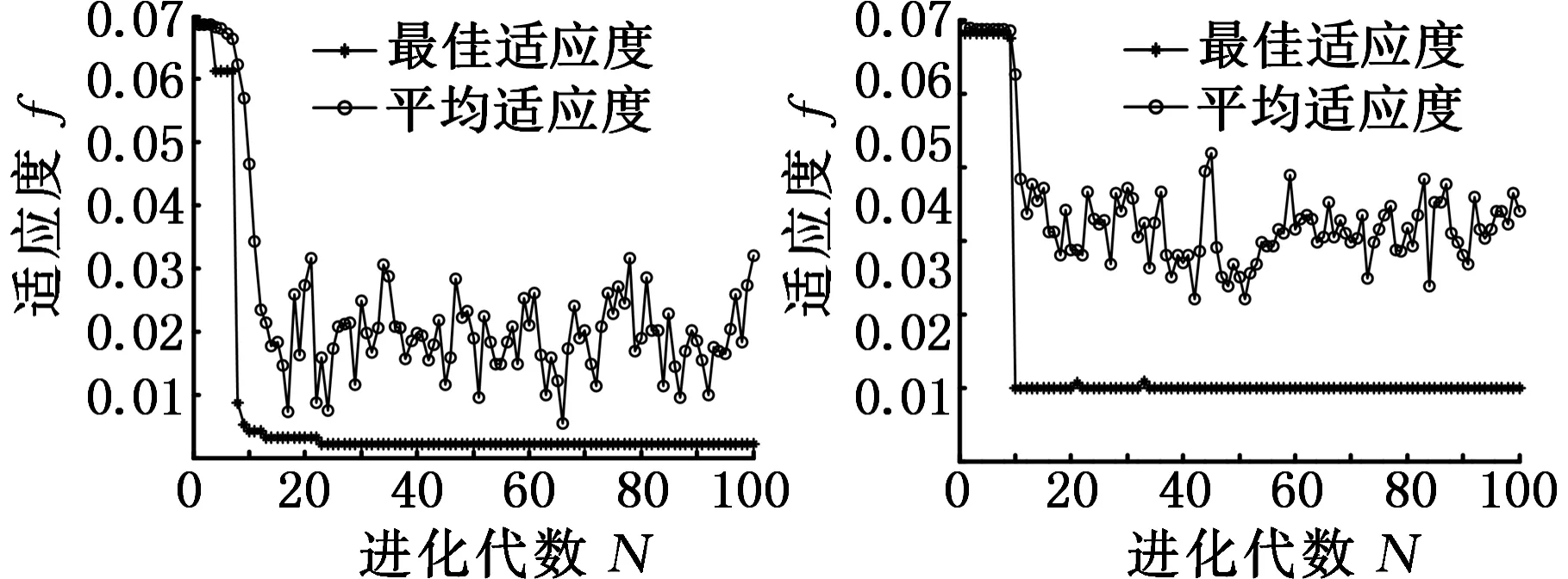
(a)CS-SVM (b)PSO-SVM

、

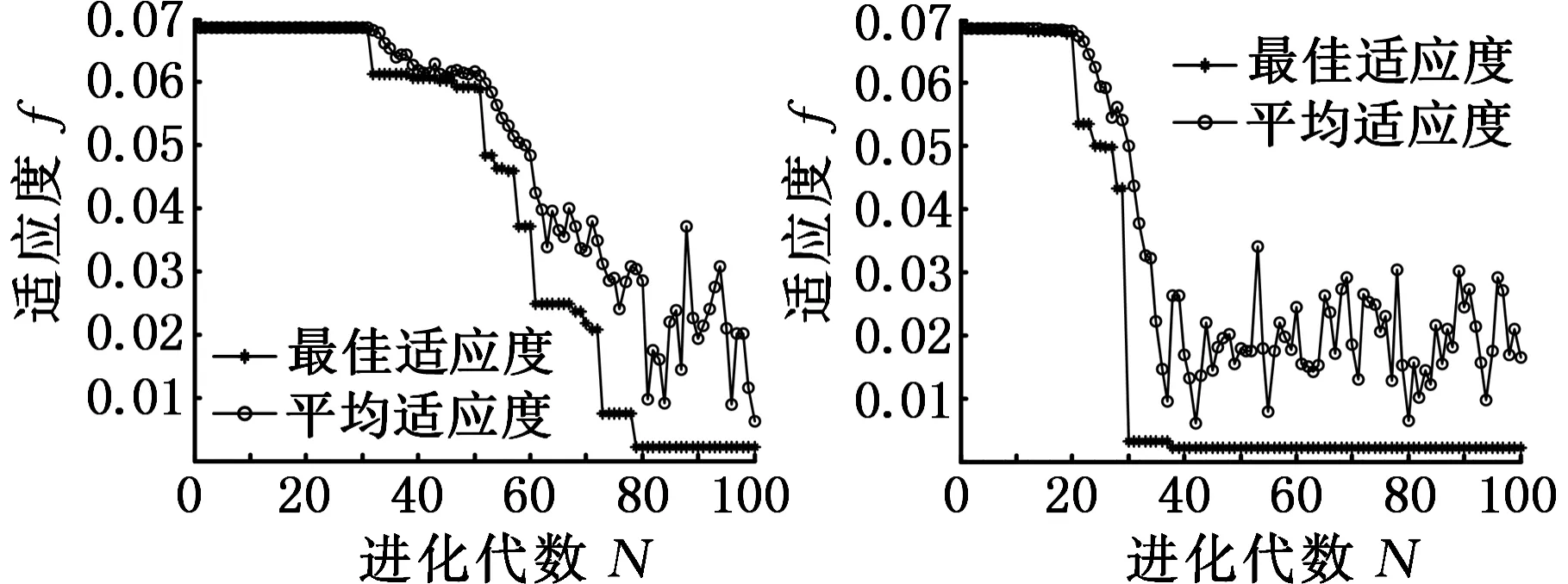
(c)GA-SVM (d)GA-SVM 适应度曲线图1 适应度曲线图2 图6 各寻优算法的适应度曲线图Fig.6 Fitness curve of each optimization algorithm

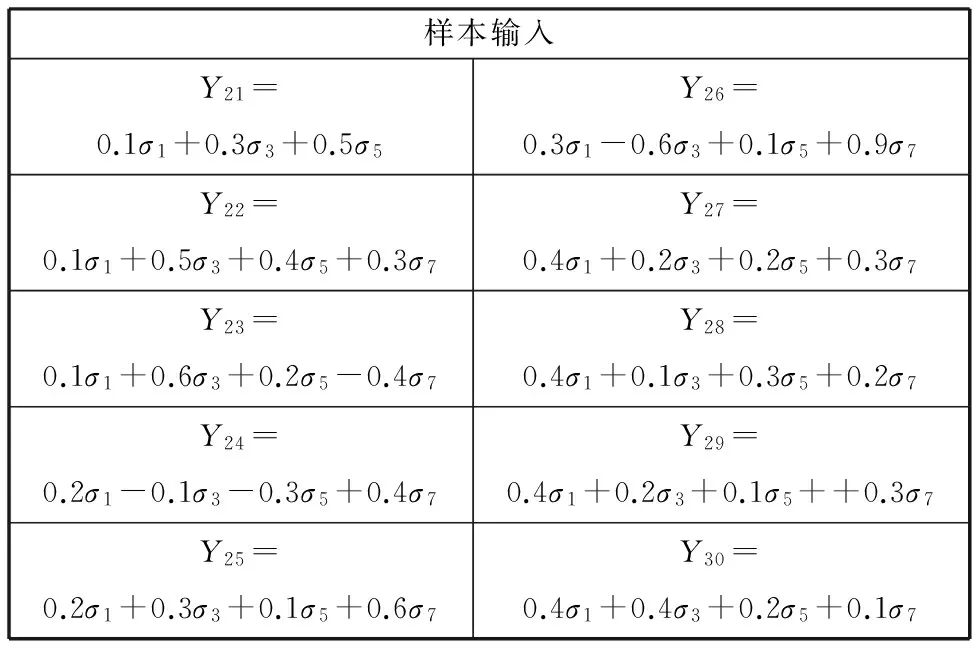
样本输入Y21=0.1σ1+0.3σ3+0.5σ5Y26=0.3σ1-0.6σ3+0.1σ5+0.9σ7Y22=0.1σ1+0.5σ3+0.4σ5+0.3σ7Y27=0.4σ1+0.2σ3+0.2σ5+0.3σ7Y23=0.1σ1+0.6σ3+0.2σ5-0.4σ7Y28=0.4σ1+0.1σ3+0.3σ5+0.2σ7Y24=0.2σ1-0.1σ3-0.3σ5+0.4σ7Y29=0.4σ1+0.2σ3+0.1σ5++0.3σ7Y25=0.2σ1+0.3σ3+0.1σ5+0.6σ7Y30=0.4σ1+0.4σ3+0.2σ5+0.1σ7

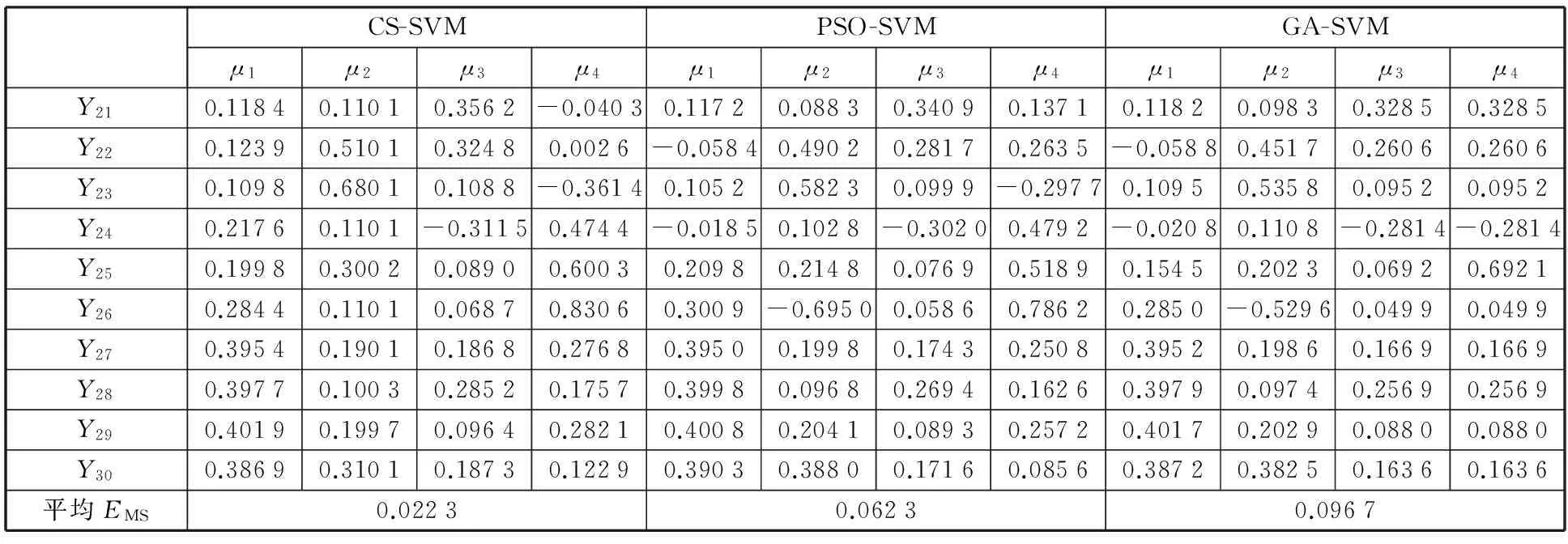
表5 未训练样本的识别结果

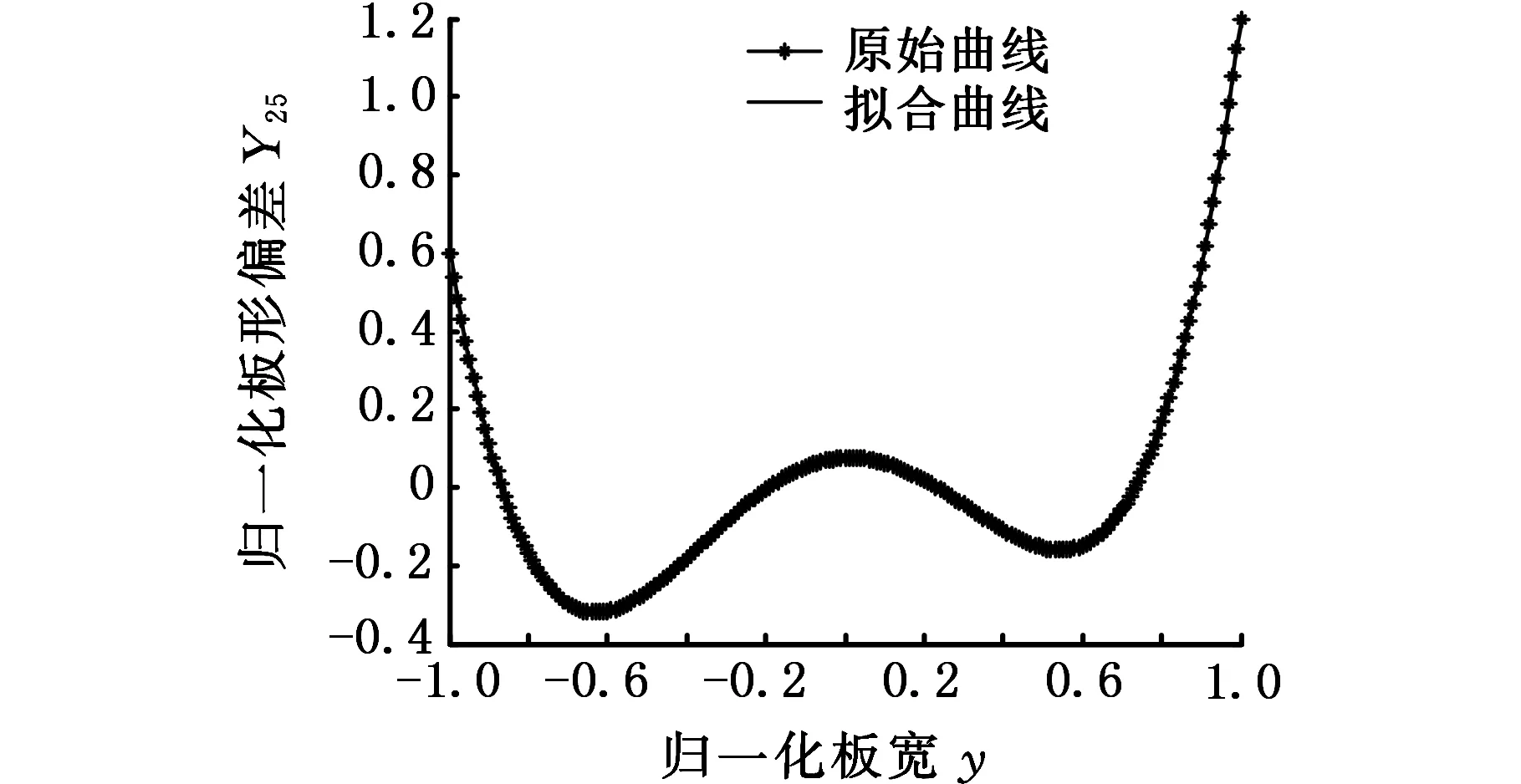
(a)CS-SVM拟合结果

(b)PSO-SVM拟合结果

(c)GA-SVM拟合结果图7 三种优化算法的拟合结果Fig.7 Fitting results of 3 optimization algorithms

下面对实测真实数据的识别结果进行对比分析。

某冷轧带钢厂的一组实测板形数据为[16]σ=(30.00, 22.29,19.83,16.71,16.80,17.31,16.98,10.59,0.270,0.000,0.054,0.252,3.840,6.09,8.370,13.41,16.62,16.41,12.93,12.18)，采用ABB板形仪(一种接触式、基于压磁传感器的板形仪)进行测量，测量段宽为52 mm，被轧带材宽度为1.04 m。由于内部张应力难于直接测量，故采用检测测量辊上的径向作用力Fi，再由下式进行换算：

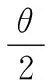
(27)

式中，a为测量段宽度;h为带材的厚度;σi为带材在第i段上的内部张应力;θ为包角值。

内部张应力σi在轧制过程结束后转变为残余内应力。

将实测板形张应力数据进行归一化处理，并应用上述三种结构模型进行仿真，识别结果如表6所示。

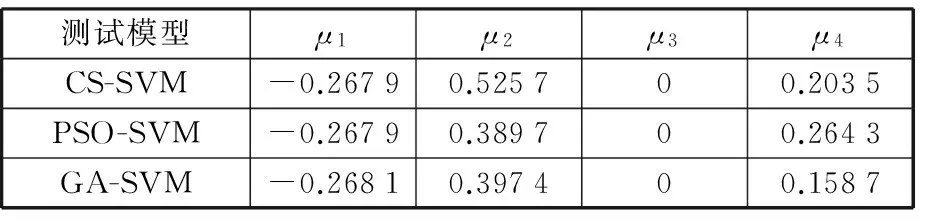
表6 实测数据仿真Tab.6 Simulation of measured data

由表6可知，4个分量中三次系数的分量为0，其他3个分量的仿真曲线如图8所示，其合成曲线如图9所示。

由表6可知，经计算，CS-SVM的EMS为0.012 7，PSO-SVM的EMS为0.017 9，GA-SVM的EMS为0.019 2。由图9可看出，三种方法都可以有效地将8种板形缺陷基本模式从实测数据中分离出来，CS-SVM的拟合效果最好，最接近真实信号。

5 结束语

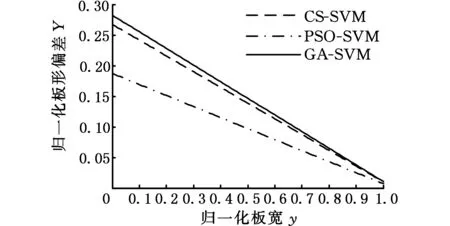
(a)一次分量

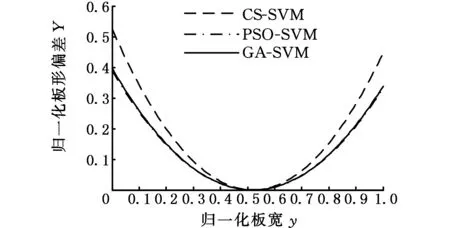
(b)二次分量

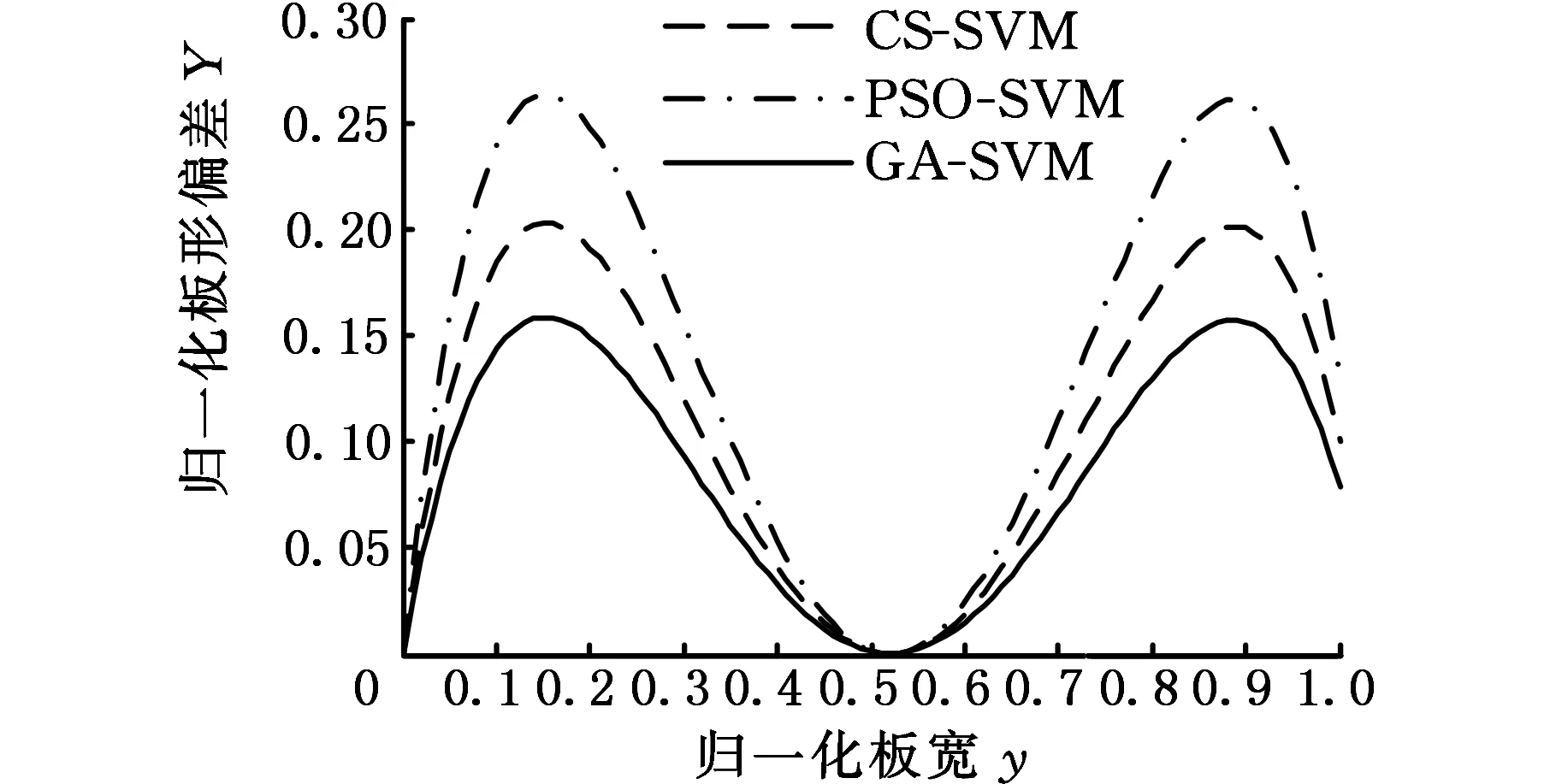
(c)四次分量图8 实测数据测试结果Fig.8 Test results of measured data

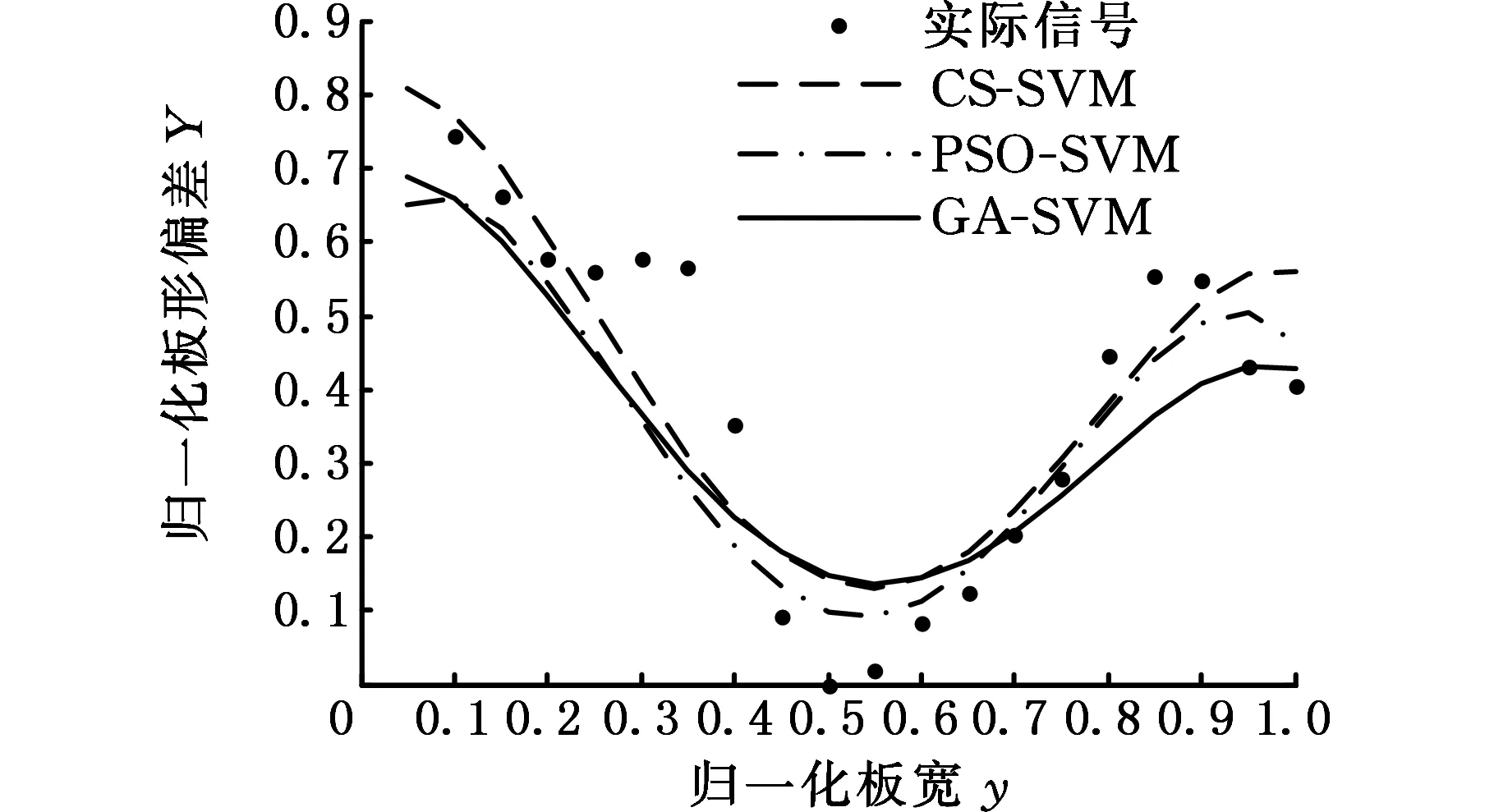
图9 实测数据拟合曲线Fig.9 Fitting curves of measured data

采用双变量阈值小波变换对实际采集到的板形信号进行消噪处理，有效地去除了噪声干扰。在此基础上采用布谷鸟优化支持向量机的识别模型进行识别，提高了板形识别的精度和收敛速度。相比于粒子群、遗传算法，布谷鸟优化算法的识别精度和收敛速度最佳。

[1] 单修迎, 刘宏民, 贾春玉. 含有三次板形的新型板形模式识别方法[J]. 钢铁,2010,45(8):56-60.

SHAN Xiuying, LIU Hongmin, JIA Chunyu. A Recognition Method of New Flatness Pattern Containing the Cubic Flatness[J]. Iron Steel,2010,45(8):56-60.

[2] 张秀玲, 刘宏民. 板形模式识别的 GA-BP 模型和改进的最小二乘法[J]. 钢铁,2003,38(10):29-34.

ZHANG Xiuling, LIU Hongmin. GA-BP Model of Flatness Pattern Recognition and Improved Least-squares Method [J]. Iron Steel,2003,38(10):29-34.

[3] 李海滨，高武杨，来永进，等. GA-T-S云推理网络板形模式识别的DSP实现[J].中国机械工程，2016,27(17):2341-2347.

LI Haibin, GAO Wuyang, LAI Yongjin, et al. Flatness Pattern Recognition via GA-T-S Cloud Inference Network Implemented by DSP [J]. China Mechanical Engineering,2016,27(17):2341-2347.

[4] ZHANG Xiuling, ZHAO Liang, ZHAO Wenbo, et al. Novel Method of Flatness Pattern Recognition via Cloud Neural Network[J]. Soft Computing,2015,19(10):2837-2843.

[5] 刘建昌, 陈莹莹, 张瑞友. 基于 PSO-BP 网络的板形智能控制器[J]. 控制理论与应用,2007,24(4):674-678.

LIU Jianchang, CHEN Yingying, ZHANG Ruiyou. Intelligent Flatness-controller Based on PSO-BP Network [J]. Journal of Control Theory and Application,2007,24(4):674-678.

[6] ZHANG Xiulin, CHENG Long, HAO Shuang, et al. The New Method of Flatness Pattern Recognition Based on GA-RBF-ARX and Comparative Research[J]. Nonlinear Dynamics,2016,83(3):1535-1548.

[7] 牛培峰, 李鹏飞, 李国强, 等. 基于万有引力优化的支持向量机模型在板形识别中的应用[J]. 钢铁,2012,47(12):45-49.

NIU Peifeng, LI Pengfei, LI Guoqiang, et al. Application of GSA-SVM Model in Flatness Pattern Recognition [J]. Iron Steel,2012,47(12):45-49.

[8] 宋君烈, 邵克勇, 迟德选, 等. 小波分析在板形缺陷识别中的应用[J]. 控制与决策,2002,17(1):69-72.

SONG Junlie, SHAO Keyong, CHI Dexuan, et al. Application of Wavelet Analysis in Recognizing the Defects of Plate Form in RollingProcess[J]. Control and Decision,2002,17(1):69-72.

[9] 黄敏, 董威, 徐林, 等. 基于小波分析和神经网络的板形模式识别方法[J]. 模式识别与人工智能,2005,18(1):103-106.

HUANG Min, DONG Wei, XU Lin, et al. Pattern Recognition for Flatness Based on Wavelet Analysis and Neural Networks[J]. Pattern Recognition and Artificial Intelligence,2005,18(1):103-106.

[10] ELBISY M S. Support Vector Machine and Regression Analysis to Predict the Field Hydraulic Conductivity of Sandy Soil[J]. KSCE Journal of Civil Engineering,2015,19(7):2307-2316.

[11] 杜树新, 吴铁军. 用于回归估计的支持向量机方法[J]. 系统仿真学报,2003,15(11):1580-1585.

DU Shuxin, WU Tiejun. Support Vector Machines for Regression [J]. Journal of System Simulation,2003,15(11):1580-1585.

[12] 张淑清, 胡永涛, 姜安琦，等. 基于双树复小波和深度信念网络的轴承故障诊断[J]. 中国机械工程,2017,28(5):532-543.

ZHANG Shuqing, HU Yongtao, JIANG Anqi. Bearing Fault Diagnosis Based on DTCWT and DBN [J]. China Mechanical Engineering,2017,28(5):532-543.

[13] 张淑清, 师荣艳, 董玉兰, 等. 双变量小波阈值去噪和改进混沌预测模型在短期电力负荷预测中的应用[J]. 中国电机工程学报,2015,35(22):5723-5730.

ZHANG Shuqing, SHI Rongyan, DONG Yulan, et al. Bivariate Wavelet Threshold De-noising and Improved Chaotic Forecasting Model and Its Application in Short-term Power Load Forecasting[J]. Journal of Chinese Electrical Engineering Science,2015,35(22):5723-5730.

[14] 刘卫东, 刘尚合, 胡小锋, 等. 小波阈值去噪函数的改进方法分析[J]. 高电压技术,2007,33(10):59-63.

LIU Weidong, LIU Shanghe, HU Xiaofeng, et al. Analysis of Modified Methods of Wavelet Threshold De-noising Functions [J]. Journal of High Voltage Technology,2007,33(10):59-63.

[15] 薛浩然, 张珂珩, 李斌, 等. 基于布谷鸟算法和支持向量机的变压器故障诊断[J]. 电力系统保护与控制,2015,43(8):8-13.

XUE Haoran, ZHANG Kehang, LI Bin, et al. Fault Diagnosis of Transformer Based on the Cuckoo Search and Support Vector Machine [J]. Journal of Power System Protection and Control,2015,43(8):8-13.

[16] 刘玠. 冷轧生产自动化技术[M]. 北京：冶金工业出版社,2006:116.

LIU Jie. The Cold Rolling Production Automation Technology[M]. Beijing: Metallurgical Industry Proess,2006:116.