基于遗传算法与最小最大优化方法的六自由度放疗床参数辨识方法
2018-01-16杨诗怡张峰峰孙立宁
李 松 杨诗怡 张峰峰 孙立宁
1.苏州大学机电工程学院,苏州,2150002.苏州大学苏州纳米科技协同创新中心,苏州,215123
0 引言
全世界每年因肿瘤死亡的人数持续上升,而我国因恶性肿瘤而导致死亡的概率在世界上处于较高水平,目前已经成为城市居民的第一死因[1]。目前,治疗肿瘤的三种主要方法为手术、放射和药物治疗[2]。随着放疗技术和设备的发展以及人们对肿瘤认识的不断深入,放射治疗已成为治疗恶性肿瘤的主要手段之一[3]。目前国外的治疗床大多数为串联结构,只能实现3个方向的移动,各个关节误差的积累导致定位精度较低,且无法达到精确放疗的治疗效果[4-7],因此,提高放疗床的定位精度具有很大的现实意义。
本文研究的6-HTRT构型放射治疗床为多支链并联机构,由于各个支链都存在加工和装配误差,直接导致该机构末端的定位精度不高。为了提高放疗床的绝对定位精度,就需要对机构模型进行参数辨识以实现标定。DAZRODRGUEZ等[8]运用加权最小二乘法,对并联机构模型进行了参数辨识;THANH等[9]提出了一种基于直接搜索技术的动力学参数辨识方法;CHEN等[10]提出了一种基于准牛顿法与粒子群优化算法的参数辨识方法。这些参数辨识方法往往需要知道系统的结构,具有很大的局限性,而传统的遗传算法虽然不依赖于系统结构,但具有收敛速度慢和早熟的缺点。
针对以上问题,本文提出了一种遗传算法与最小最大算法相结合的参数辨识方法。通过测量机构的位姿信息,建立机构的标定模型,再利用激光跟踪仪测得的并联机构实际位姿来对模型进行辨识,并用辨识出的参数对各运动控制器中的理论运动距离进行修改,最后通过绝对定位精度实验和重复定位精度实验来验证本文参数辨识方法的可行性。
1 标定模型的建立
1.1 放疗床结构
图1为放疗床实物图。放疗床通过虎克铰、十字轴、连杆来实现定平台与动平台的连接,并通过丝杠和滑块实现动平台6个自由度的运动。图2所示为放疗床坐标系。Bi、Pi(i=1,2…,6)分别为定平台和动平台的虎克铰中心点。在B点建立基座坐标系Bxyz,简计为{B},在P点建立与动平台固连的坐标系PxPyPzP,简计为{P},两坐标系z轴均与初始状态下的动定平台垂直,x轴与动定平台平行,y轴与导轨平行。

图1 6-HTRT放射治疗床Fig.1 Radiotherapy bed of 6-HTRT
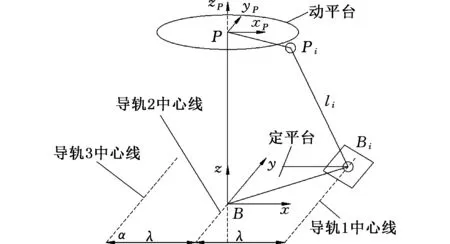
图2 放疗床坐标系Fig.2 Coordinate system of radiotherapy bed
1.2 测量方法和待标定参数的选取
由于在加工和安装过程中存在误差,故放疗床在运动时无法达到理想位置,因此,需要对其进行标定,以实现精确放疗。
本文中对放疗床的运动学标定使用了外部标定法,即利用激光跟踪仪来获取动平台上点的坐标,以计算出位置和姿态。在建立放疗床标定模型时,通过对放疗床进行误差分析,将影响放疗床末端位姿的主要结构参数考虑进来。对于每条支链考虑如下影响因素:基座坐标系中定平台虎克铰中心点坐标的坐标值x、y、z;动平台坐标系中动平台虎克铰中心点坐标的坐标值x、y、z;连杆两端的虎克铰中心点之间的距离即连杆长度l;基座坐标系中对应滑块的单位方向矢量的坐标值x、y、z。由于各支链均有10个待辨识参数,故放疗床6条支链共计有60个待辨识参数。
1.3 基于运动学逆解的标定模型建立
将对放疗床动平台位姿误差影响最大的60个待辨识参数运用于待建立的运动学逆解标定模型中,并需要在放疗床的工作空间内选取一些待标定的位姿点,将激光跟踪仪测得的位姿代入标定模型中,就可以得到60个待辨识的参数。
当动平台处于任意位姿时,基座坐标系中动平台虎克铰中心点的坐标可以表示为
BPi=BQPPPi+P
(1)
即具体表达式为
(2)
当放疗床处于一个给定的空间位姿时,考虑单个支链的坐标,可以得到表达式如下:
(BPix-hiai-BB0ix)2+(BPiy-hibi-BB0iy)2+
(BPiz-hici-BB0iz)2-|li|2=0
(3)
i=1,2,…,6
式中,BPi=(BPix、BPiy、BPiz)为基座坐标系{B}下动平台铰链中心点Pi的坐标值;BQP为绕基座坐标系x、y、z轴顺次转动θx、θy、θz得到的旋转变换矩阵;PPi为动平台虎克铰中心点Pi的矢量描述;P为动平台坐标系{P}下动平台铰链点所在圆的圆心坐标;BB0ix、BB0iy、BB0iz分别为初始状态在基座坐标系{B}中第i条支链定平台虎克铰中心点的坐标值;hi为沿导轨移动的距离,可从电机编码器读取;li为第i根连杆的方向向量,li=BPi-BBi;(ai,bi,ci)为基座坐标系中导轨的单位方向矢量。
想要求出60个待辨识参数,理论上只需给定10个放疗床工作空间内的位姿点即可。但实际上,由于标定模型中的方程组是多元且非线性的,且该并联机构为多输入、强耦合系统,想要准确辨识出放疗床真实的结构参数,只给出10个工作空间内的位姿点是远远不够的,因此在实验中需要给定更多的位姿,通过求解非线性超定方程组来寻求待辨识参数的最优解。
2 参数辨识方法
要实现放疗床的标定,以及提高放疗床的定位精度,就要对上述标定模型中的60个参数进行辨识,将辨识出的新参数代入控制器中,以得到与理论位姿差值更小的实际位姿。本文中的放疗床为多输入、多输出、强耦合、非线性的并联机构。上述建立的误差模型为多变量的非线性方程组[11],因此,本文中放疗床的结构参数的辨识问题可以等效为非线性方程组最优解的求解问题。遗传算法可以保证各方程残差总和达到较小的范围,可从整体上控制残差,但不可避免地会有极个别方程产生较大残差。由此,本文提出一种参数辨识方法,将遗传算法与最小最大优化方法相结合,可在控制单个方程残差较小的情况下减小整体残差,使所辨识出的参数更接近于真实值,从而有效提高放疗床的精度。
2.1 遗传算法与最小最大优化法相结合的参数辨识方法
应用传统遗传算法进行优化的一个关键问题在于适应度函数的选取。当给定一空间位姿时,设定机构的约束方程为[12-13]
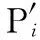
(4)
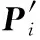

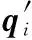
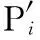
为了构造目标函数,现将式(3)进行变形:
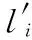
(5)
在式(5)中代入动坐标系中动平台虎克铰中心点的坐标,可得到
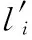
(6)
通过使用激光跟踪仪测量动平台上靶球的位姿数据,可得到动平台运动到不同空间位姿时,式(6)中相应点的θx、θy、θz和(Px,Py,Pz)T的值。
对放疗床的各个分支构造目标函数:
(7)
式中,ρi为目标函数中各方程所占权值,这里设置为1;n为选取标定点的数量。
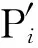
虽然上述方法辨识出来的参数能够实现残差最小的优化目标,但仍存在极个别方程残差较大的情况。并联机构的性质导致其每一个参数都可能对放疗床的整体精度产生很大的影响。为了改进遗传算法存在的不足,需要将每个方程的单独残差控制在一定范围内,故采用了最小最大优化方法,即控制所有方程的残差中绝对值最大的单独残差fij,使其最小化,可构造目标函数如下:
Q=min max(|fij|)
(8)
i=1,2,…,6j=1,2,…,n
最后,用MATLAB对上述问题进行优化,将上一步遗传算法中所得辨识值作为Fminimax函数的初值,对单个残差方程限制了其残差的最大值。将遗传算法与最小最大优化方法的优点相结合,可以将标定后的误差控制在较小范围内,提高放疗床的整体精度。
2.2 误差补偿模型建立
在得到放疗床的实际模型参数之后,可以对放疗床标定模型的参数进行修正。基座坐标系中各滑块对应导轨的单位矢量满足如下关系:
(9)
原方程组通过变形可以得到6个关于hi的二元一次方程:
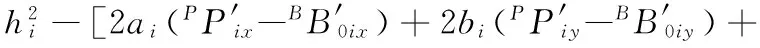
(10)
令
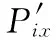
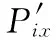
将辨识出的60个模型的实际参数代入式(10),由于丝杠行程受到限制,因此只有其中一组解能够满足要求,即
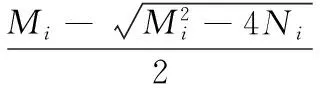
(11)
式(11)为放疗床实际逆解模型。通过代入放疗床在工作空间内的理论位姿后,经计算可使放疗床按照修正后的电机实际输入值进行运动,最后,通过激光跟踪仪可计算出放疗床实际位姿与理论位姿的差值,并进行精度验证[14]。
2.3 标定参数求解
标定算法是基于运动学逆解建立的,因此,求解待辨识参数时,需要测量放疗床的实际位姿,同时可以通过伺服电机的编码器得到机构6个滑块沿导轨方向的实际移动量。
本文将待辨识量的理论值作为初值,用上述基于遗传算法与最小最大优化法相结合的参数辨识方法对实际的结构参数进行了辨识,如表1所示。经辨识后的参数如表2所示,表中各参数的单位均为mm。
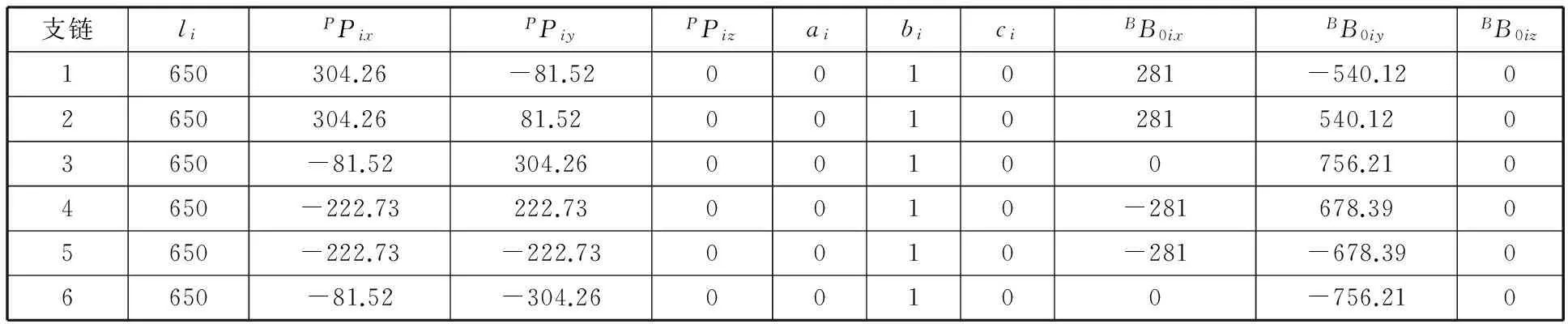
表1 待辨识参数理论值Tab.1 Theoretical value of parameters to be identified mm
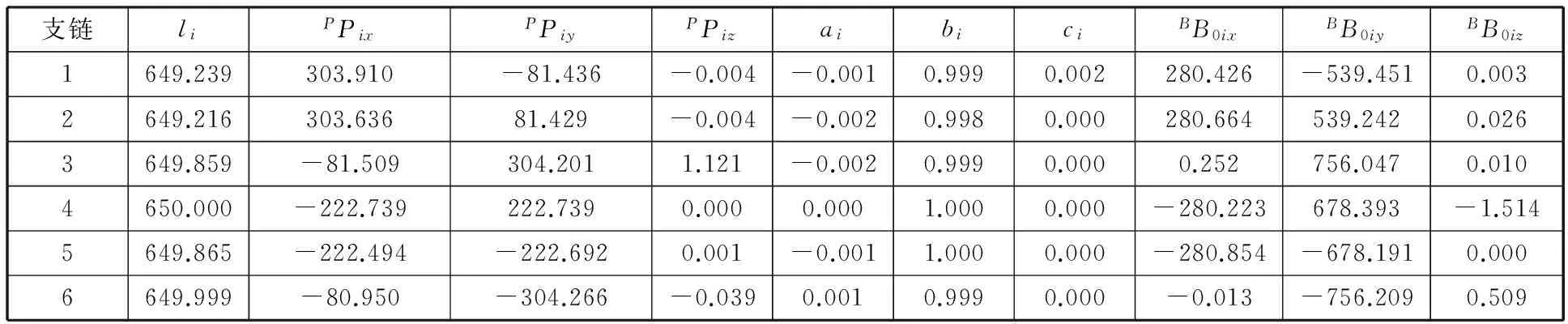
表2 辨识后参数值Tab.2 Parameters after identified mm
3 标定结果验证
3.1 标定实验平台
图3所示为标定实验平台,由放疗床、激光跟踪仪、控制柜组成,通过测量靶座坐标可以得到动平台的位姿数据。

图3 标定实验平台Fig.3 Calibration experiment platform
为了对理论分析进行验证,在标定实验平台的工作空间内任意选取若干组位姿点,分别测量参数修正前后放疗床的位姿数据,将参数修正前后测得的数据与理论值进行对比,用来对标定理论进行验证。另外,进行了重复定位位置精度实验,对放疗床标定前后位姿重复性位置精度进行了测量,以进一步验证参数辨识方法的正确性。
3.2 空间位姿点绝对定位精度验证
为了验证定位精度,在放疗床的工作空间内任意选取16组空间位姿点,针对放疗床x、y、z三个方向的移动和θx、θy、θz三个方向的转动进行了标定前后误差的测量和比较。使放疗床运动到16组位姿点,将测得的各位姿与理论值对比,得到标定前后放疗床沿各个自由度的误差,如图4所示。由图4可以看出,经过标定后16组任意位姿下放疗床的绝对定位精度有了很大的提高,沿着x、y、z三个方向的误差小于0.3 mm,绕x、y、z各轴的转角误差小于0.1°。由此,使用遗传算法与最小最大优化算法相结合的参数辨识方法对参数进行标定,可有效提高放疗床的整体定位精度。
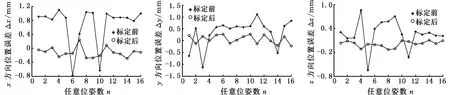
(a)x方向位置误差标定前后对比 (b)y方向位置误差标定前后对比 (c)z方向位置误差标定前后对比
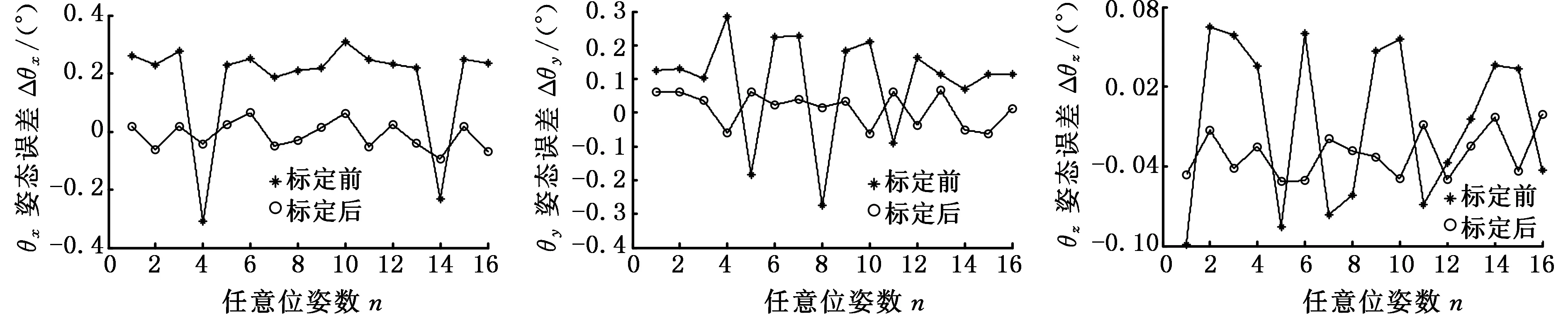
(d)θx姿态误差标定前后对比 (e)θy姿态误差标定前后对比 (f)θz姿态误差标定前后对比图4 16组任意位姿标定前后各自由度误差对比Fig.4 Error comparison of the degree of freedom before and after calibration for 16 free-position
3.3 放疗床重复定位位置精度测量
衡量放疗床性能的另一项重要指标是重复定位位置精度。选取上述16组任意位姿中的第1组,在同样的实验环境中使放疗床重复运动到指定位姿点15次,使用激光跟踪仪测得每次放疗床的实际位姿,以第一次的位姿点为基准,可得到位置误差分布如图5所示。
由图5可以看出,重复定位位置精度沿x轴方向小于0.002 5 mm,沿y轴方向小于0.002 mm,沿z轴方向小于0.003 mm,该精度可满足实际使用中对放疗床的精度要求,上述参数辨识方法得到了进一步验证。
由于载荷不同而导致零件具有不同的变形量,对放疗床的定位精度也会有一定的影响,因此还需要对治疗床进行刚度分析。当施加不同载荷时,可以将其等效为作用在动平台中心的力和力矩,根据力的大小和范围进行分组,按组分别建立补偿模型。以上工作将在以后的研究中进行,以提高放疗床在不同载荷下的定位精度。
4 结论
为了使六自由度放疗床达到精确放疗的治疗效果,本文基于运动学逆解建立了放疗床的标定模型,并提出了遗传算法与最小最大优化方法相结合的参数辨识方法,然后建立了误差补偿模型,实现了对控制器中参数的补偿。实验结果表明,经过标定后放疗床的绝对定位精度位置误差小于0.3 mm,姿态误差小于0.1°,而重复定位位置误差小于0.01 mm,满足指标要求。
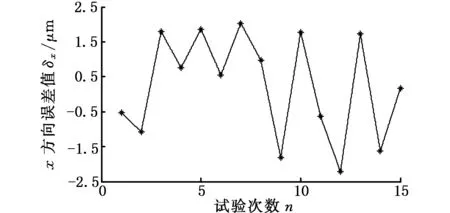
(a)x轴方向重复定位位置精度
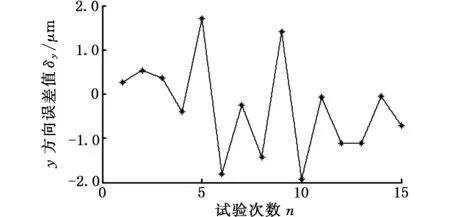
(b)y轴方向重复定位位置精度
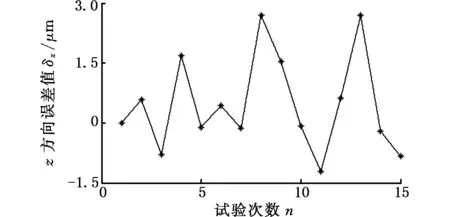
(c)z轴方向重复定位位置精度图5 放疗床重复定位位置精度Fig.5 Repetitive location accuracy of radiotherapy bed
[1] 魏沙. 2002~2010年我国城市恶性肿瘤死亡率变化趋势分析[J]. 实用预防医学,2013, 20(1):111-113.
WEI Sha. Analysis of Mortality Trend of Malignant Tumor in China in 2002-2010 Years[J]. Practical Preventive Medicine,2013,20(1):111-113.
[2] 刘泰福. 放射治疗在肿瘤综合治疗中的地位[J]. 中华肿瘤杂志,2010,32(8):638-639.
LIU Taifu. The Role of Radiotherapy in the Comprehensive Treatment of Tumors[J]. Chinese Journal of Oncology,2010,32(8):638-639.
[3] 于金明. 肿瘤放射治疗——已知与未知[J]. 医学争鸣,2012,3(6):4-6.
YU Jinming. Radiation Therapy for Tumors: Known and Unknown[J]. Negative,2012,3(6):4-6.
[4] SPEZI E, FERRI A. Dosimetric Characteristics of the Simens IGRT Carbon Fiber Tabletop[J]. Medical Dosimetry,2007,32(4):295-298.
[5] SINCLAIR J, CHANG S D, GIBBS I C, et al. Multisession Cyberknife Radiosyrgery for Intramedullary Spinal Cord Arteriovenous Malformations[J]. Neurosurgery,2006,58(6):1081-1089.
[6] GONG Hanshun, JU Zhongjian, XU Shouping, et al. G4 Cyberknife: New Instrument for Stereotactic Radiosurgery and Its Clinical Application[J]. Instrument Theory,2013,34(4):127-129.
[7] 陈万忠. 精确放射治疗床[J].医疗装备,2006(10):103.
CHEN Wanzhong. Precision Radiotherapy Bed[J]. Chinese Journal of Medical Device,2006(10):103.
[9] THANH T D, KOTLARSKI J, HEIMANN B, et al. Dynamics Identification of Kinematically Redundant Parallel Robots Using the Direct Search Method[J]. Mechanism & Machine Theory,2012,55(52):104-121.
[10] CHEN C T. Hybrid Approach for Dynamic Model Identification of an Electro-hydraulic Parallel Platform[J]. Nonlinear Dynamics,2011,67(1):695-711.
[11] 梁顺攀,郭联合,段艳宾,等.6-PUS/UPS并联机构运动学标定理论与实验研究[J].机械设计,2012,29(5):21-26.
LIANG Shunpan, GUO Lianhe, DUAN Yanbin, et al. Theory and Experiments on Kinematics Calibration of a 6-PUS/UPS Parallel Mechanism[J]. Journal of Machine Design,2012,29(5):21-26.
[12] 潘芳伟, 段志善, 贺利乐,等. 基于遗传算法的新型六自由度并联机器人运动学分析[J]. 机械科学与技术,2007,26(6):770-774.
PAN Fangwei, DUAN Zhishan, HE Lile, et al. Kinematics Analysis of a Novel 6-DOF Parallel Platform Manipulator Using Genetic Algorithm[J]. Mechanical Science and Technology for Aerospace Engineering,2007,26(6):770-774.
[13] 王朋, 段志善, 贺利乐. 基于遗传算法的并联机器人运动学正解研究[J]. 机械科学与技术,2005,24(8):956-959.
WANG Peng, DUAN Zhishan, HE Lile. Research of the Forward Kinematics of Parallel Robot Using Genetic Algorithm[J]. Mechanical Science and Technology for Aerospace Engineering,2005,24(8):956-959.
[14] 张宪民, 刘晗. 3-RRR 并联机器人含间隙的运动学标定及误差补偿[J]. 华南理工大学学报(自然科学版),2014,42(7):97-103.
ZHANG Xianmin, LIU Han. A Clearance Approach of Kinematic Calibration and Error Compensation for 3-RRR Parallel Robot[J]. Journal of South China University of Technology (Natural Science Edition),2014,42(7):97-103.
