面向故障诊断的行星齿轮扭振信号测量与分析

王 轩 王细洋

1.南昌航空大学飞行器工程学院，南昌，3300632.湖北航宇精工科技有限公司，襄阳，441000

0 引言

直升机的动力传动系统是其最重要的机械结构，直接关系着直升机的飞行寿命、机动性能和飞行安全。行星齿轮箱具有体积小、重量轻、传动比大、传动效率高与承载能力强等诸多优点，常常被用于直升机传动系统中。但重载、高速、高降速比、非封闭性等恶劣环境使得行星齿轮箱极易发生齿根裂纹、轮齿疲劳点蚀乃至轮齿或轴断裂等失效情况，影响直升机动力传动系统寿命，甚至导致飞行故障[1-2]。

相比横向振动信号，扭振信号从故障激励到传感器间的传递途径要简单得多，不容易受其他振源的影响，所以扭振信号的信噪比高，频谱成分也比横向振动信号更加简单。行星齿轮啮合位置会随时间变化[3]，但不会对扭振信号产生额外的调制作用，故扭振信号对故障更加敏感[4]。利用扭振信号更容易发现齿轮的点灼、胶合、齿根疲劳裂纹、局部断齿等早期故障，但相比横向振动，扭振信号更加难以采集。现有的很多测量方法或多或少地存在一些问题[5-7]。如现应用广泛的扭矩传感器：接触式应变扭矩传感器长时间工作后滑环易发热老化，甚至断裂脱落；非接触扭矩传感器由于算法和温度等因素影响，采集精度有待提高。编码器泛指各种以脉冲形式为输出信号的增量式编码装置，以及各种以脉冲法测量回转振动的传感装置。编码装置的输出信号都是连续的脉冲序列，相邻脉冲之间的时间间隔对应于被测轴转过一个角度增量的时间。编码器安装在旋转轴上，不破坏设备原有结构，用来精确检测旋转轴的位置，其较高的精度对分析扭振信号非常有利。增量式编码器有不同类型的形状和尺寸，可以适应不同的场合。

针对行星齿轮横向振动信号的特点，很多学者对其频谱结构、调频调幅特征进行了深入研究。MCFADDEN等[8]通过建立模型，研究发现行星齿轮箱横向振动信号的频谱有非对称性。INALPOLAT等[9-10]研究发现行星齿轮箱横向振动的边带结构的峰值通常在啮合频率周围，和行星轮的通过频率及其倍频有关。FENG等[11]对行星齿轮箱不同故障情况进行了深入分析，并建立了相应的响应信号表现形式。本文针对行星齿轮箱结构复杂和噪声混杂等特点，在综合考虑实际情况下，提出采用增量式编码器和高频脉冲计数的行星齿轮扭振信号测量方法。通过输入轴、输出轴扭振信号分析对比来说明以编码器采集的扭振信号在不同转速和不同负载下的特征。

1 扭振信号测试系统

1.1 增量编码器测量原理

假设采集卡时钟高频脉冲的频率为fc，编码器码盘上有Z个刻度，即编码器旋转一周将生成Z个脉冲。将增量式编码器与行星齿轮箱旋转轴通过弹性联轴器相连，将编码器输出的脉冲信号和内部晶振产生的高频时钟脉冲信号分别接在计数器的Gate端和Source端，连接方式如图1所示。

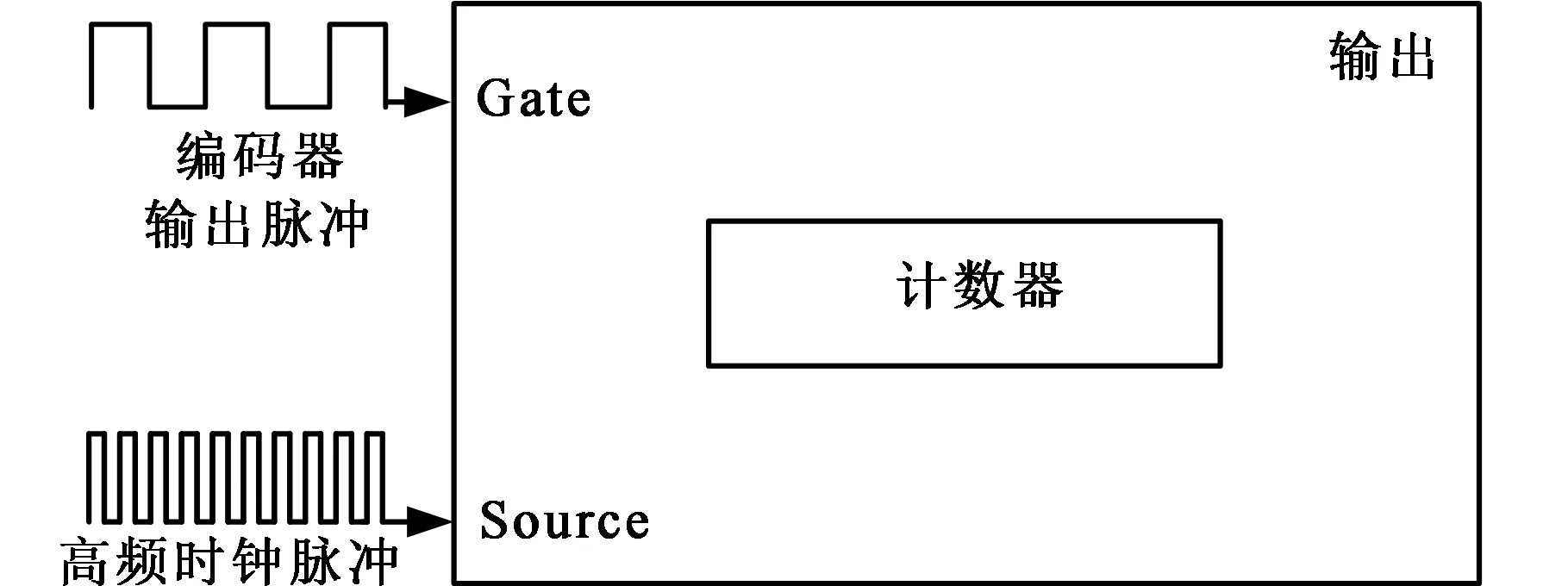
图1 信号连接方式Fig.1 Signal connection

计数器对Source端的高频时钟脉冲连续计数，编码器的输出脉冲每达到上升沿就触发计数器的锁存指令，锁存当前计数值并开始下一时刻的计数，并由计算机保存锁存的计数值。假设n为编码器转过一个刻度时的计数值，那么就可以得到一组计数器连续计数的计数值(n1,n2,…，nZ)，如图2所示。被测旋转轴每转一个编码器刻度的时间

T=nΔT=n/fc

(1)

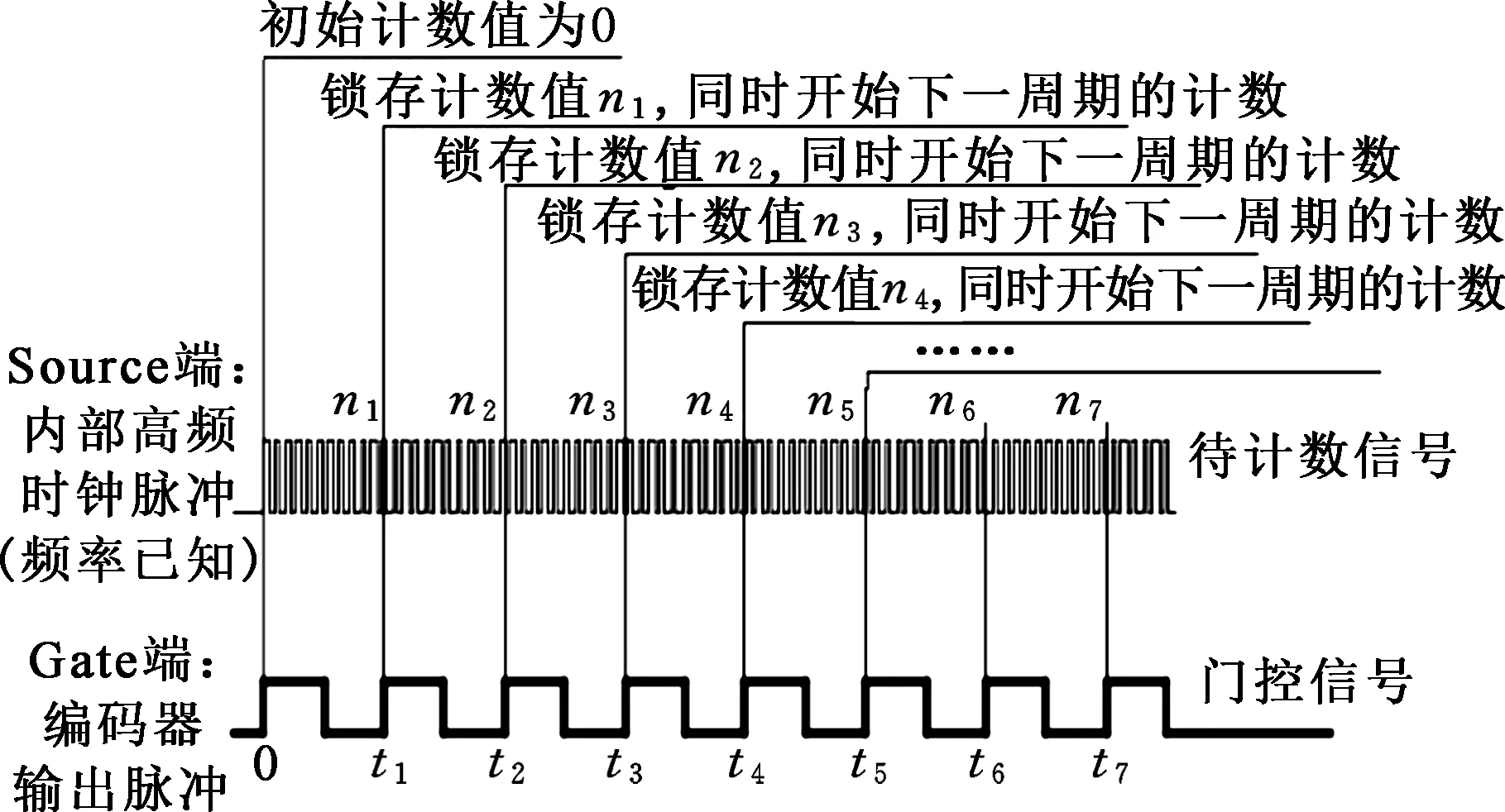
图2 扭振测量原理Fig.2 The measure theory of torsional vibration signal

增量编码器每转过一个刻度，旋转轴平均角速度

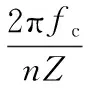
(2)

由于n≪fc，故可将平均角速度近似为瞬时角速度。

由此，可通过换算得到一组角速度向量和时间向量，分别为

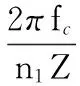
(3)

(4)

经过以上换算就可得到ω-t的角域信号，再利用线性插值重采样对角域信号重构，就可得到角速度形式的扭振信号，单位为(°)/s。

1.2 齿轮扭振实验系统

实验所用的行星齿轮箱为PXDS115-4型单级传动行星齿轮箱，行星齿轮箱相关的设备参数和运行参数如表1、表2所示。

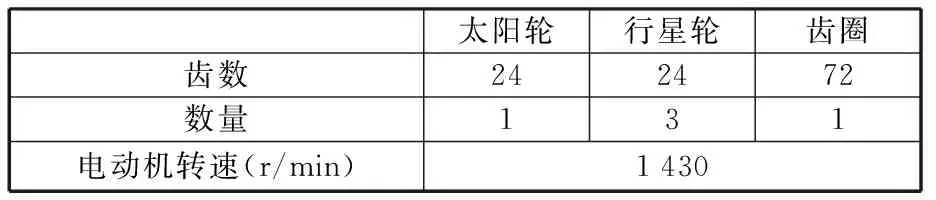
表1 行星齿轮箱设备参数Tab.1 The parameters of equipment

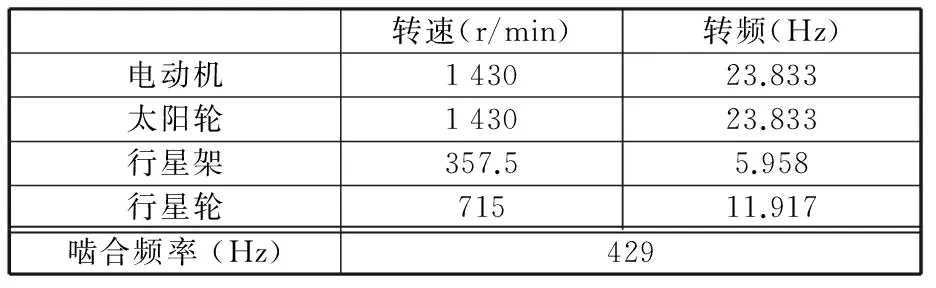
表2 行星齿轮箱相关运行参数Tab.2 Operating parameters about planetary gearboxes

根据相关公式计算[12]，行星轮局部故障频率fp=17.875 Hz。为了采集齿轮箱故障下的扭振信号，以人为破坏的方式对其中一个行星轮进行破坏，然后采用图3所示的实验平台采集行星齿轮箱扭振信号。

1.电动机 2.增量式编码器 3.联轴器 4.磁粉制动器 5.行星齿轮箱图3 实验平台Fig.3 Test platform

实验平台系统运行后将数据采集卡与增量式编码器相连，利用线性插值重采样的方法对角域信号重构，这样就得到了角速度形式的扭振信号。

1.3 扭振信号分析

行星齿轮箱一般由太阳轮、行星轮、齿圈和行星架等结构组成。一般情况下，齿圈固定不动，太阳轮绕自身的中心轴线旋转，行星轮既自转又围绕太阳轮公转。行星轮既和太阳轮啮合，又和齿圈啮合。当由加速度传感器采集横向振动信号时，由于行星轮的公转，各齿轮副的啮合点位置不断变化，时变的啮合点使振源与传感器的距离周期性变化，所以啮合振动经过时变传递路径的幅值调制传递给传感器，其调制频率为行星轮的公转频率。如图4所示，因为编码器安装在输入输出轴上，行星轮的啮合位置变化对采集的扭振信号没有调制作用。

图4 行星齿轮箱传动示意图Fig.4 Schematic diagram of planetary gearbox transmission

在行星齿轮箱的顶部和两侧分别安装加速度传感器以采集横向振动信号，图5所示为三个通道采集的横向振动信号频谱，图6所示为扭振信号的频谱。由两图可看出，在扭振信号的频谱中，太阳轮转频及其倍频、啮合频率及其倍频(二倍频、三倍频)的幅值很大，边频带也更加明显，更能有效地进行故障诊断。因为横向振动信号传递路径复杂，受到严重的噪声污染，信噪比低等原因，噪声会掩盖啮合频率及其倍频两侧边频带，边频带不易识别，难以进行有效的故障诊断，所以扭振信号相比横向振动信号，频谱结构更加简单。

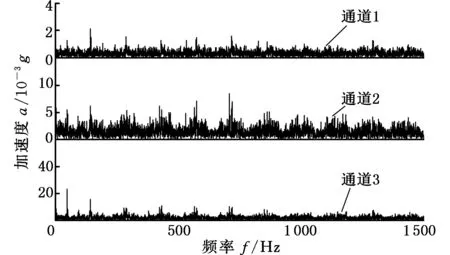
图5 横向振动信号频谱Fig.5 The transverse vibration signals spectrum

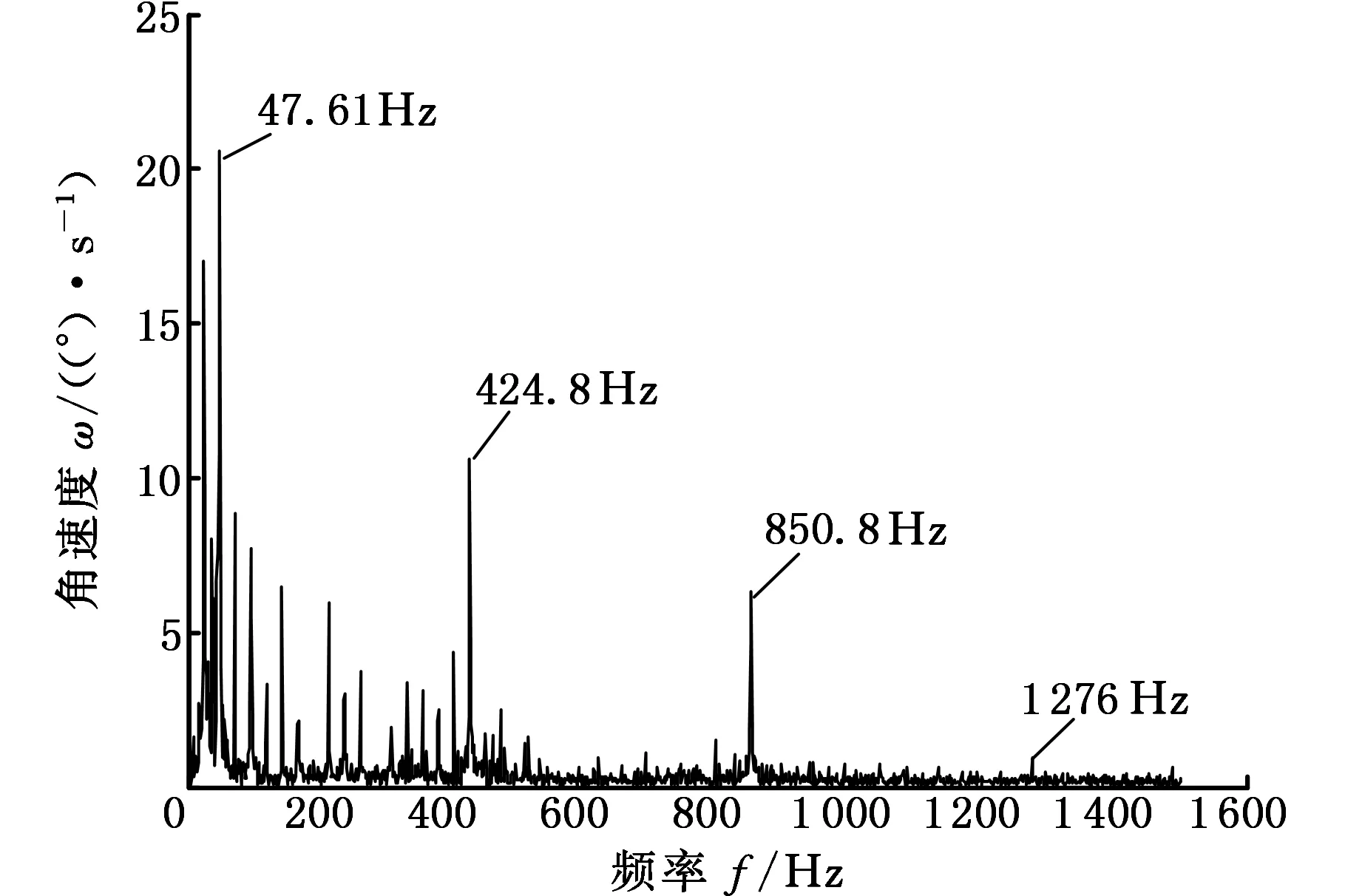
图6 扭振信号频谱Fig.6 The torsional vibration signals spectrum

2 行星齿轮箱输入输出轴扭振信号对比

因为编码器码盘的刻度固定，刻度之间距离相等,故当设备发生故障时，轴的转速发生变化，编码器产生的脉冲就会出现间隔疏密的变化，即计数值n1、n2、n3等是不同的，会随着转速变化而变化。由式(3)可得，当速度越快时，每转过一个刻度，连接在Source端的内部晶振所产生的脉冲数就越少，即n越小，相反，速度越慢n就越大。由式(4)可得，n越小，数据采集的时间间隔T就越短，分辨率越高，所包含的信息量越多。图7所示为不同转速下的扭振信号，所以采用编码器采集扭振信号时，应尽可能提高旋转轴的转速。

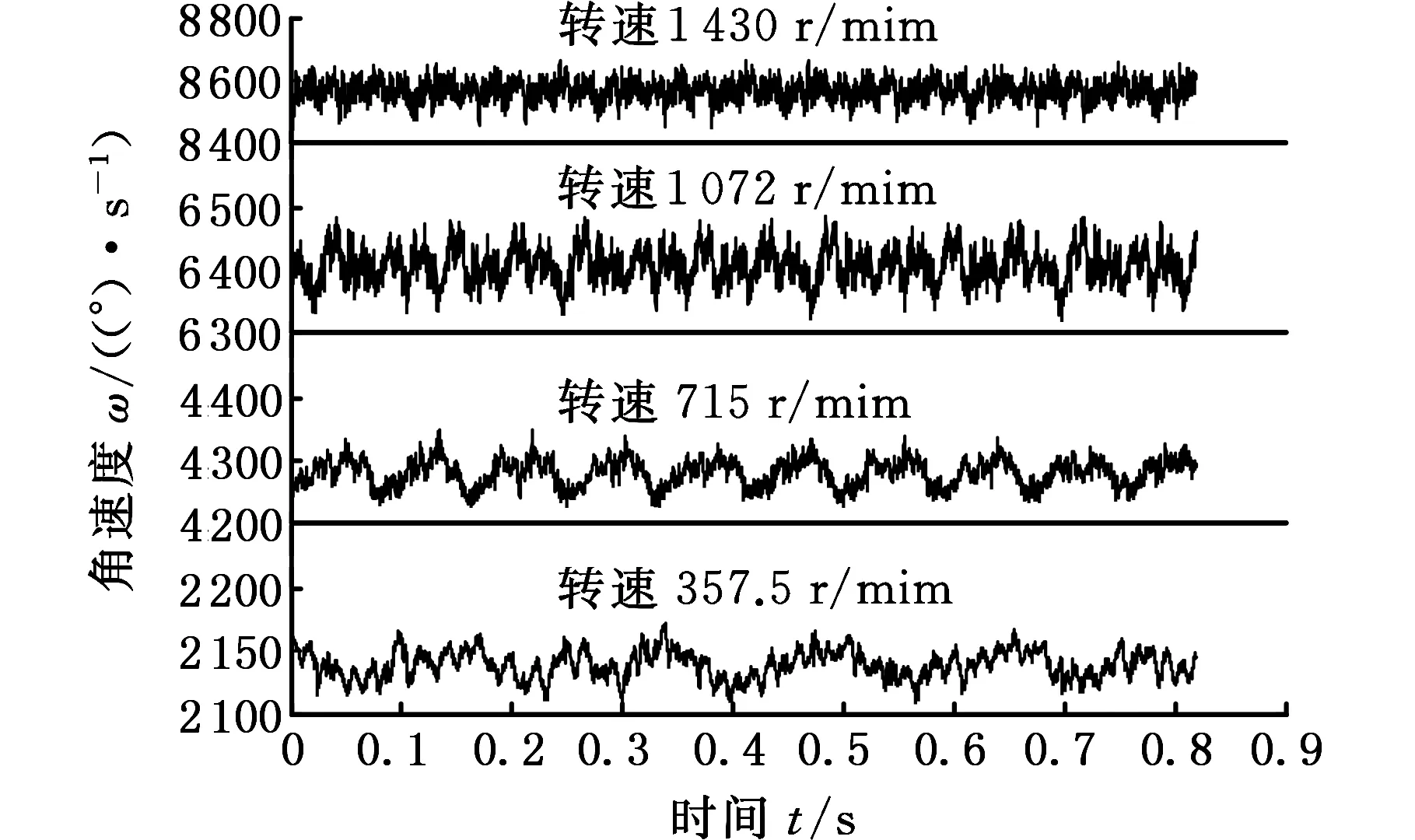
图7 不同转速下扭振信号Fig.7 Torsional vibration signals under different rotational speed

在图3所示的实验平台中，行星齿轮箱的输入输出轴都安装了增量式编码器。因行星齿轮箱的传动比为4∶1，故输入输出轴端增量式编码器的计数值n的比例为1∶4，则输入轴采集的信号分辨率更高，所包含的信息量更多。

2.1 正常状态输入输出轴扭振信号对比(实验状态1)

正常状态输入输出轴扭振信号及其频谱如图8、图9所示。其中，fm为啮合频率，fs为输入轴转频。由图9可看出，正常状态下采集的输出轴扭振信号的频谱图连啮合频率都不能凸显出来。相反，输入轴信号的频谱图则能很好地凸显转频、啮合频率和啮合频率的边频带。因为输出轴转速太低等原因，一般都是以输入轴的数据为分析对象。

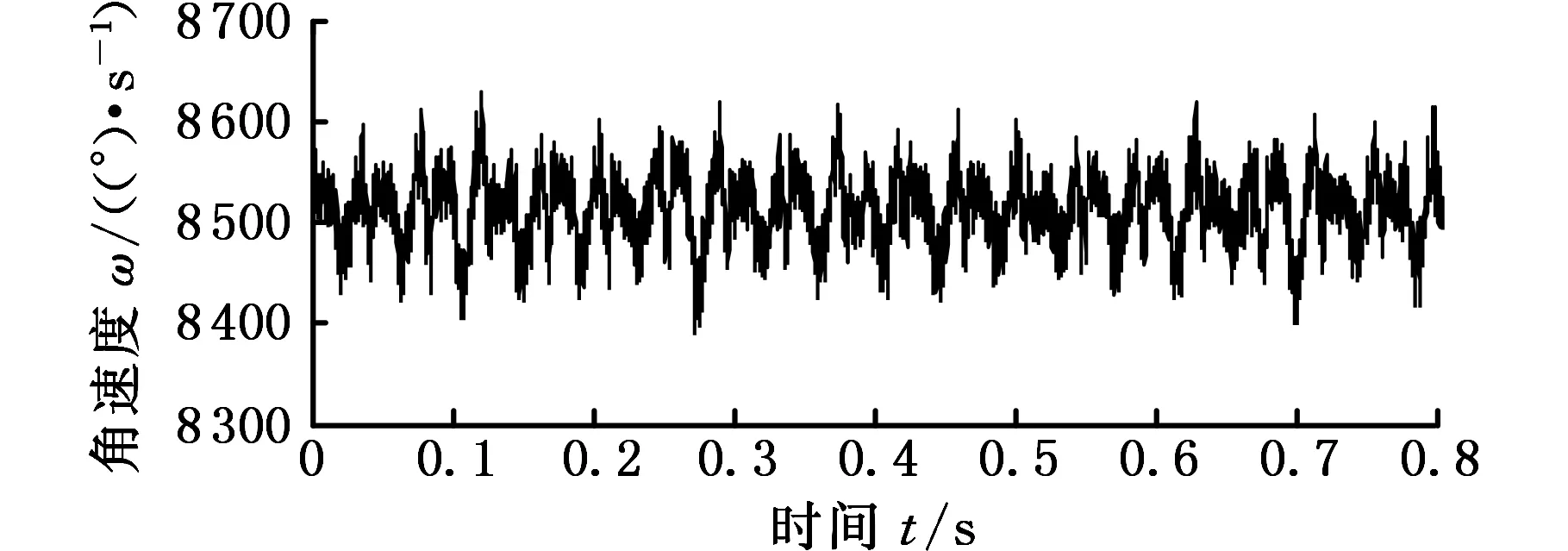
(a)输入轴采集的信号

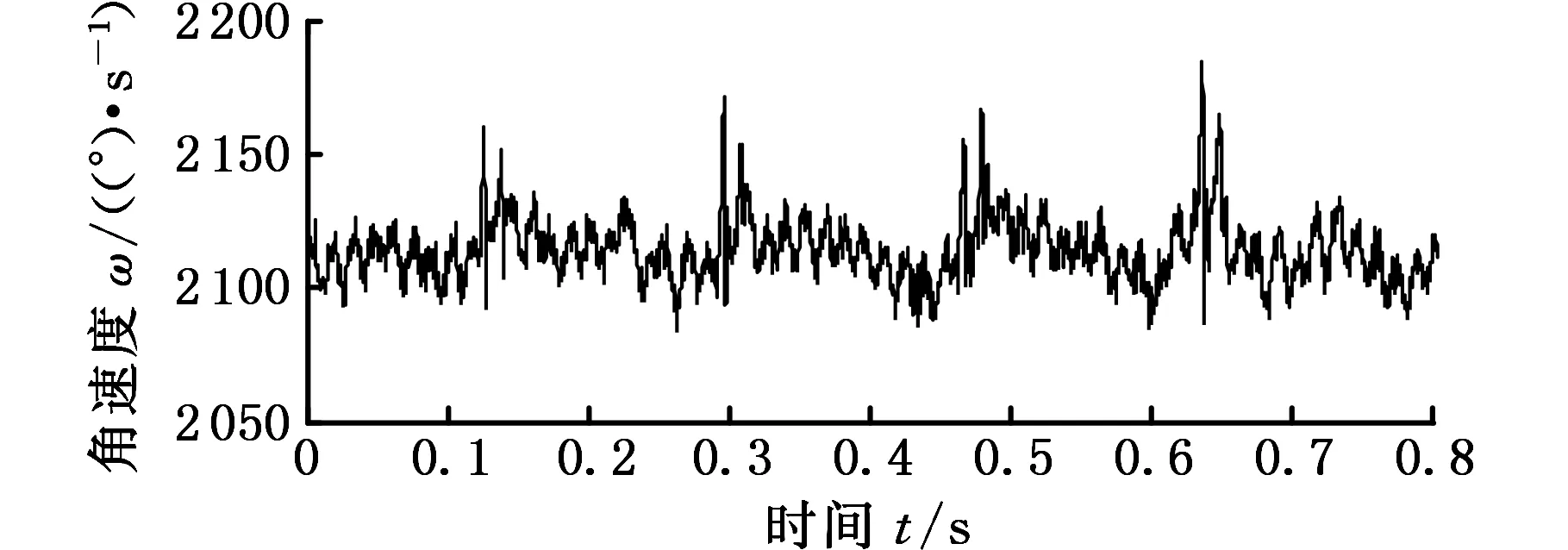
(b)输出轴采集的信号图8 正常状态下齿轮箱扭振信号Fig.8 Original two torsional vibration signals of gearbox with no failure

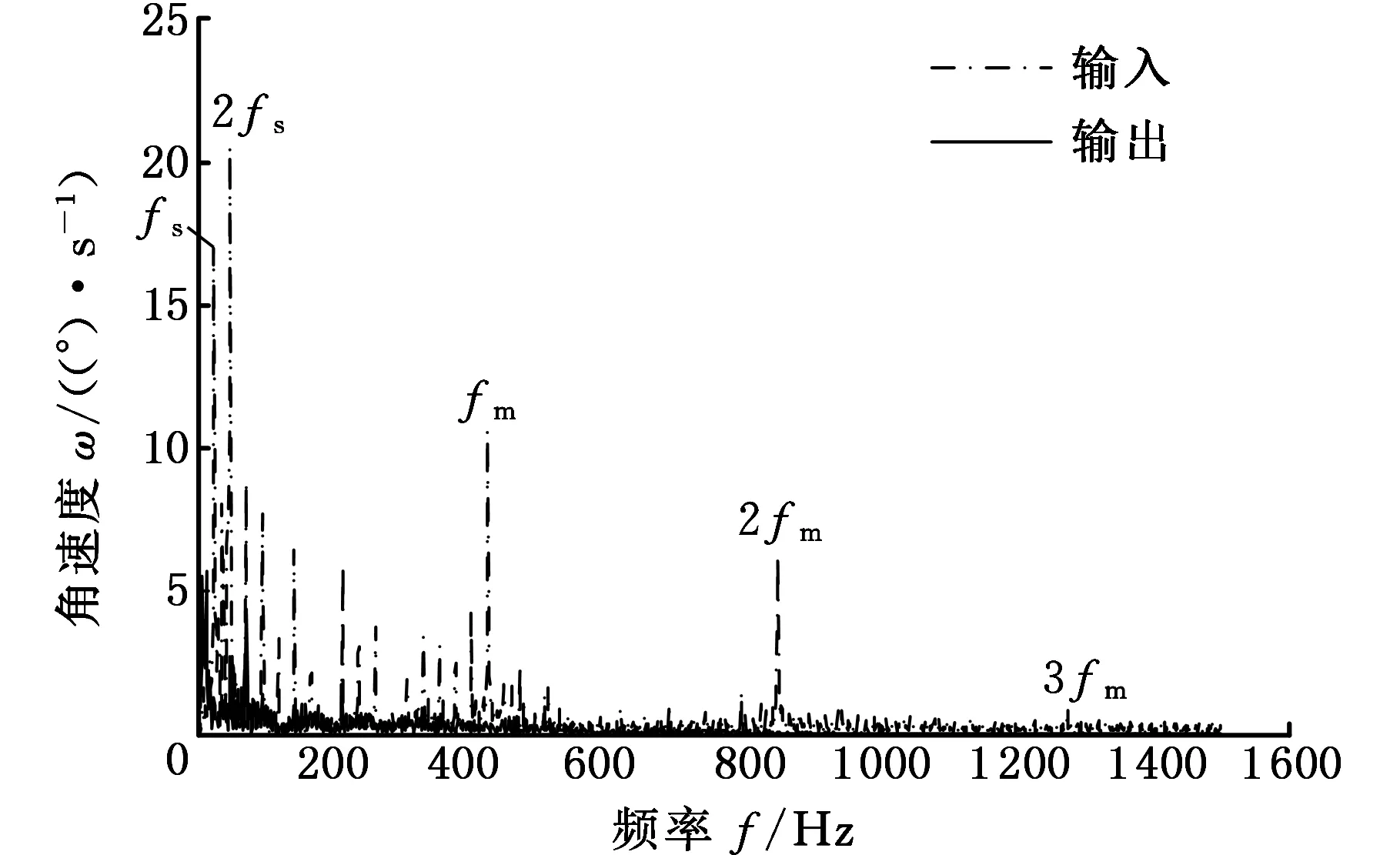
图9 正常状态下输入输出轴扭振信号频谱对比Fig.9 Comparison in spectrum between the two torsional vibration signals with no failure

由图8可看出，不管是输入轴还是输出轴都有周期性的冲击信号，分别为输入轴和输出轴的旋转周期。这是因为编码器安装在旋转轴上，通过测量旋转轴转速的波动来诊断是否有故障，所以所测旋转轴的转频在整个信号中所占的能量或比例就很大(作为主要载体)。即使输出轴信号的分辨率不高，也能在时域上明显看出旋转周期。但也正因这种特性，在很多情况下很难避免旋转轴的周期信号对判断故障冲击信号的影响；在频谱图中旋转轴的转频和啮合频率周围相应的边频带也十分明显，这也对频谱分析产生了一定的干扰。

2.2 一个断齿的输入轴和正常状态输入轴对比(实验状态2)

图10所示为故障状态下输入轴采集的扭振信号，图11所示为故障状态和正常状态的频谱对比。如图11所示，故障状态下的故障特征频率fp的幅值较正常行星齿轮箱有了很大程度的提高，在故障特征频率的倍频处(7fp-fj、8fp、9fp+fj)(fj为行星架转频)的幅值也有很明显的增幅，说明行星轮有破损。啮合频率及其倍频处(fm、2fm、3fm)幅值较正常行星齿轮箱也有明显增大，在频率为fm±nfp±kfj位置处(fm-3fp+fj、fm-2fp、fm-fp、fm+fp、fm+fp+fj等),出现明显的峰值，其幅值都大于正常信号(2fm处边频带则更加明显就不再标注)，而且这些峰值频率都和行星轮局部故障特征频率fp有关，这说明行星轮出现了破损。行星轮的局部故障会造成不均匀的行星架载荷分布，载荷不均匀会增强行星架旋转运动对啮合振动的调幅作用，使得频率为fm±kfj处的峰值都大于正常信号[13]。通过输入轴断齿和正常状态的频谱对比，可准确判断出行星轮的故障。

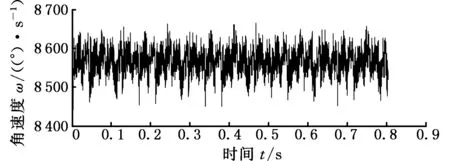
图10 输入轴采集的断齿状态下的扭振信号 Fig.10 Torsional vibration signals sampling location at input shaft with snaggletooth

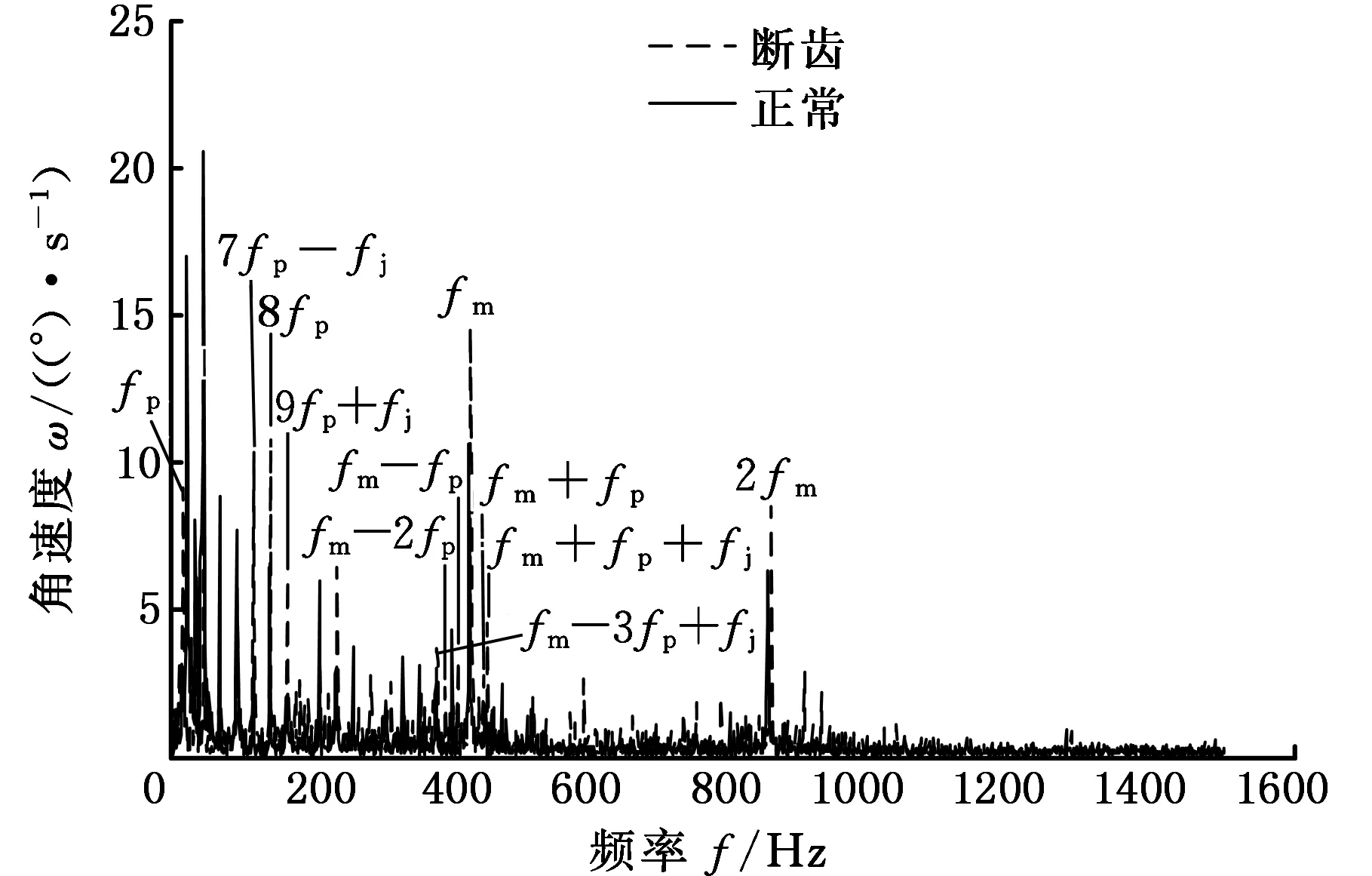
图11 两种状态下输入轴扭振信号频谱对比Fig.11 Comparison in spectrum between the two torsional vibration signals about input shaft

2.3 一个断齿的输出轴和正常状态输出轴对比(实验状态3)

图12所示为故障状态下输出轴采集的扭振信号，图13所示为故障状态和正常状态下的频谱对比。如图12所示，相比于正常状态，断齿状态输出轴的时域信号中冲击脉冲明显增加或混乱了很多，并且与图10输入轴信号相比，输出轴故障时在时域上的冲击特性更加明显。如图13所示，断齿状态下的频谱图也存在“类似”行星轮故障频率fp有关的边频带(fm-fp-fj、fm-fp、fm+fp、fm+fp+fj)。因为制造和安装误差的存在，即使行星齿轮箱没有故障它们也具有相应的分布式故障调制特征[14]，而正常状态下输出轴扭振信号的频率中不存在明显的啮合频率和故障边带，无法与输出轴故障信号进行准确对比，所以这组对比分析不能判断出行星轮的故障。

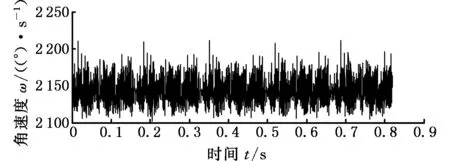
图12 采集的输出轴断齿状态下的扭振信号 Fig.12 Torsional vibration signals sampling locationat output shaft with snaggletooth

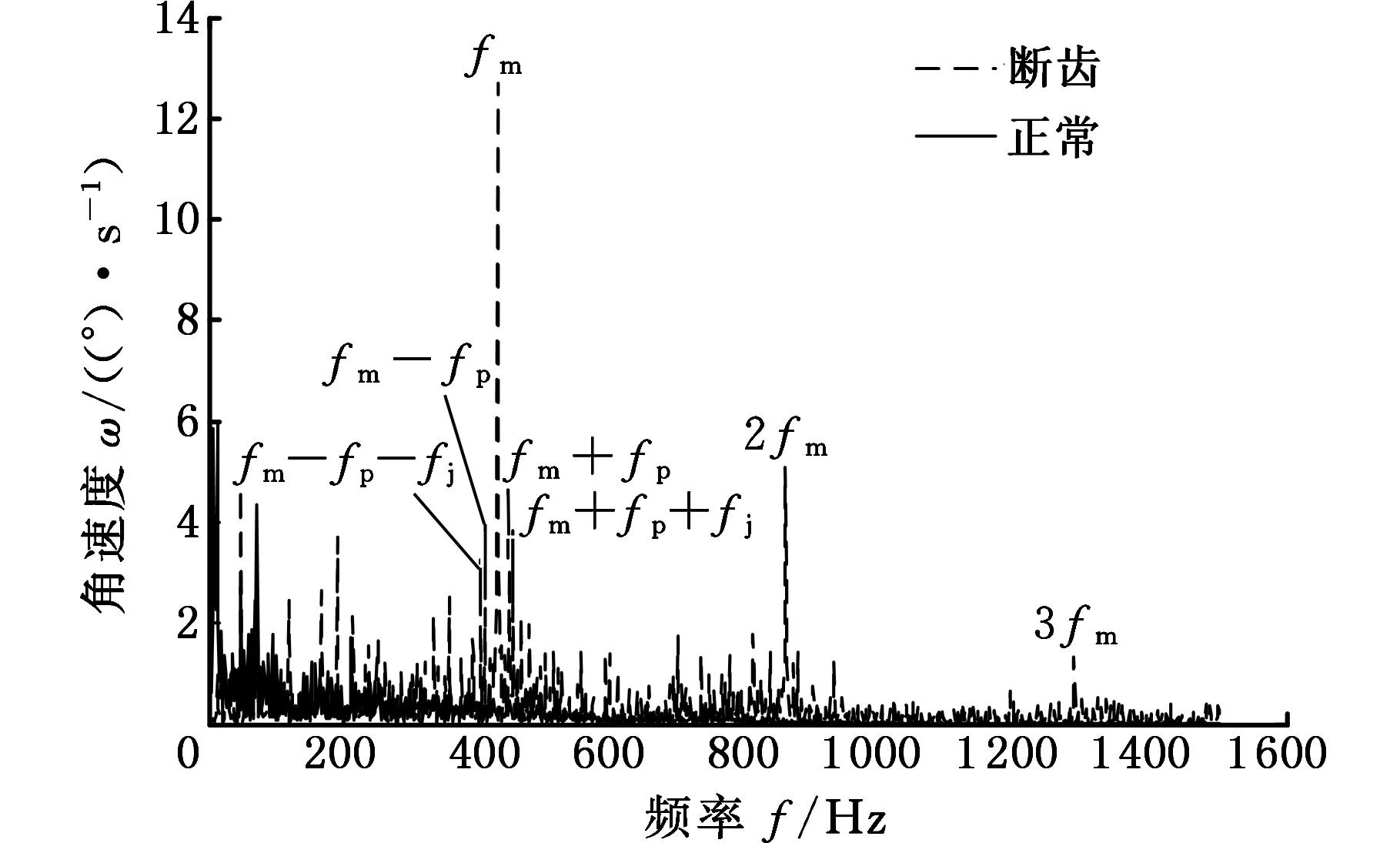
图13 两种状态下输出轴扭振信号频谱对比Fig.13 Comparison in spectrum between the twotorsional vibration signals about ouput shaft

2.4 一个断齿的输入轴和输出轴对比(实验状态4)

图14所示为断齿状态下输入输出轴信号频谱对比。其中，输入轴信号频谱中行星轮的故障特征更加明显，如故障频率fp，边频带fm-3fp+fj、fm-fp、fm+fp+fj、2fm-2fp、2fm-fp、2fm+fp等的幅值都大于输出轴相应频率，所以在一定转速下输入轴信号相比输出轴更能准确判断行星轮的故障。

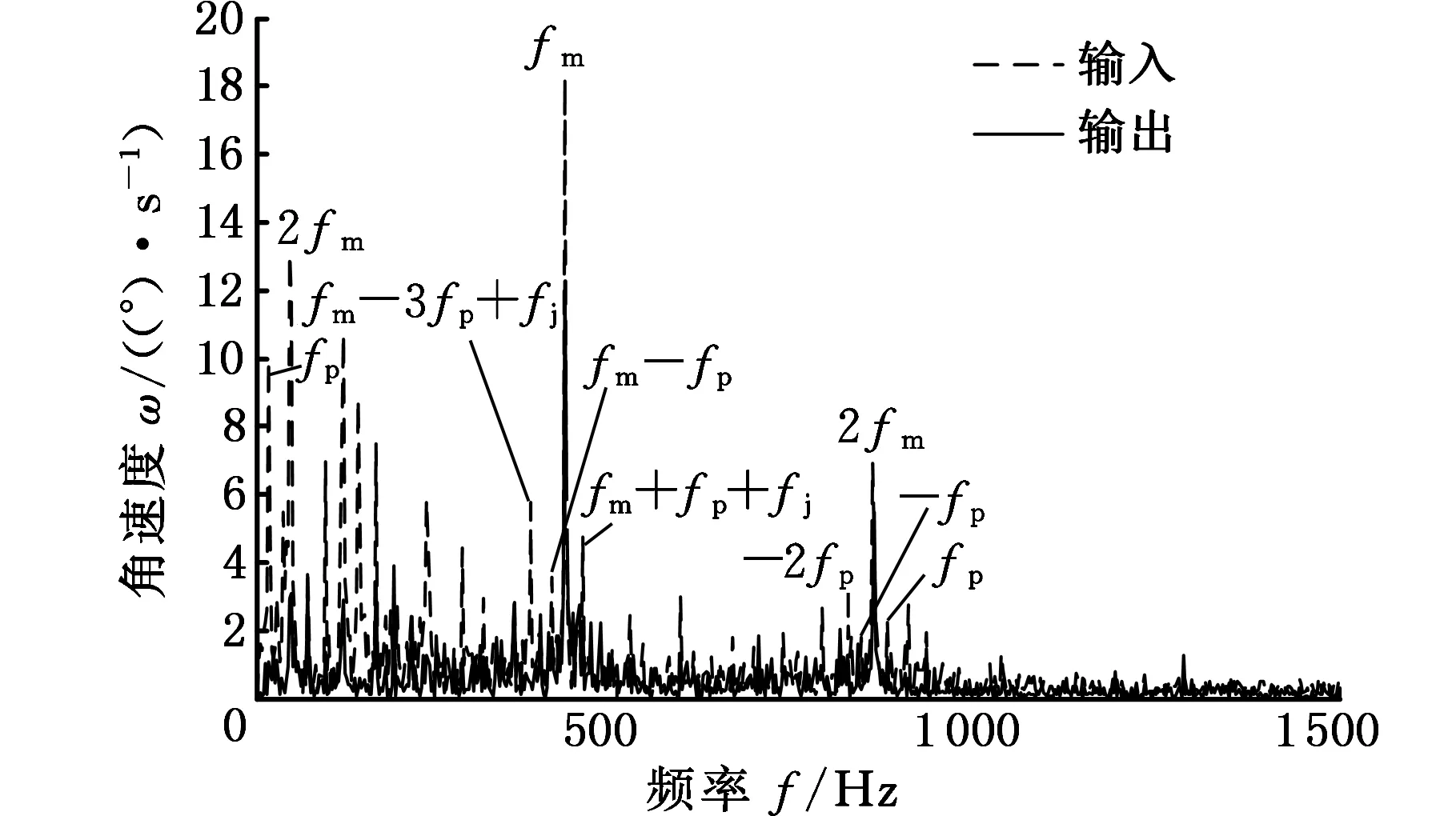
图14 断齿状态下输入输出轴扭振信号频谱对比Fig.14 Comparison in spectrum between the two torsional vibration signals with snaggletooth

通过4种情况的对比发现，在行星齿轮减速传动中，输入轴正常和故障状态下对比、故障状态下输入输出轴对比都能准确判断设备故障，将编码器置于高速轴上效果更好。若在输入输出轴两端同时安装编码器将使得硬件系统和软件系统更加复杂，成本预算也更高。表3为以上4种实验状态对应的结论。

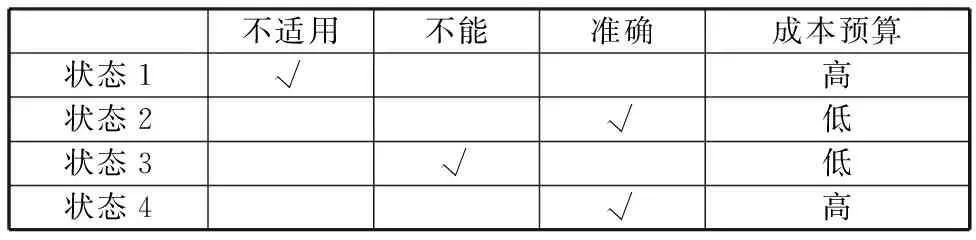
表3 4种实验状态判断故障准确性及成本预算Tab.3 The accuracy of fault diagnosis and cost budgeting

本次实验选用编码器每转产生2 048个脉冲，角度分辨率为360°/2 048=0.176°。以人工经验将旋转轴转速调试为340 r/min时，频谱如图15所示，啮合频率fm及其倍频、故障频率fp可以找到但不是很明显。当转速低于340 r/min时，就不能找出相应的故障特征，所以转速下限可设为340 r/min。编码器的精度越高，编码器的刻度数Z越大。由式(3)可知，当转速一定时，Z越大，计数值n就越小，所采集信号的时间间隔越短，所以精度越高的编码器，转速下限就越低。当精度足够高时，高速轴和低速轴信号之间的差距可被弥补。

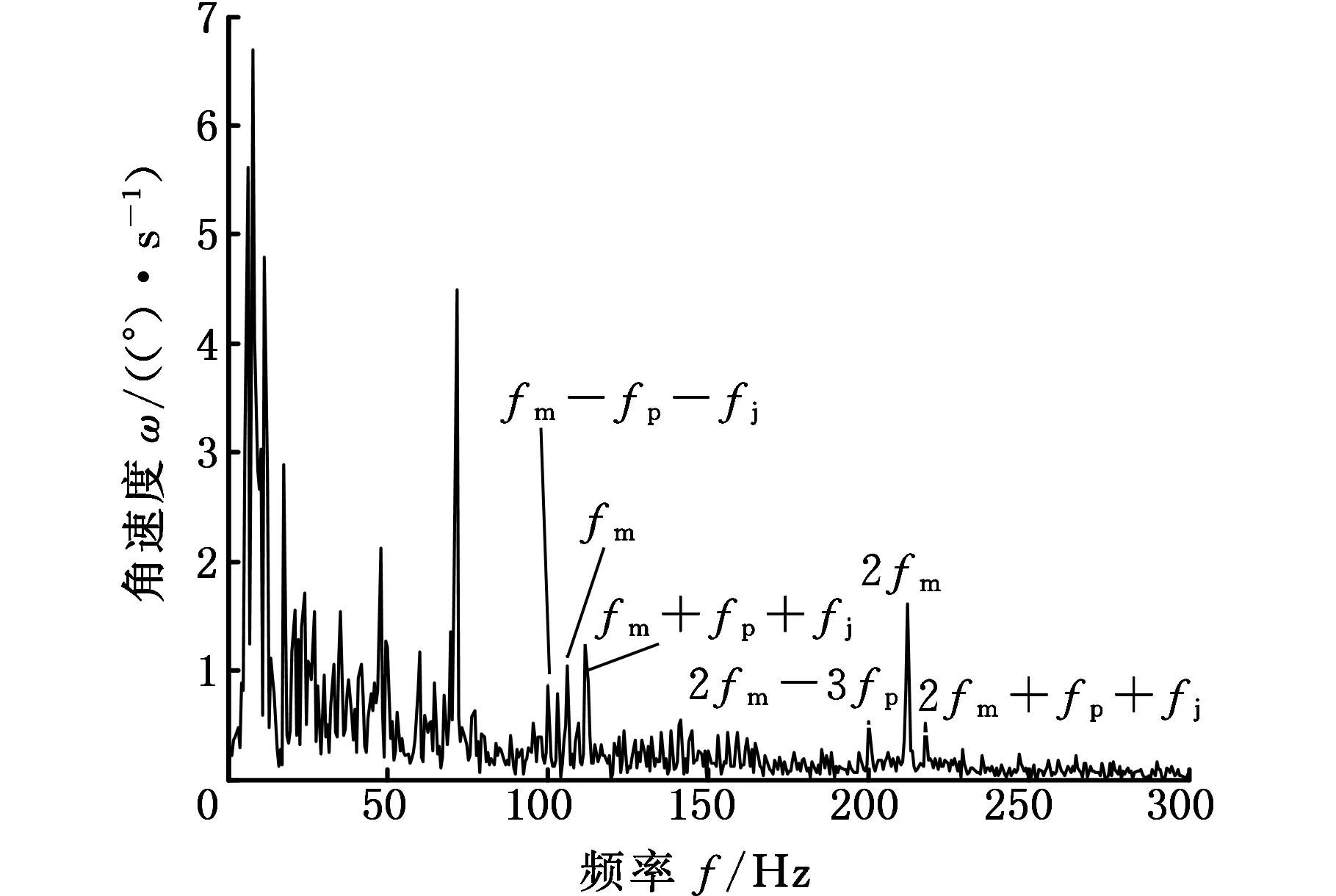
图15 转速340 r/min时频谱图Fig.15 Spectrum in 340 r/min revolving speed

3 大负载情况下输入输出轴信号对比

行星齿轮箱通常在恶劣环境下工作，为了更加接近行星齿轮箱实际工作状态，可通过磁粉制动器调节扭矩大小，增大负载。图16所示为负载增加到10 N·m时输入轴输出轴信号对比。相比于输入轴，输出轴的时域信号出现了特别明显的以T为周期的大脉冲。其中T=0.199-0.143=0.056 s，f=1/T=17.857 Hz，与行星齿轮故障频率fp相同，说明行星轮有故障，与实际情况相符合。表4所示为输入轴输出轴分别在正常状态和断齿状态的信号峭度值，再结合图8、图10、图12反映的情况来分析，发现行星轮出现故障后对输出轴信号的影响要更大一些。特别是在负载增加到10 N·m后，从输出轴的时域信号就可以判断出行星轮的故障。

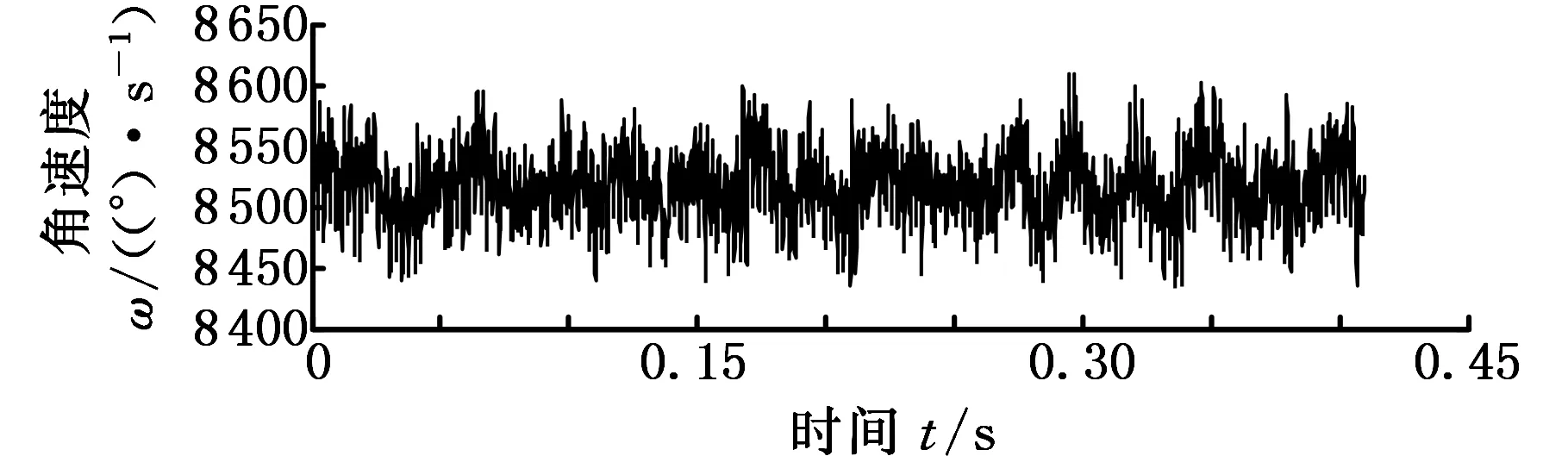
(a)输入轴

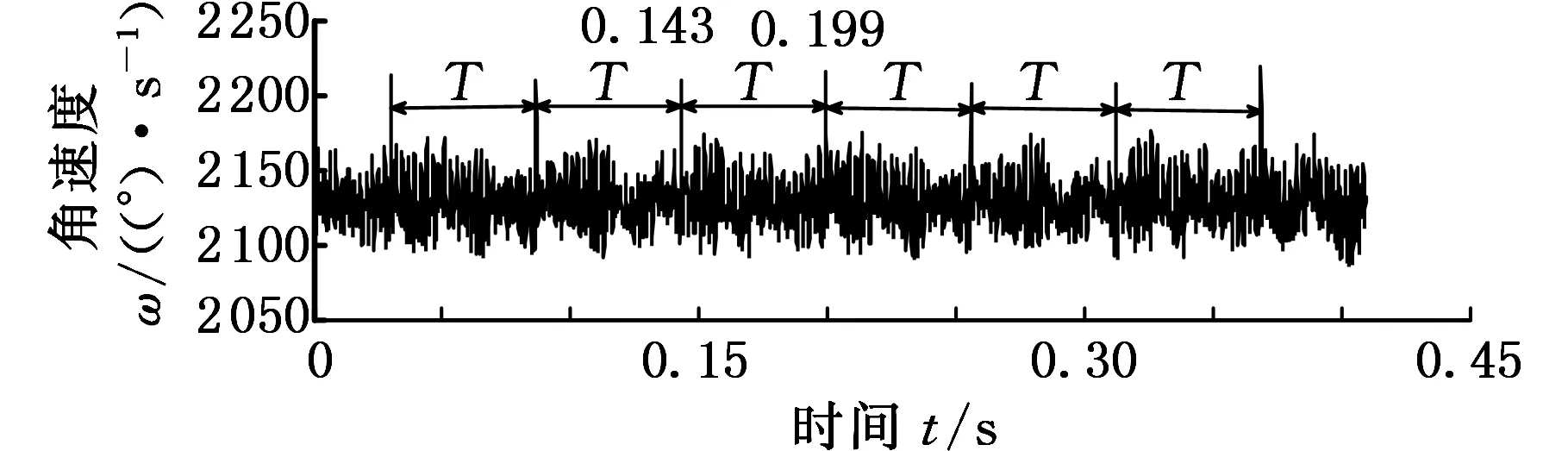
(b)输出轴图16 负载10 N·m输入输出轴信号对比Fig.16 Original two torsional vibration signals of gearbox in 10 N·m load

正常状态断齿状态输入轴3.00092.8205输出轴5.66092.8070

为了验证故障后系统所加的负载对输入轴输出轴采集的扭振信号的影响，再通过磁粉制动器将负载分别增加到20 N·m、30 N·m和40 N·m，输入轴、输出轴的信号分别如图17、图18所示。与负载10 N·m时相同，在负载为20 N·m、30 N·m和40 N·m时输出轴的时域信号出现了明显的以T为周期的脉冲，表5为各种负载下计算的周期T和频率f(因加了负载，测得的转速比理论值小，所以频率也不同)，所计算的频率f皆与相应行星轮故障频率fp相同。

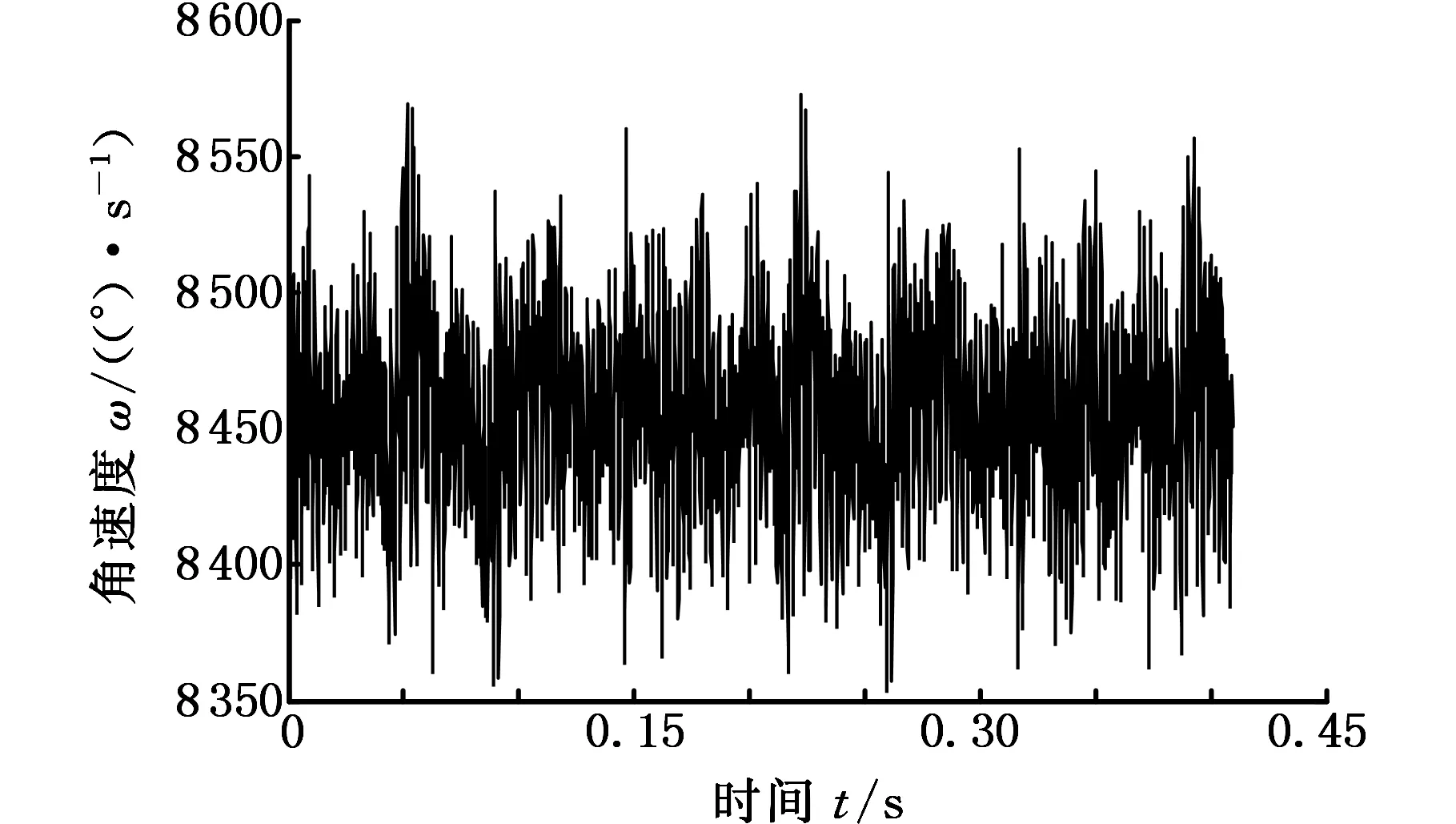
(a)20 N·m

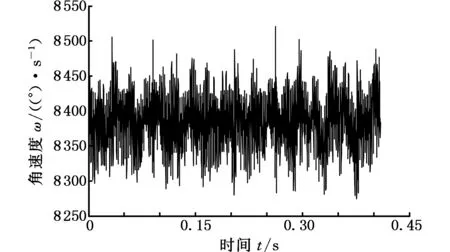
(b)30 N·m

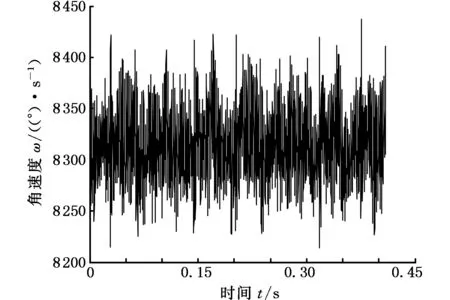
(c)40 N·m图17 不同负载下的输入轴扭振信号Fig.17 The torsional vibration signals sampling location at input shaft under the different loads

峭度指标是量纲一参数，对冲击信号很敏感，特别适用于诊断齿轮表面损伤类故障。峭度值越大表明信号中所含冲击成分越多。峭度指标定义为归一化的4阶中心距：

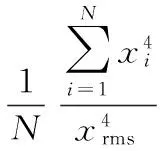
(5)

其中，峭度值

(6)

式中，xrms为x的均方根值；N为采样长度。

表6为故障状况时输入输出轴扭振信号在不同负载下的峭度值。随着负载的增加，输入轴基本保持不变，输出轴的峭度值越来越大，并且输出轴与输入轴峭度值的比例也越来越大。说明随着负载的增大，输出轴对故障冲击也越来越敏感，能准确清晰地“捕捉”故障信号。

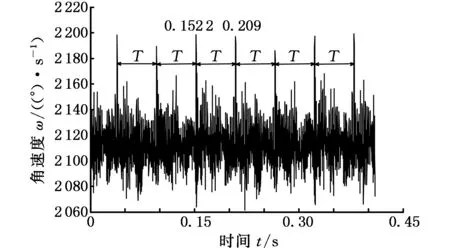
(a)20 N·m

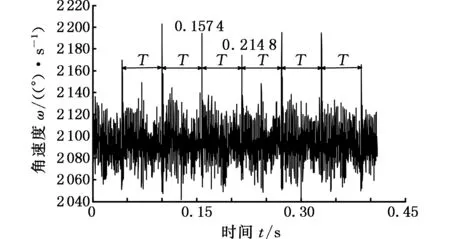
(b)30 N·m

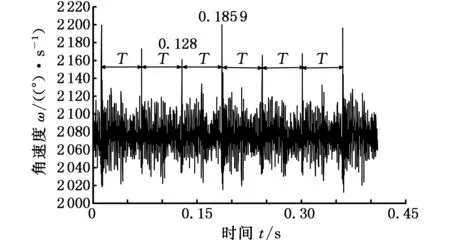
(c)40 N·m图18 不同负载下的输出轴扭振信号Fig.18 The torsional vibration signals sampling location at output shaft under the different loads

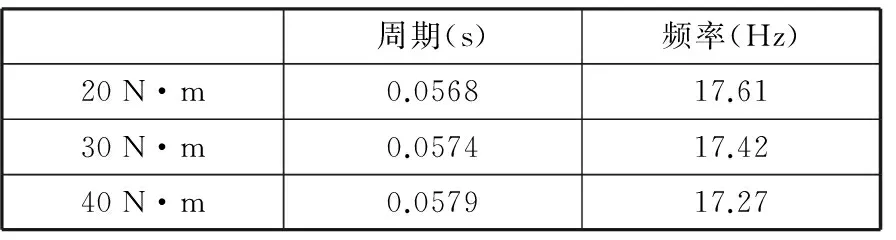
周期(s)频率(Hz)20N·m0.056817.6130N·m0.057417.4240N·m0.057917.27

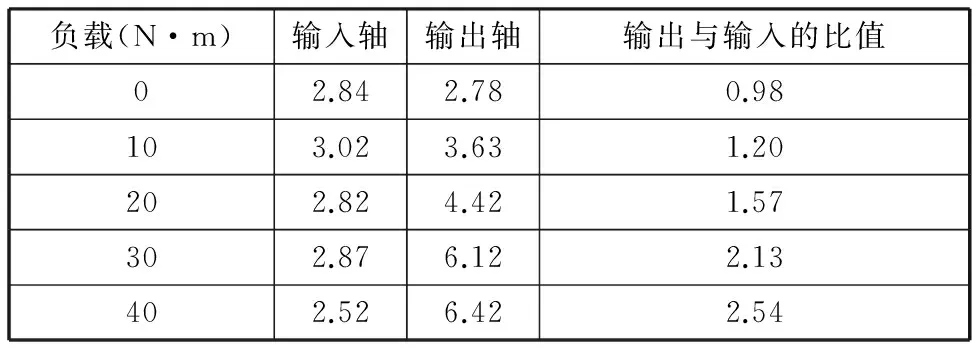
表6 输入输出轴扭振信号在不同负载下的峭度值

4 结论

(1)本文采用基于增量式编码器的扭振测量方法分别测量了输入轴和输出轴的扭振信号。编码器采集扭振信号时，转速越高,采集时间间隔越短，信号的分辨率越高，所以应尽量提高旋转轴转速。行星齿轮箱传动比大，减速传动中输入轴信号分辨率相对输出轴的要高得多。

(2)对输入输出轴正常状态和断齿状态的4种情况进行对比发现，通过比较正常状态和故障状态输入轴信号、以及比较故障状态下输入输出轴信号能对行星齿轮故障进行准确诊断，但前者的系统更加简单，成本也更低。

(3)即使输出轴信号分辨率偏低，但增大负载后，输出轴的时域信号能准确凸显故障冲击脉冲,并且通过峭度值对比，发现负载越大，输出轴对故障冲击就越敏感。诊断设备故障时,小负载情况下以输入轴信号为主，大负载情况下以输出轴信号为主。

[1] 陈康，刘建新.直升机结构与系统[M].北京：兵器工业出版社，2007：129-132.

CHEN Kang, LIU Jianxin. Helicopter Structure and System[M]. Beijing: The Publishing House of Ordnance Industry,2007:129-132.

[2] CHAARI F, FAKHAKH T, HADDAR M. Dynamic Analysis of a Planetary Gear Failure Caused by Tooth Pitting and Cracking[J]. Journal of Failure Analysis and Prevention,2006(2):73-78.

[3] 雷亚国，汤伟，孔德同,等.基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断[J].机械工程学报,2014,50(17)：61-68.

LEI Yaguo, TANG Wei, KONG Detong, et al. Vibration Signal Simulation and Fault Diagnosis of Planetary Gearboxes Based on Transmission Mechanism Analysis[J]. Journal of Mechanical Engineering,2014,50(17)：61-68.

[4] 丁康，李巍华，朱小勇.齿轮及齿轮箱故障诊断实用技术[M].北京：机械工业出版社,2005.

DING Kang, LI Weihua, ZHU Xiaoyong. Fault Diagnosis of Gear and Gearbox and Practical Technology[M]. Beijing: China Machine Press,2005.

[5] JANSSENS K, BRITTE L. Comparison of Torsional Vibration Measurement Techniques[M]// Advances in Condition Monitoring of Machinery in Non-stationary Operations. Berlin: Springer,2014:453-463.

[6] 张俊辉，罗银生，肖万猛.扭振测量方法及新型扭振测试系统研究[J].传感器世界，2012，18(12)：11-15.

ZHANG Junhui, LUO Yinsheng, XIAO Wangmeng. Torsional Vibration Measuring Methods and New Torsional Vibration Test System[J]. Sensorworld,2012,18(12):11-15.

[7] 孙良环.基于希尔伯特变换的扭振测量方法及其在齿轮故障诊断中的应用[D].太原:太原理工大学，2005.

SUN Lianghuan. Measuring Method of Torsional Vibration Based on Hilbert Transformation and Its Application in Gear Fault Diagnosis[D]. Taiyuan: Taiyuan University of Technology,2005.

[8] MCFADDEN P, SMITH J. An Explanation for the Asymmetry of the Modulation Sidebands about theTooth Meshing Frequency in Epicyclic Gear Vibration[J]. Proceedings of the Institution of Mechanical Engineers,1985,199(C1):65-70.

[9] INALPOLAT M, KAHRAMAN A. A Theoretical and Experimental Investigation of Modulation Sidebands of Planetary Gear Sets[J]. Journal of Sound and Vibration,2009,323(3/5):677-696.

[10] INALPOLAT M, KAHRAMAN A. A Dynamic Model to Predict Modulation Sidebands of a Planetary Gear Set Having Manufacturing Errors[J]. Journal of Sound and Vibration,2010,329(4):371-393.

[11] FENG Zhipeng, ZUO Migjian. Vibration Signal Models for Fault Diagnosis of Planetary Gearboxes [J]. Journal of Sound and Vibration,2012,331:4919-4939.

[12] FENG Zhipeng, ZUO Migjian. Fault Diagnosis of Planetary Gearboxes via Torsional Vibration Signal Analysis[J].Mechanical Systems and Signal Processing,2013,36(2):401-421.

[13] 冯志鹏,赵镭镭,褚福磊.行星齿轮箱齿轮故障诊断的幅值解调分析方法[J].中国电机工程学报,2013,33(8):107-111.

FENG Zhipeng, ZHAO Leilei, ZHU Fulei. Amplitude Demodulation Analysis for Fault Diagnosis of Planetary Geraboxes[J]. Proceedings of the CSEE,2013,33(8):107-111.

[14] 冯志鹏,褚福磊.行星齿轮箱齿轮分布式故障振动频谱特征[J].中国电机工程学报，2013，33(2)：118-125.

FENG Zhipeng, ZHU Fulei.Vibration Spectral Charactistics of Distributed Gear Fault of Planetary Gearboxes[J]. Proceedings of the CSEE,2013,33(2):118-125.