电磁场课程设计中新的数值计算方法探索

陈伟军，龙世瑜，刘如军

电磁场与电磁波是电子信息类专业本科生必修的一门专业基础课,该课程涵盖的内容是电子信息类专业本科阶段所应具备的知识结构的重要组成部分[1-2]。然而,该课程比较抽象、难以理解,并包含大量复杂的数学公式推导,尤为复杂的是电磁场的计算问题[3-4]。对于那些具有简单边界条件和场域几何形状规则的电磁场计算问题可以采用解析方法,对于多数复杂的电磁场问题的求解必须采用数值计算方法。本科教学中常介绍的电磁场数值计算方法有矩量法[5]、有限元法[6]和有限差分法[7-8]。

随着计算电磁学的快速发展,许多新的数值计算方法涌现,为本科阶段电磁场数值计算的教学带来了较大的挑战。本文介绍计算电磁学领域中一种新的无条件稳定的快速时域数值计算方法——基于加权Laguerre多项式(weighted laguerre polynomials,WLPs)的时域有限差分(finite-difference time-domain,FDTD)方法的基本原理及应用。把该方法引入到电磁场课程设计中,丰富和发展了学生对电磁场知识的理解,能有效提高学生的能力水平。

1 加权Laguerre多项式的正交性

定义如下Laguerre多项式[9-10]：

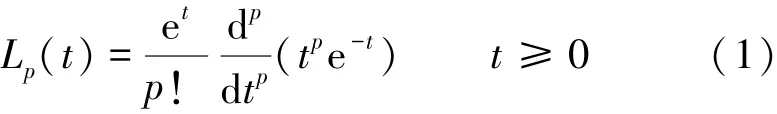
式中,Lp(t)是关于时间变量t≥0而阶数为p阶的Laguerre多项式。其满足加权函数e-t的正交性关系

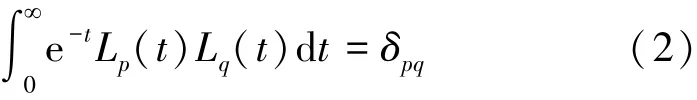
式中,δpq是Dirac函数。因此,根据式(2),可以获得一个正交基函数系 {φ0,φ1,φ2,…},

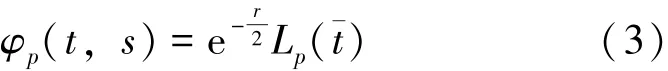
式中,¯t＝s·t,s是时间尺度因子。另外,Laguerre多项式具有以下的递推关系式：

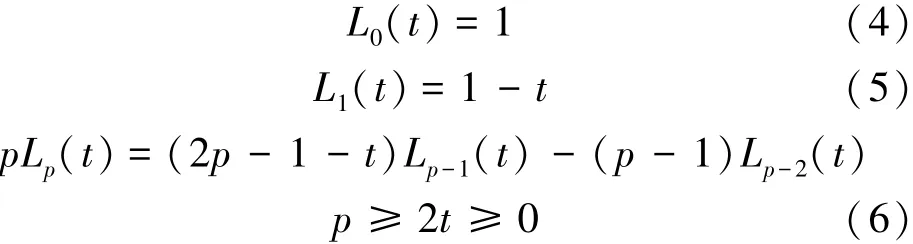
对Laguerre多项式的时间一阶求导,有：

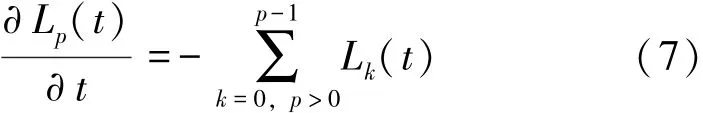
2 WLP-FDTD算法的公式体系

二维简单、无耗、均匀媒质中,TEz波的时域Maxwell方程表示为[11]：

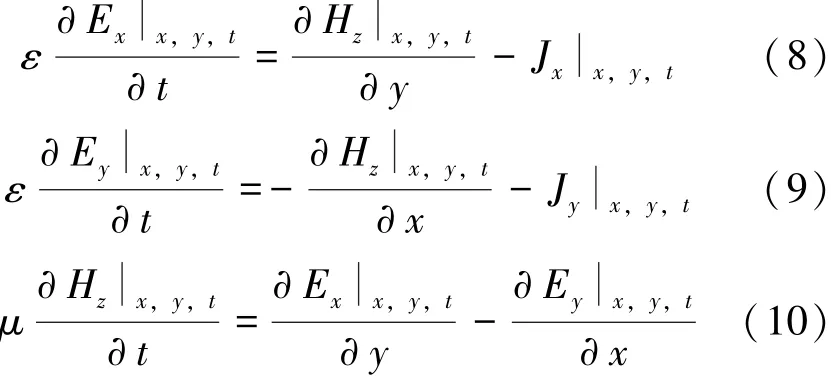
式中,ε表示介电常数,μ表示磁导率。使用加权Laguerre多项式作为时域基函数,式 (8) ～式(10)中的电场和磁场分量可以展开为[12]：

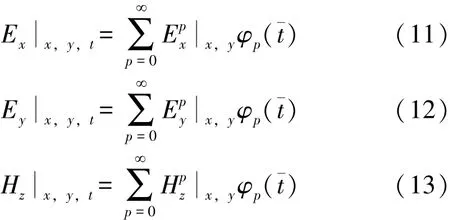
这样,原本是与时间和空间有关的电磁场分量变换成在与时间有关的函数和与空间有关的函数的乘积,有效地实现了时间和空间的分离。电场和磁场分量对时间的一阶偏导数为：

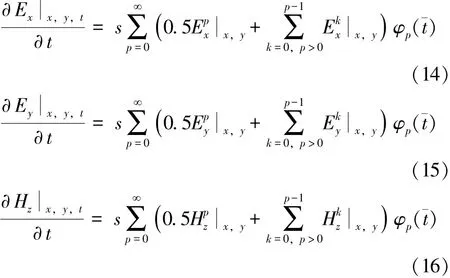
把式 (11)～式 (16)代入式 (8)～式 (10)中可以得到：

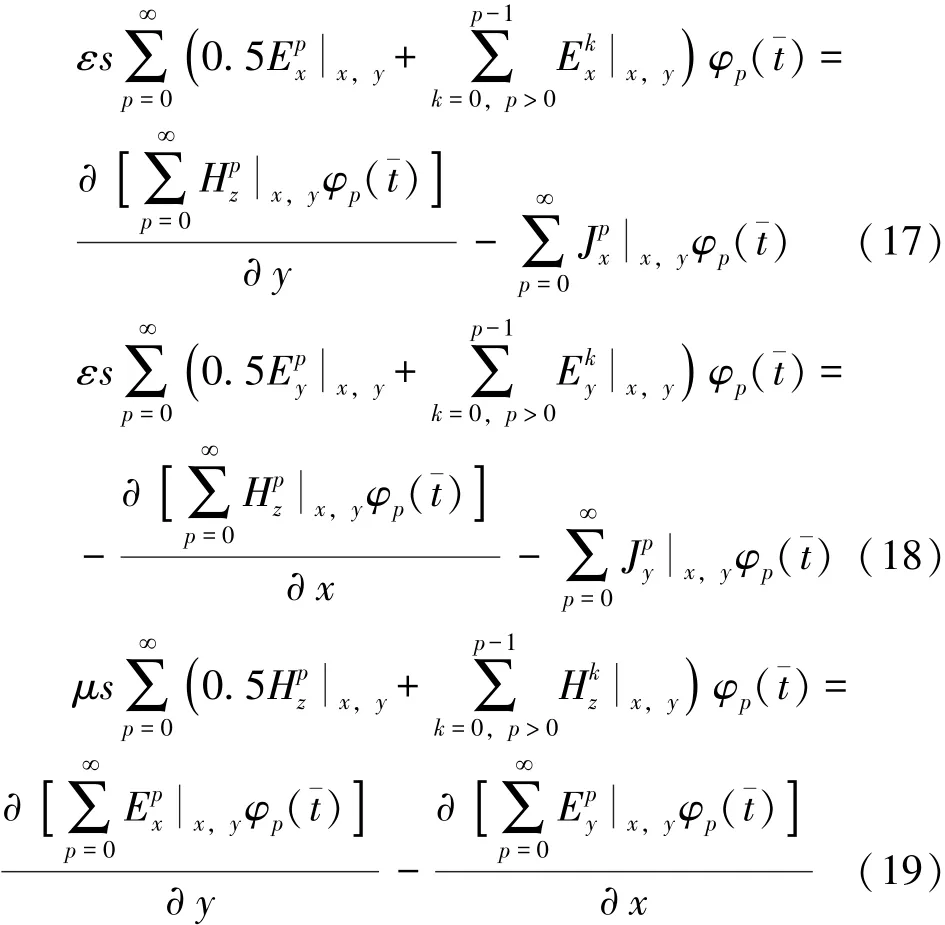
为了消除时间变量,利用Galerkin方法,在式 (17)～式 (19)两边同时乘以权函数φq(¯t),并在区间积分,可以得到：

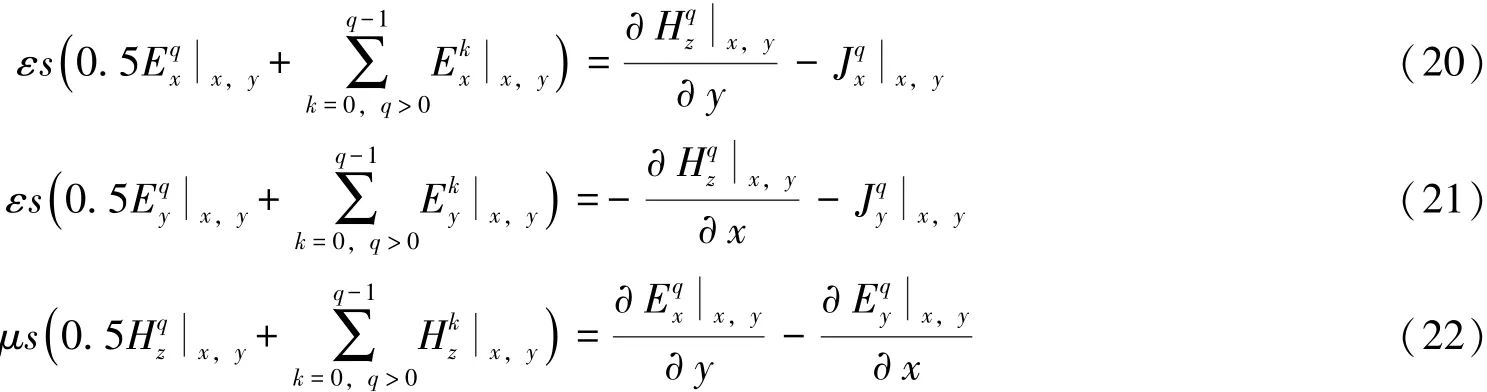
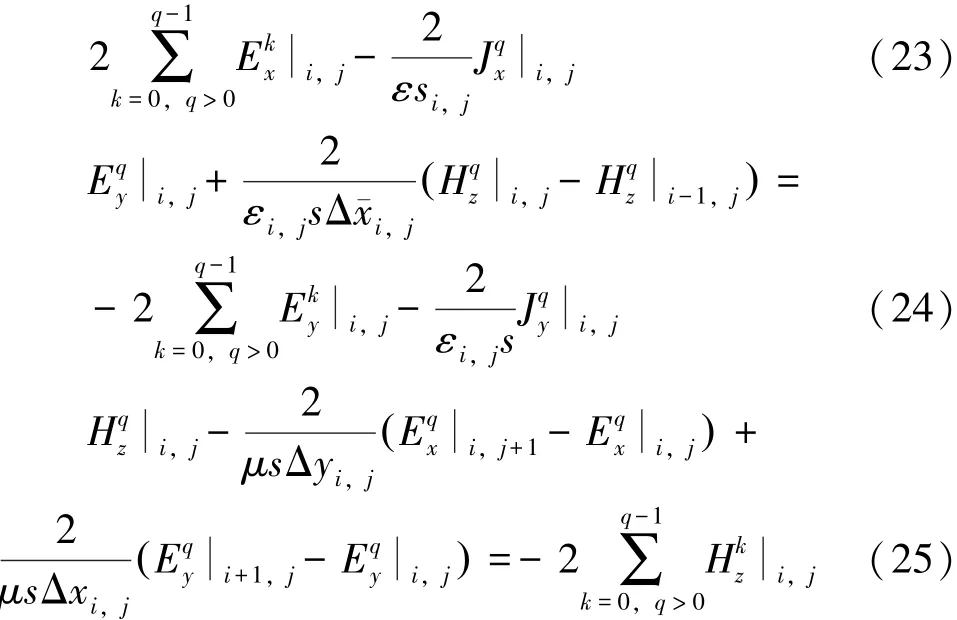
其中,Δxi,j,Δyi,j分别表示电场x分量和y分量所处网格的边的长度；Δ¯xi,j,Δ¯yi,j表示向量磁场位置之间的距离。二维TEz波的电磁场分布如图1所示。式(23)～式(25)中不包含时间变量,电场和磁场变量之间是隐式关系。为了求得电场和磁场变量,可以把式(23)～式(25)构造成矩阵方程：

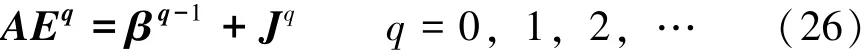
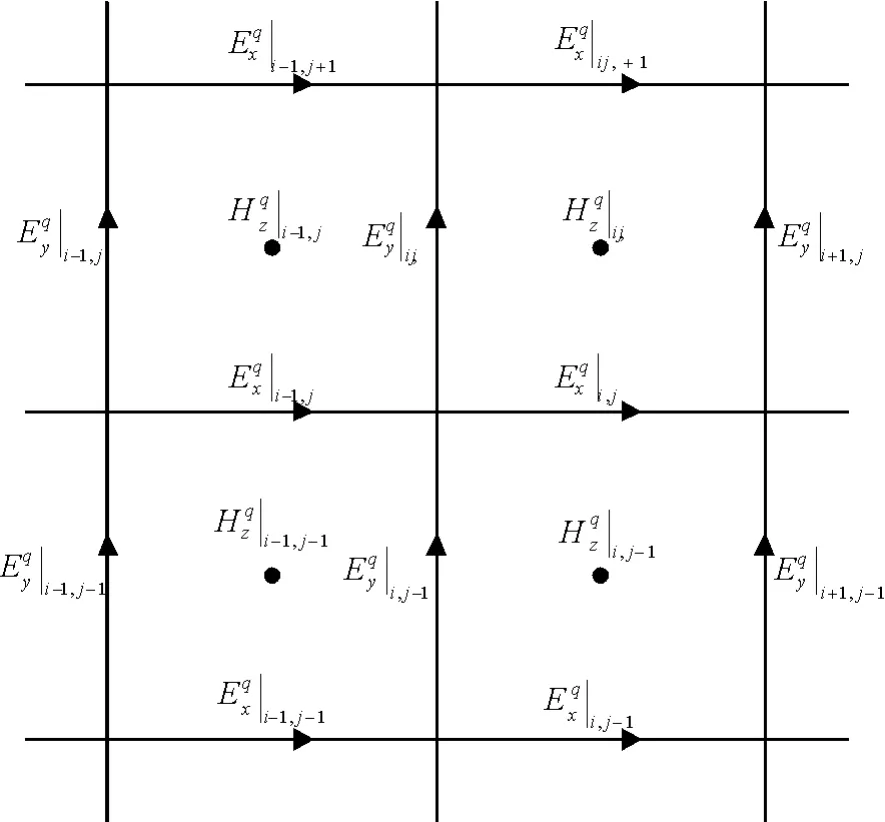
图1 TEz波瞬态电场和磁场分量在网格中的位置

其中,Eq＝ {Exq,Eyq,Ezq}T,Jq＝ {Jxq,Jyq,0}T,{βq-1}是与电场和磁场有关的0阶到q-1阶所有项的求和。WLP-FDTD算法中电场和磁场变量之间是成隐式关系的,并产生了一个大型稀疏系数矩阵A。这个系数矩阵A与加权Laguerre多项式的阶数无关,故式 (26)的求解可以仅对系数矩阵A只进行一次求逆或通过LU分解,然后按阶数步进求解。

通过按照阶数步进求解式 (26),每一阶时域基函数的系数可以计算出来,即电场和磁场的展开系数。从式(11)～式(13)可以得到时域电场和磁场分量的数值解：

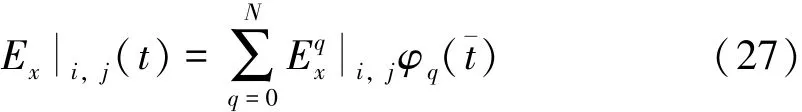
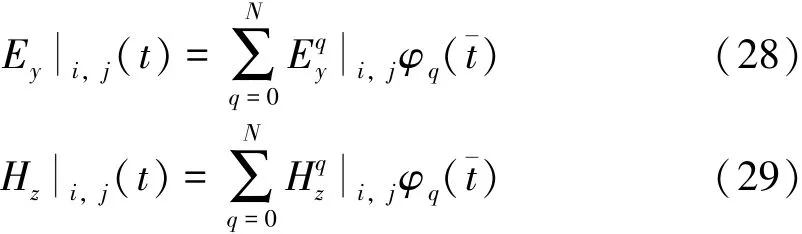
其中,N表示准确表征电场和磁场所需要的阶数。

3 仿真实例

考虑一个含有薄PEC挡板的二维平行板波导,如图2所示。为了模拟1μm厚的薄导体平板,在PEC挡板处沿电磁波传播方向划分为2个网格,网格的大小是0.5μm×0.005 m,计算空间采用了渐变网格,如图3所示,总的网格数量是120×12。由最小的网格尺寸,可以确定CFL时间稳定性条件Δt＝3.333 fs。WLP-FDTD方法中,计算数值积分所需的时间间隔取值为Δt＝4.0 ps。采用正弦调制高斯脉冲作为入射电流激励源,其表达式为：

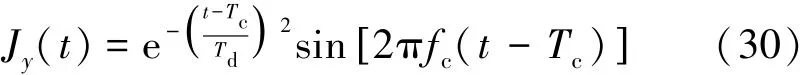
其中,Td＝1/2fc,Tc＝3Td。 我们选择 fc＝1 GHz,Tf＝11.71 ns,时间尺度因子s＝6.07×1010,步进阶数N＝150[13]。

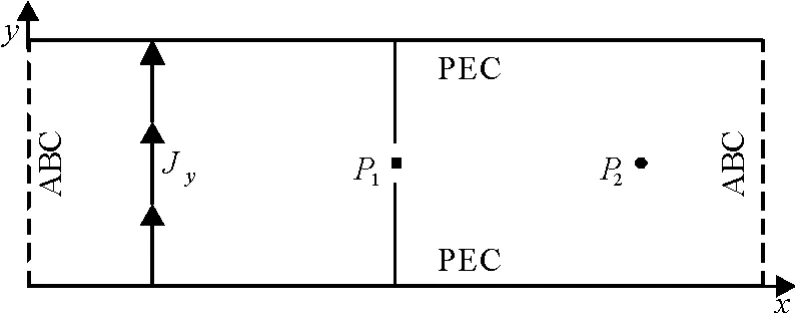
图2 包含有金属挡板的平行板波导

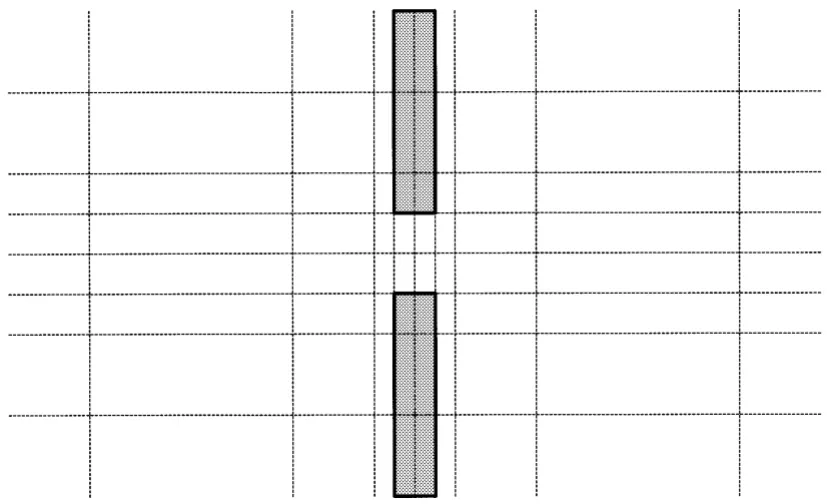
图3 金属挡板附近的渐变网格

如图4所示,表示在P1和P2点y方向的瞬态电场。WLP-FDTD算法和传统的FDTD算法计算的结果一致。如表1所示,给出了两种方法数值仿真的CPU计算时间和步进数目。由表1可以知道,WLP-FDTD方法仿真需要的步进阶数远小于传统的FDTD方法的时间步进数,其CPU时间只有传统的FDTD方法的15.5。本文所有的计算都是在配置为AMD Phenon II×6 2.80GHz 8 GRAM的计算机上进行。

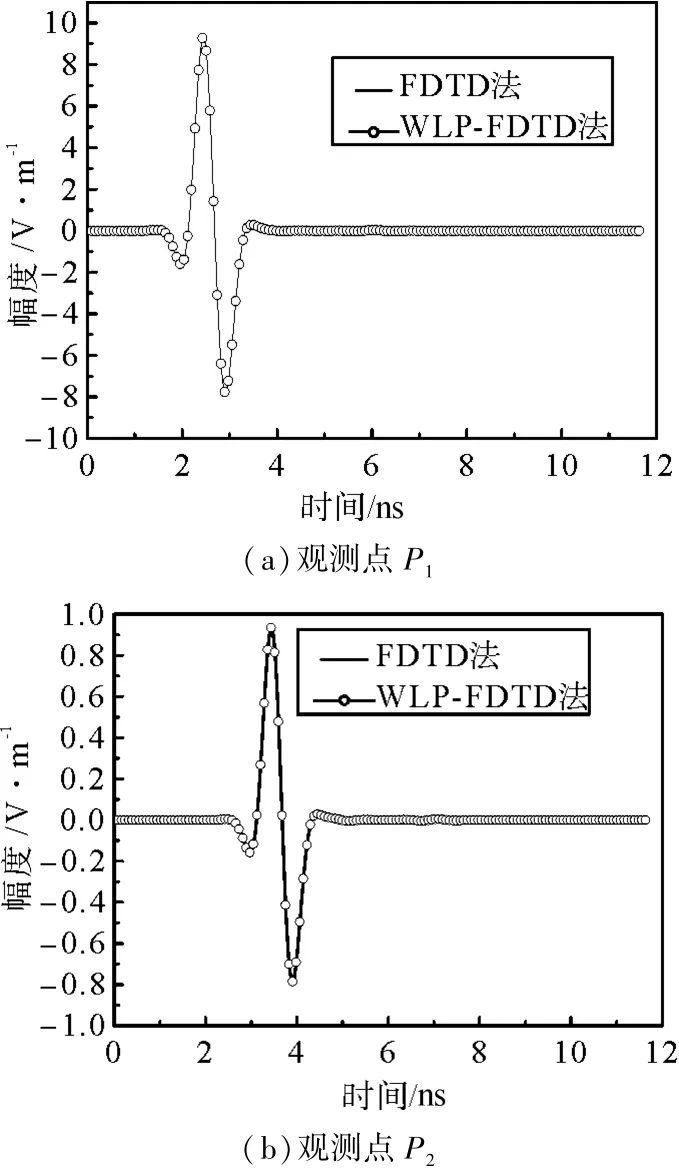
图4 电场Ey的时域波形图

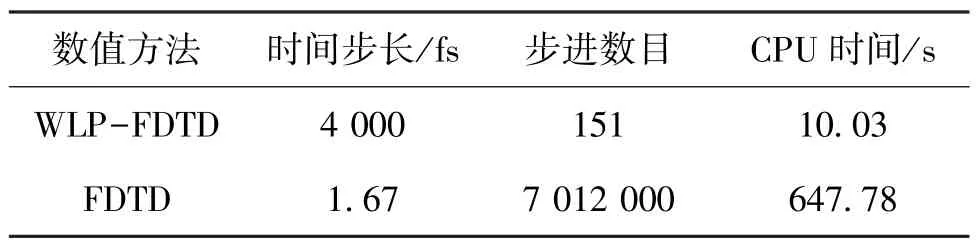
表1 带金属挡板的双导体平行板传输线效率比较

4 WLP-FDTD算法的难点

WLP-FDTD算法是电磁场领域的一种新的数值计算方法,公式复杂、难以理解,作为本科生电磁场与电磁波的课程设计有一定的难度。但是,能力较强的学生通过一段时间的努力后,能够比较顺利的完成,各方面的能力也得到较大的提高。根据学生完成该算法的情况,有几个关于该算法的难点需要关注。一是Laguerre多项式的数值实现方法；二是矩阵方程中系数矩阵的构建；三是根据电场和磁场的展开系数还原时域电场和时域磁场。学生可以通过查阅相关资料,相互讨论等方法解决以上3个难点,正确完成该算法。

5 结束语

本文主要介绍了加权Laguerre多项式的基本概念、正交特性及在此基础上推导了二维TEz波的WLP-FDTD算法的公式体系并用一个数值实验验证了WLP-FDTD方法的正确性和高效性。本文所表达的方法作为一种新的无条件稳定的快速时域算法可以作为本科电磁场课程设计,能有效帮助学生充分理解电磁场,提高学生对电磁场的知识水平,并对帮助本科生理解电磁场的数值计算具有一定的参考意义。

[1]谢处方,饶克谨.电磁场与电磁波[M].4版.北京：高等教育出版社,2006.

[2]邬春明.电磁场与电磁波[M].2版.北京：北京大学出版社,2012.

[3]王长清.现代计算电磁学基础[M].北京：北京大学出版社,2005.

[4]王长清,祝西里.电磁场计算中的时域有限差分法[M].2版.北京：北京大学出版社,2014.

[5]WALTON C,GIBSON.The method of moments in electromagnetics[M].Boca Raton：Chemical Rubber Company,2008.

[6]JIN J M.The finite element method in electromagnetics[M].Hoboken：John Wiley＆ Sons,2002.

[7]KARL S,KUNZ,RAYMOND J.The finite difference time domain method for electromagnetics[M].Boca Raton：Chemical Rubber Company,1993.

[8]SHENG X Q,SONG W.Essentials of eomputational electromagnetics[M].Singapore：Wiley-IEEE,2012.

[9]SHEN J,TANG T.Spectral and high-order methods with applications[M].Beijing：Science press,2006.

[10]SHEN J.Stable and efficient spectral methods in unbounded domains using Laguerre functions[J].Siam Journal on Numerical Analysis,2001,38(4)：1113.

[11]TAFLOVE A,HAGNESS S C.Computational electrodynamics：the finite-difference time-domain method[M].Boston：Artech House,2005.

[12]CHUNG Y S,SARKAR T K,JUNGB H,et al.An unconditionally stable scheme for the finite-difference timedomain method[J].Microwave Theory＆Techniques IEEE Transactions on,2003,51(3)：697-704.

[13]CHEN W J,SHAOW,LI JL,et al.Numerical dispersion analysis and key parameter selection in laguerre-FDTD method[J].IEEE Microwave and Wireless Components Letters,2013,23(12)：629-631.