系泊系统的优化设计模型

廖 青，张伟泉，吴 宁，王志勇

海洋蕴含着极为丰富的资源,如石油和天然气[1],目前我国的油气资源开发主要集中在近海水域[2]。系泊系统可以灵活观测、多参数测量海洋水文气象,浮标运动情况及锚系受力分析至关重要[3]。

目前对近海系泊系统的分析,国内外学者做了大量研究。文献[4-5]通过时域分析方法研究了系泊系统的动力特性。文献[6]采用数值方法分析了锚泊系统各链接点的受力状态。文献[7]中对单点系泊系统的外载荷进行了受力分析。

本文所研究的近浅海观测网传输节点由浮标系统、系泊系统和水声通信系统组成。浮标系统由一个圆柱浮标构成,系泊系统由钢管、钢桶、重物球、电焊锚链和锚组成。系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。

在设计时要求锚链末端与锚的连接处的切线方向与海床的夹角不超过16°,否则锚会被拖行,致使节点移位丢失。水声通信系统安装在密封钢桶里,钢桶竖直时系统的工作效率最高,钢桶倾斜角度超过5°,设备工作效果极差,重物球用于控制钢桶的倾斜角度。

1 问题假设

为简化研究问题,做出以下假设：

1)假设浮标和钢桶的重心在其几何中心；

2)假设海水密度均匀,不随深度的变化而改变；

3)假设浮标、钢管、钢桶、锚链和锚链接处均为各部件中心。

2 传输节点模型

传输节点中浮标系统由圆柱形浮标构成,系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。因为各部分间有拉力的作用,通过对每一个部分进行机理分析建立力学方程组,可以利用每一个部分间的相互拉力将其联系起来。

2.1 浮标受力分析

浮标虽然不沉不翻,但在风力和底部拉力的作用下,浮标并不会正立于水中,设浮标的倾斜角度为α,如图1所示,假设风力的方向平行于海平面,求出浮标在风向法平面的投影面积S。

考虑圆周的对称性,风力在竖直方向上的力矩相互抵消,浮标受到的风力在竖直方向上产生的总力矩为零,可通过积分计算垂直纸面向外的风力力矩分量,其和即为近海风载荷对浮标产生的总力矩M1。

图1 倾斜浮标

浮标在水下部分为一斜截圆柱体,根据其质心坐标(xc,yc,zc)可得到浮标所受浮力力矩M2。

浮标在水面上保持静止状态,根据牛顿第二定律对浮标建立力学平衡方程组；根据转动定理,浮标静止时,任何轴均可视作 “固定轴”,各力对该轴的力矩和为零,即可得力矩平衡方程：

式中：F1,F2,F3分别为近海风荷载、浮力、底部第一根钢管对浮标的拉力；β为拉力与水平面的夹角；G为浮标重力；M1,M2,M3分别为风荷载力矩、浮力力矩、拉力力矩。

2.2 四根钢管受力分析

4根钢管的受力分析类似,每根钢管受到重力、上下两根钢管的拉力和浮力。对第i根钢管,受力分析图如图2所示。

根据钢管处于静止状态,外力矢量和为零,建立关于钢管的受力平衡方程组。钢管处于静止状态,根据转动定理,钢管所受外力力矩和为零。类比式(1)得到每根钢管的力与力矩平衡力学方程组,本文不再赘述。

图2 钢管受力分析

2.3 钢桶受力分析

钢桶在水中处于静止状态,对钢桶进行受力分析,钢桶受到自身重力G、浮力Ffloat1、重力球拉力mg-Ffloat2、第四节钢管的拉力Fp1和锚链的拉力Fp2。受力分析图如图3所示。

图3 钢桶受力分析

根据钢桶处于静止状态外力矢量和为零,建立关于钢桶的受力平衡方程组。钢桶自身重力和浮力产生的力矩为零,钢桶处于静止状态,根据转动定理,钢桶所受外力力矩和为零。由此建立关于钢桶的力矩平衡方程,本文不再赘述。

2.4 锚链受力分析

锚链张力由两部分组成,一是锚链自身重力引起,二是由于约束浮标在波浪中的运动引起[8]。假设锚链均匀,在水中两端固定,取锚链长为βi的一小段分析[9-10],锚链受到头尾的拉力和自身的重力、浮力[11],如图4所示。

图4 锚链受力分析

在x,y方向锚链均受力平衡,根据相关悬链线知识给出关于锚线的悬链线方程[12]：

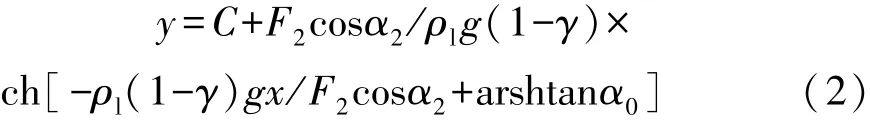
式中,ρl为锚链线密度,γ为海水密度与锚链线密度之比,F2表示这一小段锚链的尾所受到的拉力,α2表示该段锚链尾所受拉力与水平方向的夹角,C为常数。

考虑到锚链与锚连接端可能有部分锚链沉在海床上,设计中需考虑锚是否拖行问题,即需要对锚链与锚连接端是否部分沉底作出判断,若不满足海深约束,该型传输节点部分沉底。由于海水深18 m,锚始终放置于海床上则传输节点的竖直高度应该等于海水深,有：

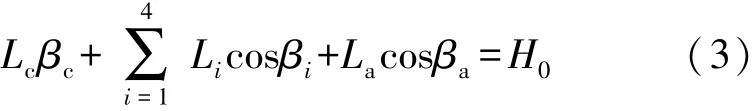
式中：Lc表示未沉到海床上锚链的有效长度,Li表示第i节钢管的长度,La表示钢桶的长度；βc表示锚链与其竖直方向的夹角,βi表示第i节钢管与其竖直方向的夹角,βa表示钢桶与其竖直方向的夹角；H0为海水深度。

由浮标的倾斜角度、水平切割面椭圆短轴端点到上表面圆边界的斜向距离、浮标所受底部第一节钢管对其的拉力大小和与水平面的夹角4个未知量将上述4个部分所有方程组联系起来,共同建立系泊系统传输节点模型。

按照建模顺序依次求解传输节点中各结构所处状态,包括钢桶钢管的倾斜角度、浮标吃水深度和游动区域。

3 系泊系统多目标优化模型

在传输模型基础上进行优化,将重物球的设计问题转化为多目标优化模型,通过改变重物球的质量使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。

3.1 多目标函数

钢桶的倾斜角度尽可能小,minβa。

3.2 约束条件

钢桶倾斜角度不超过5°。

锚与锚链连接点的切线方向与海床的夹角α0不得超过16°,否则锚会被拖行,致使节点移位丢失。

锚必须始终静止置于海床上,根据受力平衡,锚自身的重力要大于锚链对其的拉力在竖直方向上的分力与浮力之和。

式中,G表示锚的重力,F1表示锚所受的浮力,F0表示锚与锚链连接点处的拉力,

由此建立系泊系统设计的多目标优化模型。

浮标的吃水深度尽可能小,即水平切割面椭圆短轴端点到上表面圆边界的斜向距离h越大。

浮标的游动区域尽可能小,浮标的游动区域即为以浮标到锚的水平距离为半径的圆域,要使得浮标的游动区域尽可能小,即浮标到锚的水平距离尽可能小。

4 模型运用

为探究模型的可行性,针对一特定传输节点特定海域给出系泊系统设计方案。

某型传输节点选用Ⅱ型电焊锚链22.05 m,选用1 200 kg重物球质量。将该传输节点放置在水深18 m、海床平坦、海水密度为1.025×10-3kg/m的海域。

4.1 传输节点模型求解

1)12 m/s风速。

首先对锚链是否部分沉底做出假设,分别求出假设下的锚链状态。如图5所示,发现假设锚链与锚连接端未沉底时,整个传输节点已经不满足海深约束,所以该型传输节点部分沉底。

图5 锚链未沉底 (上)

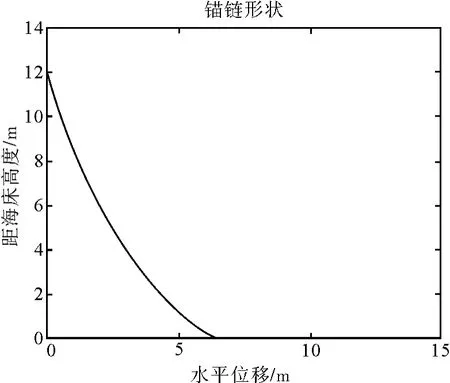
图6 锚链沉底 (下)

根据上述分析排除锚链未沉底的情况,如图6所示,考虑锚链与锚连接端部分沉底,显然满足锚链与锚连接端切线方向与水平方向夹角小于16°的要求。计算得到锚链沉底部分长7.95 m,进而计算钢桶和各节钢管的倾斜角度、浮标的吃水深度和游动区域。

2)24 m/s风速。

对锚链是否部分沉底进行判断,假设锚链未沉底,计算得到锚链的形状如图7所示。

图7 锚链未沉底图

计算结果表明,该假设下传输节点满足水深约束条件,锚链与锚连接处切线方向与水平夹角为11.810°,满足不超过16°设计要求,所以在风速24 m/s情况下,锚链未部分沉底,不需要再考虑假设二锚链部分沉底重复计算。

运用传输节点模型得到海面风速12 m/s下,钢桶的倾角为1.238°,第1根至第4根钢管倾角依次为1.195°,1.203°,1.211°和 1.212°, 浮标吃水深度为0.684 m,游动区域半径为14.573 m；在海面风速 24 m/s下,计算结果依次为 5.001°,4.826°,4.877°,4.909°,4.940°和 0.702 m,17.381 m。即为由传输节点模型给出的设计方案。

由上计算结果可知,钢桶倾斜角度已经达到临界值5°,即该型传输节点能够承受的最大风力为24 m/s,风力若进一步增大,该型传输节点的水声通信设备工作效率将变得极低。因此,若想进一步优化设计方案,可以改变重物球质量。

4.2 多目标优化模型

计算海面风速为36 m/s时,该传输节点的钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。

鉴于算法的复杂度,考虑对重物球的质量进行二次搜索,再使用距离权重法筛选。

例：在1 200～2 600 kg重物球质量中选择最优解。

1)大范围搜索。

设立步长为400,计算重物球质量从1 200 kg增至2 600 kg的结果,如表1所示。

表1 大范围搜索计算结果

从2 400 kg起,钢桶的倾斜小于5°,满足设计要求。

2)二次搜索。

对2 400 kg周围进行小范围的二次搜索,设置步长,寻求最优的结果,如表2所示。

表2 二次搜索计算结果

在2 400 kg左右重物球下,钢桶倾角和锚链与锚连接处切线方向与水平方向夹角均满足条件。

3)距离权重法。

设二次搜索后有n个重物球质量满足要求,第i个可行解得到的多目标函数中,浮标的游动区域半径为Ri,浮标吃水深度为hi,钢桶倾斜角度为βi。

定义第i个可行解的距离为：

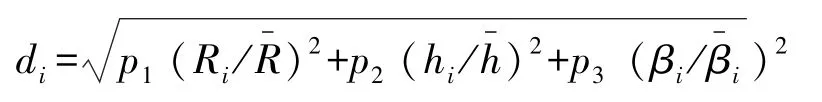
式中：p1,p2,p3为各目标函数的权重,可随机选取；R 是浮标平均游动区域半径；hi是浮标平均吃水深度；βi是钢桶平均倾斜角度。

随机取3组权重值计算可行解距离,如表3所示。

表3 3组权重赋值计算结果

3次求解结果表明重物球质量为2 450 kg为最终最优解。

5 结束语

本文对传输节点的每个组成部件都进行了受力分析,建立了关于力平衡与力矩平衡方程,使得每个组成部件彼此相互独立又有联系,使得模型的适用范围较广。但本文算法设计仍具有一定的误差性,需进一步改进。

[1]张火明.深海海洋平台混合模型试验技术研究与进展[J].中国海洋平台,2004,19(5)：1-6.

[2]袁梦.系泊系统动力分析[J].水动力学研究与进展,2010,25(3)：286-291.

[3]张继明.海洋资料浮标锚泊系统的系泊力计算[J].山东科学,2014,27(2)：20-24.

[4]KIM M H,TAHAR,KIM Y B.Variability of spar motion analysis various design methodologies/parameters[C]//Proceedings of the Twentieth Offshore Mechanics and Artic Enginering Conference.Newyork：OMAE,2001.

[5]KIM M H,KOO B J,MERCIER R M.Vessel/mooring/riser coupl-ed dynamic analysis of a turret-moored FPSO copmpared with OTRC experiment[J].Ocean Engineering,2005(32)：1780-1800.

[6]王道能.浮筒锚泊系统受力分析及其仿真[D].哈尔滨：哈尔滨工程大学,2008.

[7]余建星.风浪流联合作用下单点系泊船的受力分析[J].海洋技术,2005,24(3)：96-100.

[8]骆寒冰.规则波中浮标运动及锚链受力的实验研究[C]//第四届全国船舶与海洋工程学术会议论文集.镇江：中国造船工程协会,2009.

[9]钟于祥.锚泊船舶出链长度及张力估算[J].淮阴工学院学报,2004,13(3)：3-4.

[10]张养利.悬链线微分方程的另一种解法[J].第四军医大学学报,2001(1)：41.

[11]王丹,刘家新.一般状态下悬链线方程的应用[J].船舶工程,2017,36(3)：27-28.

[12]朱忠显.多成分悬链线锚泊系统的静力特性分析[J].大连海事大学学报,2015,41(4)：3-7.