基于受力分析的系泊系统优化模型
2018-01-15焦韩雪熊灿龙陈相蕾
焦韩雪, 熊灿龙, 陈相蕾, 张 勇
近浅海观测网的传输节点由浮标系统、系泊系统和水声通信系统组成,其中系泊系统的设计问题是海洋动力学中经常涉及的重要问题[1]。如何在海洋中尽量稳定地固定物体,是系泊系统设计时的关键。2016年全国大学生数学建模竞赛A题给出了某型传输节点的简化结构:其中浮标系统可简化为一圆柱体;系泊系统由钢管、钢桶、重物球、电焊锚链和抗拖移锚组成;水声通信系统安装在钢桶内。各部分组成的具体形状与重量等数据在题目及附件中给出。系泊系统的设计问题要求对于给定的环境,尝试确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度、浮标的游动区域及钢桶的倾斜角度均尽可能小。因此,系泊系统的设计问题可以归结为多目标的优化问题。近浅海观测网中采用的系泊系统属于单点单浮筒多成分的系泊系统。在进行该系泊系统的设计时,需要考虑的主要环境因素有风速、水流速度、水深3方面。本文以2016年全国大学生数学建模竞赛A题中的系泊系统为研究对象,结合题目所给定的环境条件,进行受力分析,得出了不同情况下系泊系统的最优设计方案。
1 基本假设
为简化问题,便于模型的建立与求解,针对题目给出的系泊系统(如图1所示)进行以下假设:
1)假设风和水流速度的方向均在同一平面内;
2)由于重物球、锚、锚链体积未知且通常体积较小,忽略其浮力及水流对它们的作用力;
3)假设锚链的每一节都是有质量但没有体积的均匀刚性直杆,每节锚链之间通过节点连接;
4)系泊系统中所有部件的质量都是均匀分布的,质心即为物体的几何中心。

图1 系泊系统示意图
2 系泊系统的设计分析
2.1 系泊系统的受力分析
基于基本假设,对整个系统由上到下进行受力分析[2-3]。其中,浮标是一个底面直径为2 m、高为2 m的圆柱体,受到重力、浮力、风力、第一根钢管(以下简称钢管1,以此类推)的拉力作用。近似认为浮标受力的作用点集中于圆柱体中心轴线的中点上,满足受力平衡。作出浮标的受力示意图(仅表示力的方向,不表示力的大小,下同)如图2所示。

图2 浮标的受力示意图
对于四根直径50 mm、长1 m的圆柱形钢管,它们的受力情况基本是一样的,都受到重力、浮力、上面所连接物体的拉力、下面所连接物体的拉力。其中,重力和浮力的作用点可以认为在钢管中心轴线的中点上;两个拉力的作用点应该分别在钢管上下表面的圆心上。这4个力应该满足受力平衡和力矩平衡。作出单根钢管的受力示意图如图3所示。

图3 单根钢管的受力示意图
钢桶受重力、浮力、钢管4的拉力、锚链的拉力和重物球的拉力。其中,重力和浮力的作用点可以认为在钢桶中心轴线的中点上;3个拉力的作用点分别在钢桶上下表面的圆心上。这5个力应该满足受力平衡和力矩平衡。作出钢桶的受力示意图如图4所示。

图4 钢桶的受力示意图
锚链的受力分析较为复杂。锚链的每一节都可以看作是一节短杆。由于锚链较细,忽略其受到的浮力,将一节链环简化为有质量但没有体积的均匀刚性直杆。每节锚链均受到重力、上下物体对它的拉力。其中重力的作用点在直杆的中点处,上下拉力的作用点分别在两个端点。这3个力应该满足受力平衡和力矩平衡。做出单节锚链的受力示意图如图5所示。

图5 单节链环的受力示意图
根据以上受力分析,我们可以对每个对象列出受力平衡和力矩平衡的方程,结合水深的限制条件,求解这些方程,就可以得到整个系统的姿态。
当增加水流速度的影响后,依然可以利用以上方法进行受力分析,并得到相应的受力平衡方程和力矩平衡方程。
2.2 系泊系统的优化设计
当锚链的型号和长度确定时,系泊系统的设计问题主要是重物球质量的单目标优化问题。根据受力分析,重物球质量变大,浮标的吃水深度增加。为了找到满足条件的最优系泊系统,以重物球的质量最小为优化目标,以物体满足的受力平衡、力矩平衡方程组作为约束条件,同时加上水深和角度的限制条件作为约束条件,共同构造出重物球质量求解的单目标优化模型。求解该模型,可得到满足系泊系统工作条件的最小重物球质量。
当锚链型号、长度和重物球质量均不确定时,系泊系统的设计变成多目标的优化问题。分析倾角和系泊系统各个参数间的关系,找到优化目标,仍然以受力平衡和力矩平衡方程组、水深角度的限制条件作为约束条件,建立多目标优化模型。通过对不同型号的锚链分别求解,得到不同锚链对应的最优系泊系统设计。再将这几个方案进行对比,找到最优的系泊系统设计方案。
3 基于受力分析的系泊系统姿态模型
浅海观测网的系泊系统可以认为是由浮标、4节钢管、钢桶、重物球、锚链和锚组成的。在海风、重力等作用力的影响下,整个系泊系统的各个组成部分之间最终会达到相对静止,此时应当满足受力平衡和力矩平衡两个条件。为了便于模型叙述,先对系泊系统的各个部分进行编号如表1所示。

表1 系泊系统各部分编号
设系泊系统所处的水深为H;系统静止时浮标的吃水深度为d0;编号为i的圆柱体底面半径为ri,高为di;编号为i的物体所受的浮力为Ti;编号为i-1的物体对编号为i的物体的拉力为Fi-1,i,拉力与竖直方向的夹角为θi-1;编号为i的物体的倾斜角度为αi。
3.1 系泊系统的受力平衡
通过对各物体分别进行受力分析,可得到在水平和垂直方向上满足的受力平衡方程,联立得到受力平衡方程组:

3.2 系泊系统的力矩平衡分析
作用在物体上的作用力与力臂的乘积称为力矩。对于稳定的系泊系统,系统中每一个物体都应该满足力矩平衡;否则,物体会产生转动。当一个物体在静态平衡时,静作用力是零,对任一点的合力矩也是零[4]。
由于浮标体积较大,可忽略其转动效应,因此浮标的合力矩为零,不进行分析。对于编号的钢管,当其静态平衡时,对任一点的合力矩为零。为了计算简便,选择钢管与上面物体相连的节点作为支点进行分析。可得到力矩平衡方程组:

同时,由于环境的客观限制,有水深条件如下:

综合上述,由式(1)~式(3)可得到系泊系统的姿态满足的数学模型。求解系泊系统姿态模型,可得到钢管与钢桶的倾角αi(i=1,2,3,4,5),锚链形状及浮标的吃水深度d0。
对于浮标的游动区域,由于不同的风向会导致浮标向不同的方向浮动,由此知浮标的游动区域为一圆形。在风速一定的情况下,浮标到锚的最大水平距离称为游动区域半径,表示为:

式中,di为编号i的器件的长度。
通过Matlab编程求解[5],我们得到了海面风速为12 m/s、24 m/s和36 m/s时的系泊系统姿态。将系泊系统各个参数列表展示如表2所示。
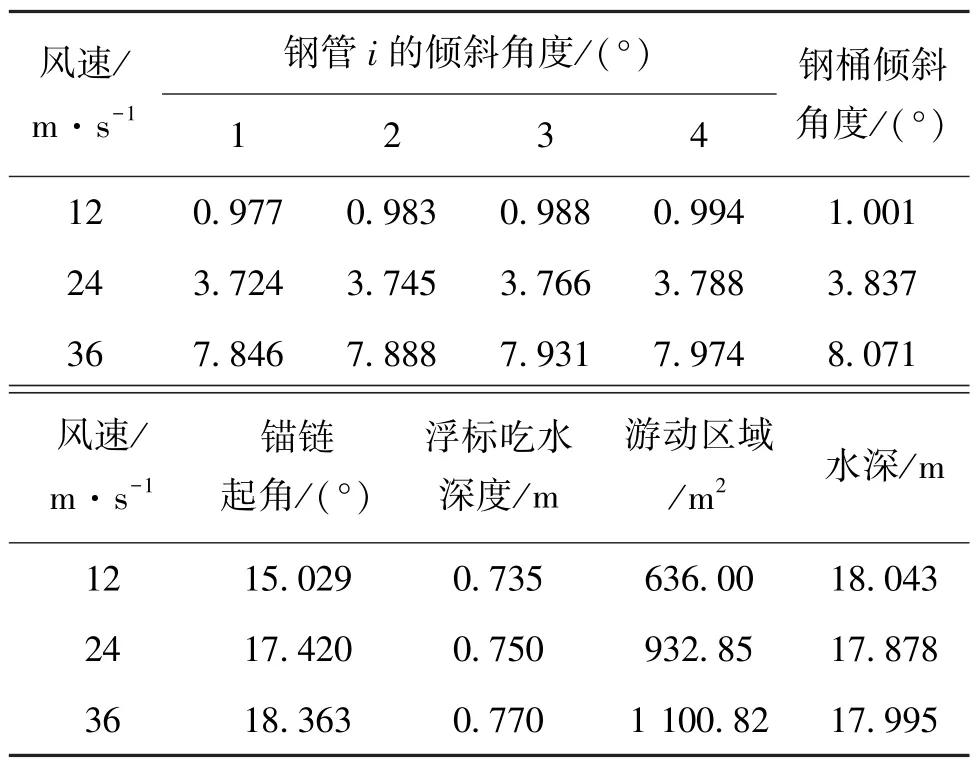
表2 系泊系统姿态参数表
其中,风速为12 m/s时,共有7.35 m的锚链接触地面;风速为24 m/s时,共有3.675 m的锚链接触地面;风速为36 m/s时锚链不存在拖地的情况。
4 系泊系统设计的优化模型
4.1 重物球质量的单目标优化模型
该系泊系统工作时,要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16°,钢桶的倾斜角度(钢桶与竖直线的夹角)不超过5°。当系泊系统在某种环境条件下不能满足工作要求时,需要改变重物球的重量。由于系泊系统要求吃水深度能够尽可能小,则重物球的质量应尽可能小。因此以角度要求及系泊系统姿态模型为约束条件,以重物球质量最小为优化目标,建立单目标优化模型如下[6-7]:

系泊系统的角度约束:

求解上述优化模型,即可得到满足系泊系统设计要求的最小重物球质量。
利用Matlab编程寻找合适的重物球质量[8],得到风速36 m/s时,满足角度要求的条件下最小的重物球质量为1 790 kg。求解得到的新的系泊系统的参数如表3所示。
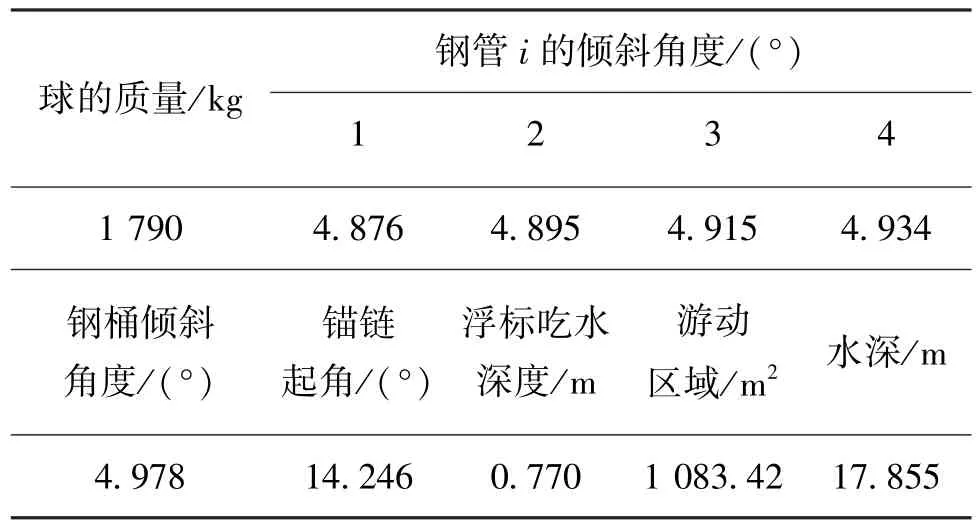
表3 风速36 m/s时的新系泊系统参数表
4.2 系泊系统设计的多目标优化模型
对于同一个系泊系统,水深越深、风速和水速越大、风速和水速的夹角越小,钢桶和锚链的倾角都会随之增大,也就说明环境越恶劣。只要设计的系泊系统能够在最恶劣环境下满足工作要求,那么在其他环境中也一定可以满足设计要求。由此得到使钢桶和锚链点倾角尽可能大的极端恶劣环境条件:水深20 m,海水水流流向与风向一致,海水流速为1.5 m/s,风速为36 m/s。
系泊系统的设计目标是使浮标的吃水深度、游动区域和钢桶的倾斜角度尽可能小,这3项目标可转化为新目标——锚链链长L及重物球质量尽可能小。
5种不同型号的锚链在相同的恶劣环境条件下可得到5种不同的最优系泊系统设计,其中锚链长度和重物球质量最小的设计即为最优设计。
设wk( k=1,2,3,4,5)为第i种锚链每节链环单位长度的质量,vf为水流速度,ri( i=0,1,2,3,4,5)是编号为 i的部件的半径,则第 i( i=1,2,3,4,5)个部件所受到的水流力为:

以锚链长度L和重物球质量mq为目标构建双目标优化模型[9]。

系泊系统的角度约束:
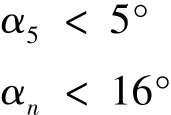
为了找到不同型号锚链对应的系泊系统设计,需求解出每个型号对应的优化系泊系统设计方案后,再进行比较,找出给定环境下系泊系统设计方案的最优解。
通过对每一种型号的锚链分别进行编程求解[10-11],我们得到了5种型号锚链各自的最优系泊系统设计方案如表4所示。可以看到,5种最优方案的水深相对误差都不超过3,认为结果与实际情况偏差不大,可以接受。

表4 不同型号锚链的系泊系统设计方案
为了比较不同型号锚链最优设计方案之间的优劣,计算出每个方案的系泊系统姿态参数,列表如表5所示。

表5 不同系泊系统姿态对比
以上5个系泊系统的吃水深度均为1.65 m,钢桶的倾斜角度均为4.97°,型号Ⅴ的浮标游动区域显然最小,并且锚链起角也最小。因此,选定锚链型号Ⅴ对应的设计方案为最优设计方案。具体设计为:选定锚链型号为Ⅴ型,锚链长度为21.600 m,重物球质量为3 590 kg。
5 结束语
本文建立了系泊系统姿态模型,得到了不同给定条件下系泊系统的姿态。对于不满足工作要求但锚链型号与长度给定的系泊系统,建立了重物球质量的单目标优化模型,找到了合适的重物球质量,从而调整系泊系统使之满足工作要求。在锚链型号、长度、重物球质量均不确定时,建立系泊系统设计的多目标优化模型,设计出在所给定环境下满足工作要求的最优设计方案。
模型的优点在于模型精度高,所建立的系泊系统姿态模型可以很好地对系泊系统的姿态进行描述;模型的应用范围广,所建立的系泊系统设计模型,可以适用于一定条件范围内的海域,应用范围较大。
缺点在于模型求解复杂,考虑利用悬链线模型改进[12]。在海水中受恒力作用的锚链可近似为数学中的悬链线,可利用悬链线近似锚链的姿态,以此减少原模型求解过程中的遍历次数,可增大求解的便利性。
[1]唐友刚,张素侠,张若瑜,等.深海系泊系统动力特性研究进展[J].海洋工程,2008,26(1):120-126.
[2]王磊.单点系泊系统的动力学研究[D].青岛:中国海洋大学,2012.
[3]徐兴平,童英玉.单点系泊系统动力响应分析[J].石油大学学报(自然科学版),1994(5):74-78.
[4]滕保华,廖旭.大学物理学[M].北京:科学出版社,2010.
[5]张德丰.MATLAB数值分析[M].北京:清华大学出版社,2016.
[6]米尔斯切特.数学建模方法与分析[M].刘来福,黄海洋,杨淳,译.北京:机械工业出版社,2014.
[7]姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2011.
[8]陈杰.MATLAB宝典[M].4版.北京:电子工业出版社,2013.
[9]肖晓伟,肖迪,林锦国,等.多目标优化问题的研究概述[J].计算机应用研究,2011,28(3):805-808.
[10]张利彪,周春光,马铭,等.基于粒子群算法求解多目标优化问题[J].计算机研究与发展,2004,41(7):1286-1291.
[11]王健,赵国生.MATLAB数学建模与仿真[M].北京:电子工业出版社,2013.
[12]周洋.深水悬链线锚泊系统多成分锚泊线设计[D].哈尔滨:哈尔滨工程大学,2008.
