基于选择性维修的装备战场抢修决策建模
2018-01-15曹文斌贾希胜胡起伟苏续军
曹文斌, 贾希胜, 胡起伟, 苏续军
(1. 军械工程学院装备指挥与管理系, 河北 石家庄 050003; 2. 军械工程学院火炮工程系, 河北 石家庄 050003)
0 引 言
战场抢修由战场损伤评估(battlefield damage assessment,BDA)和战场损伤修复(battlefield damage repair,BDR)两部分组成,其中,BDA是BDR的前提和基础[1]。战场损伤评估的实质是对损伤装备进行战场抢修技术决策的过程[2],一直受到研究人员的广泛关注[3-7]。装备战场抢修决策是战场损伤评估的重要内容,解决的是修什么(抢修项目)、怎么修(抢修方法)和由谁修(抢修任务分工)的问题,即决策的目标是确定装备战场抢修方案。目前,部队实施装备战场抢修决策主要依赖于专家经验,虽然有些单位开发了战场损伤评估专家系统[8-10],但面对复杂的装备战场损伤情况,如何根据作战任务和战场抢修时限要求,科学选择确定装备修复项目,进而生成装备抢修方案,现有的评估系统还缺乏有效的辅助决策模型支持。
选择性维修是指在维修资源(如维修时间、费用、器材、人员等)约束下,从一系列待修项目中确定所要实施的维修项目的过程。文献[11]于1998年首次提出选择性维修,近年来,逐步受到国内外研究学者的普遍关注,在考虑多种维修方法[12-15]、面向多状态系统[16-17]、考虑系统相关性[18-19]、考虑不同任务特性[20-21]及求解方法[22]等方面,研究建立了多种选择性维修模型。选择性维修与战场抢修有很多相似之处,如:都是面向任务对装备(设备)进行维修(抢修)决策,决策过程都要考虑多资源约束,都不要求恢复装备(设备)的完好状态,而有选择性地确定维修项目等。然而,现有的选择性维修模型主要应用于民用设备领域,多以费用最小为目标或以费用为约束进行维修决策,缺乏时间、人员等资源有限情况下战场抢修决策方面的相关研究。鉴于此,本文将选择性维修理论引入装备战场抢修决策,借鉴选择性维修理论的思路与方法,结合战场抢修的特点,考虑抢修人员、抢修时间、备件等资源有限的复杂情况,以单体装备战场抢修决策为例,研究建立面向随机任务的装备战场抢修决策模型,从而为选择确定装备修复项目、生成装备抢修方案提供辅助决策模型支持。
1 问题描述
战场抢修决策涉及因素众多、问题复杂,为了有针对性地开展建模研究,进行如下假设:
(1) 假设装备发生战损后,抢修人员对受损装备成功实施了损伤检测、定位、分析和判断,判明了装备的损伤部位和程度。按照指挥员的要求,必须在任务间隔tb内恢复装备的基本功能,使其满足下一阶段作战任务使用要求;
(2) 假设装备有多个基本功能部件受损,每个部件有多种抢修方法,包括标准修理方法和应急修复方法,各种抢修方法对装备基本功能的恢复程度不同;
(3) 假设战场情况下用于装备修理所需时间、备件、人员等资源有限,需要对装备抢修措施、抢修任务分工等进行优化;
(4) 假设抢修人员的能力完全一致,且不能多人同时抢修同一部件。
考虑上述情况,假设某装备由n个基本功能部件组成,在执行任务1过程中,由于装备战损,导致任务失败,其任务周期如图1所示。为了恢复其执行作战任务的能力,必须在任务2到达之前的任务间隔期内对其进行抢修。每个部件可采用多种抢修方法,不同的抢修方法的资源消耗及抢修效果均不同。预计任务2会在tb时刻后到达,任务持续时间td为服从某一分布的随机变量。决策者需要根据有限的抢修时间、抢修人员和抢修器材,给出合理的抢修方案,包括抢修部件、抢修方法及抢修任务分工,使得任务2到来之前恢复战损装备的功能状态,且抢修后的装备在任务2的可靠度最大。

图1 任务周期Fig.1 A mission period
2 战场抢修决策建模
2.1 抢修方法建模
2.1.1 抢修方法概述
战场情况下,装备抢修方法很多,一般情况下,在有备件时,会采用备件进行换件抢修;否则,可以采用切换、剪除、拆换、替代、原件修复、制配、重构等7种抢修工作类型[1]对损伤装备进行修复。在抢修方法选择时,抢修人员会优先选择资源消耗少、抢修效果好的抢修方法。但是,通常抢修效果好的方法消耗资源较多,且战场情况下的抢修资源往往有限,因此,对于多部件系统来说,必须通过建立定量化的数学模型,才能科学地分配有限的抢修资源,使抢修后的装备状态最优。建模过程中,最重要的一步是对每个部件的抢修方法、资源消耗及抢修效果三者之间的关系进行建模,现有的不完善维修理论为解决该问题提供了有效途径。描述不完善维修的模型很多[23],这里采用同时考虑工龄和故障率的综合模型,可以描述为
λk(Akr+td)=ak×hk(bk×Ak+td)
(1)
式中,hk(·)表示抢修前部件k的故障率;λk(·)为抢修后部件k的故障率;td表示任务2的执行时间;ak(ak≥1)为故障率调整因子;bk(0≤bk≤1)为工龄减少因子;Ak为抢修前部件k的工龄;Akr为抢修后部件k的虚拟工龄。这种综合模型假设抢修后部件工龄减少,故障率增加,比较适合战场抢修。因为战场抢修多采用应急性的修理方法,虽然可以在短时间内改善部件的功能状态,但是其故障率往往较高。
针对每个部件,抢修人员可以有两种基本的抢修选择:不抢修和抢修。根据抢修效果,可以进一步将抢修分为:换件、最小抢修和介于换件和最小抢修之间的中间状态的抢修,即不完善抢修。如果选择不抢修,则部件的状态保持不变;换件是用新部件替换旧部件;最小抢修属于修复性抢修,是采用最简单的抢修方法,使损伤部件快速恢复到能工作的状态,其工龄和故障率均假设不变;而不完善抢修可以是修复性的也可以是预防性的,能改善部件功能状态,降低部件的有效工龄但同时提高故障率的斜率。不同抢修方法的效果对比如表1所示。

表1 不同抢修方法的效果对比
注:0
2.1.2 基于时间的抢修方法建模
战场情况下,时间是突出的约束资源,因此根据文献[13]中的模型,采用基于时间的不完善维修模型对不同的战场抢修方法建模。标准的修理过程由拆卸部件、修复部件和安装调试部件3个基本步骤组成,则每一种抢修方法所用时间都可以通过这3个步骤所需的时间计算得到。部件k的抢修时间可表示为
(2)
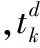
则Yk与lk的值所对应的抢修方法的对应关系如表2所示。

表2 lk的含义
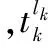
(3)
式中,mk为与部件工龄有关的常数,用于描述部件的“年轻程度”。mk越大,部件越年轻,通常用部件的工龄(Ak)和平均剩余寿命(mean residual life,MRL)表示[7],表达式为
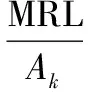
(4)
与工龄减少因子相似,故障率增加因子也取决于投入的可变抢修时间和部件工龄。故障率增加因子模型为
(5)
式中,ζk为常数,决定故障率增加因子的上限值,ζk越大,故障率增加因子的上限值越小。ζk的值可以通过部件历史数据得到[7]。
2.2 抢修人员需求建模
对于这类考虑任务顺序的抢修来说,抢修人员的实际需求量由抢修部件的数量决定。假设现有的抢修人员数量为q,抢修部件的数量为ω。若用Vk表示是否对部件k进行维修,则
抢修部件的数量可表示为
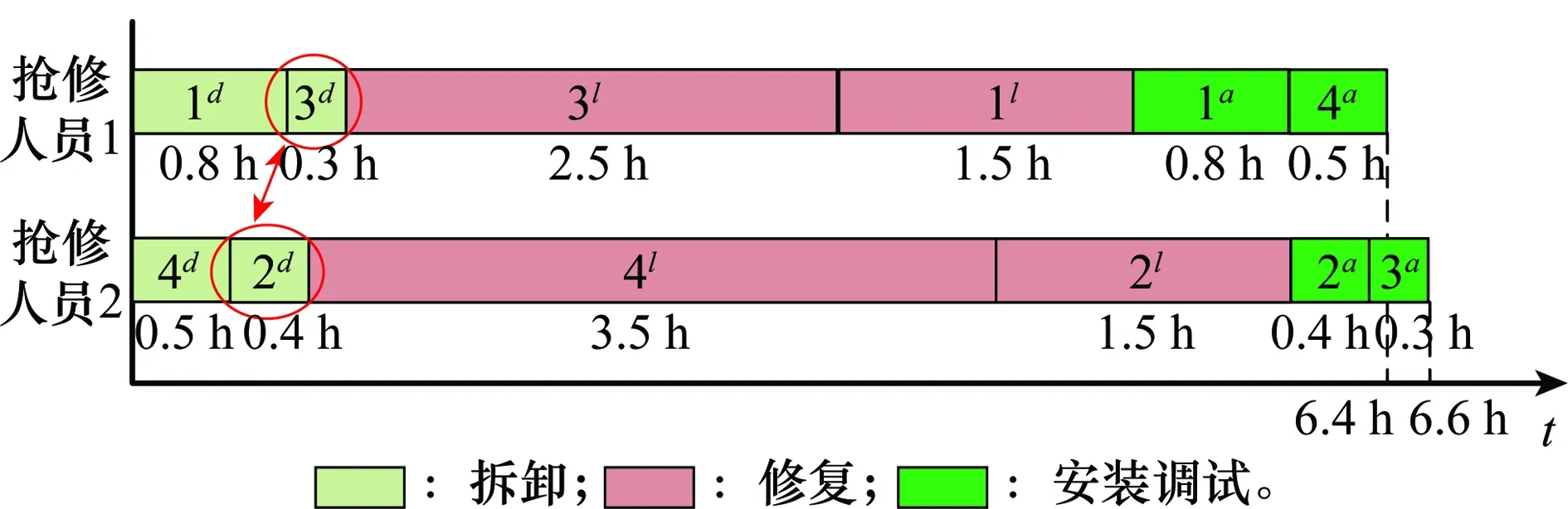
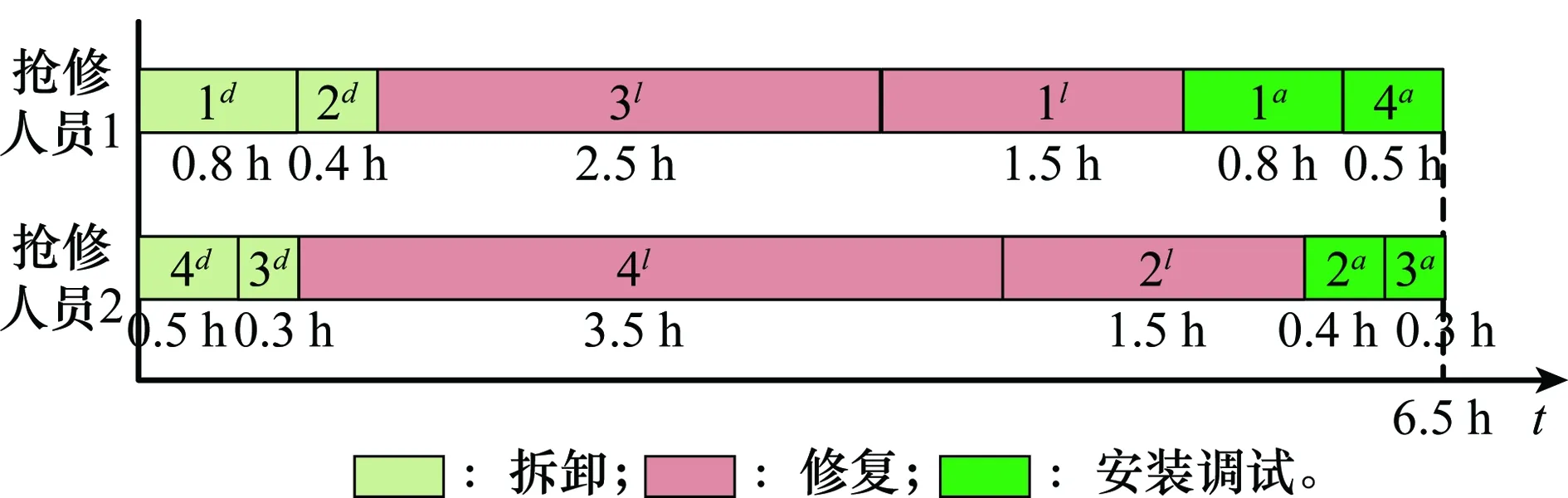
(6)
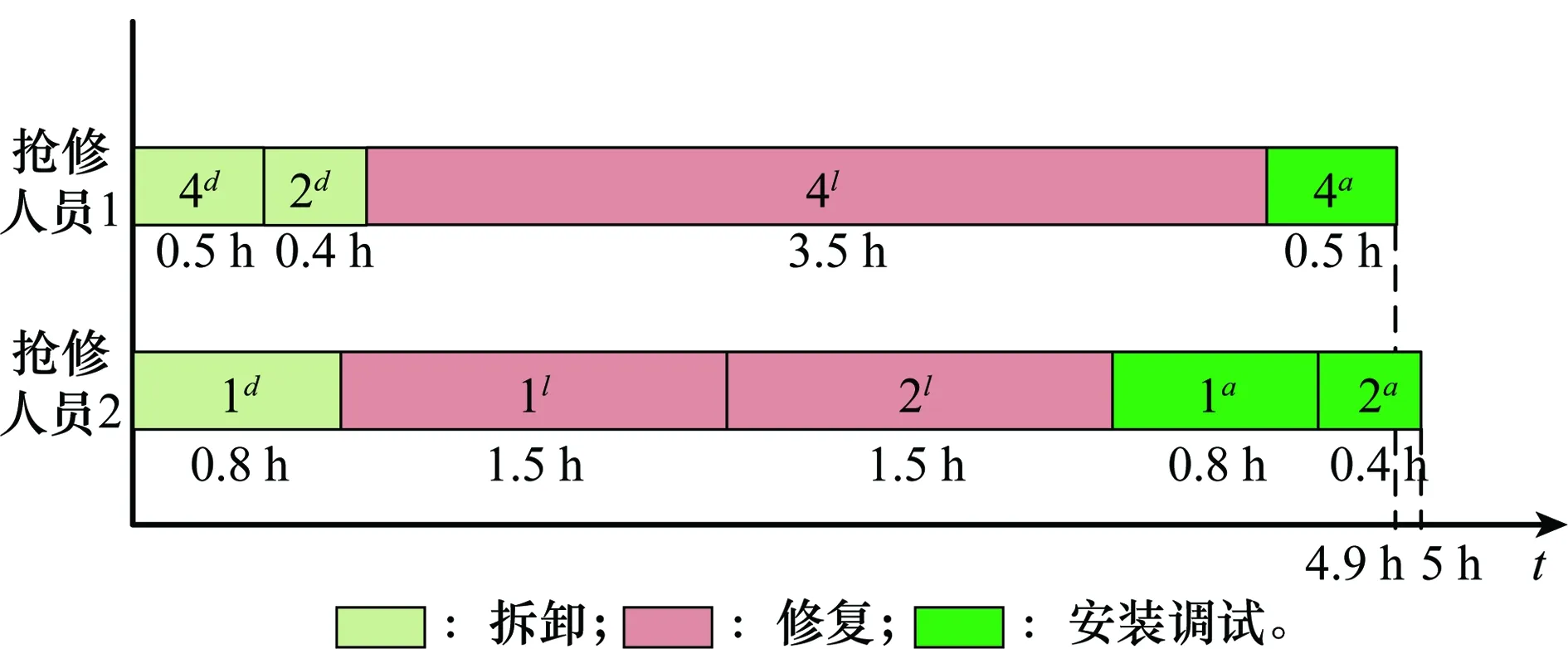
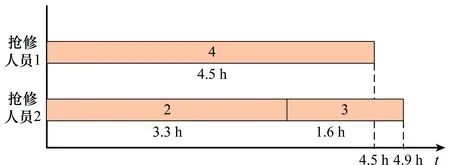
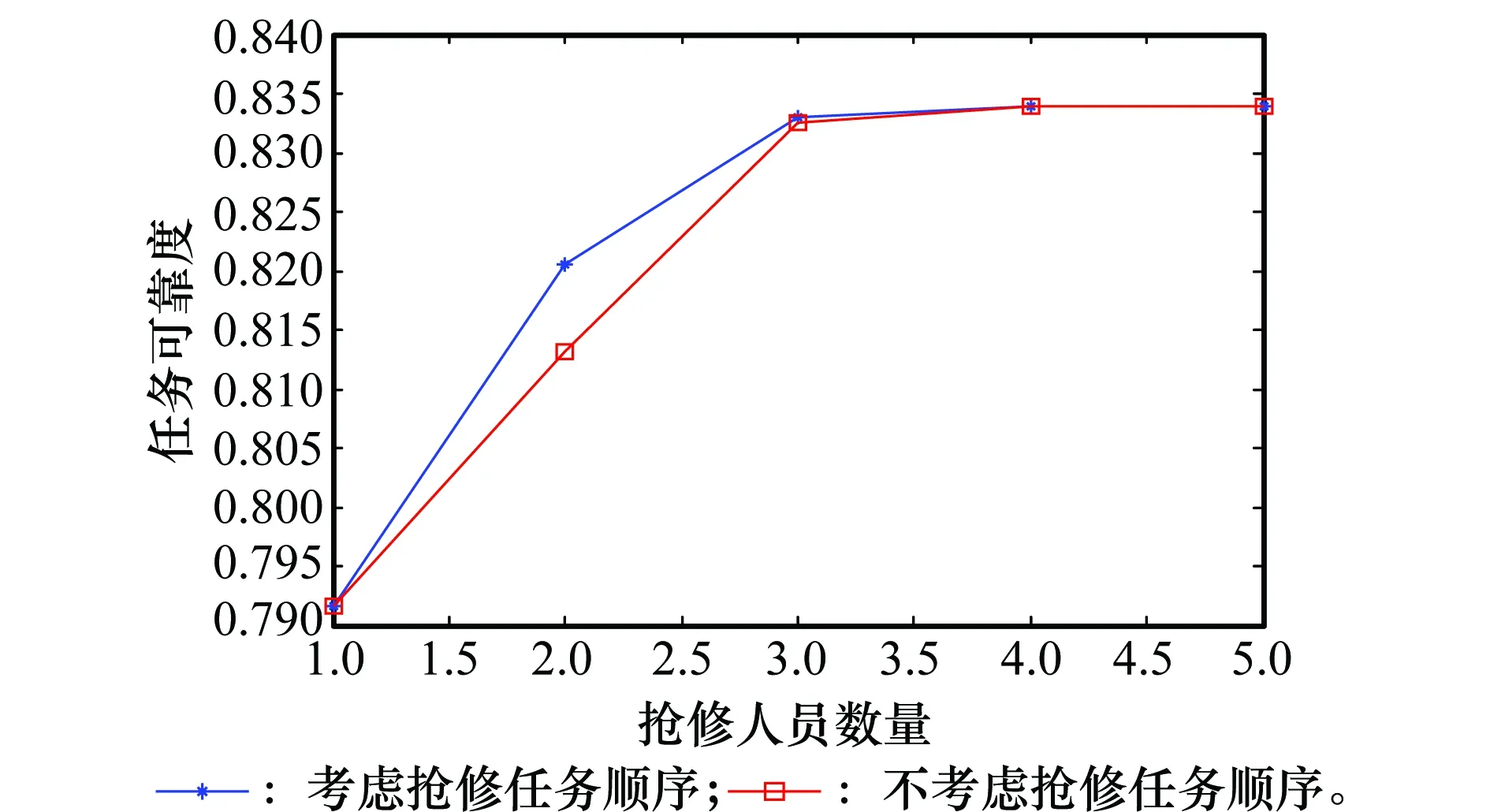
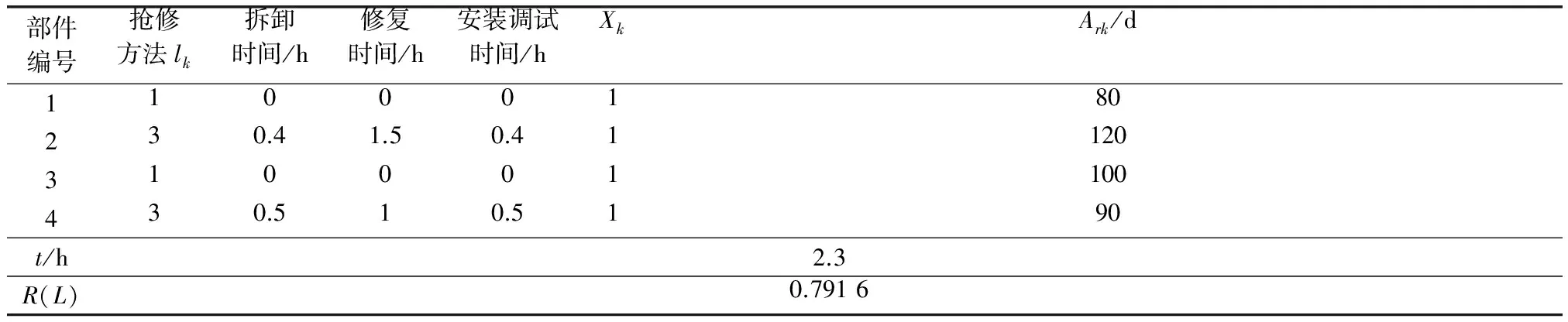
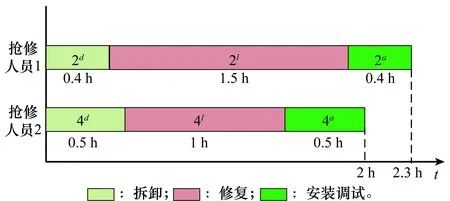
当ω (7) 装备抢修时间由抢修部件数量和抢修人员数量共同决定,这里分3种情况讨论,即q=1,q>1且q=ω和q>1且q≠ω。 (1) 第1种情况:q=1 当只有一个抢修人员(q=1)时,该抢修人员必须承担所有的抢修工作,总抢修时间为所有抢修工作时间之和。对于抢修方案L=(l1,l2,…,lk,…,ln),部件k的抢修时间为 (8) 装备抢修时间为 (9) (2) 第2种情况:q>1且q=ω 当抢修部件数量与抢修人员数量相等时,装备抢修时间为所有部件抢修时间的最大值,即 k=1,2,…,n;q>1且q=ω (10) (3) 第3种情况:当q>1且q≠ω 改进的任务分配算法步骤如下。 步骤2将前q项任务依次分配给q个抢修人员,在任务集合Task中剔除已分配的任务,更新任务集合Task; 步骤3计算每个人员的任务完成时间tc,找到tc最小所对应的抢修人员cmin,将任务集合Task中时间最大的任务分配给cmin。更新任务集合Task,并判断是否为空,若为空,则执行步骤4,否则执行步骤3; 步骤4取任务完成时间最大和最小的抢修人员,分别为cmax和cmin,其完成时间分别为tmax和tmin,分配的任务所对应的时间集合分别为Tmax和Tmin; 步骤5统计抢修人员cmax和cmin所承担的抢修任务数量,分别记为γmax和γmin,抢修任务时间集合分别为Tmax和Tmin。判断是否存在tmax,x∈Tmax(x∈{1,2,…,γmax}),tmin,y∈Tmin(y∈{1,2,…,γmin}),使得 步骤6计算各抢修人员的任务完成时间,并查找任务完成时间最小的抢修人员cmin,计算其任务完成时间tmin,判断该时刻已完成的任务,并将对应的修复任务和安装调试任务加入到任务集合Task中; 步骤7对任务集合Task中的任务按时间由大到小的顺序排列,并将时间最大的任务分配给人员cmin,当同时存在修复任务和安装调试任务时,优先分配抢修任务,同时在任务集合中Task剔除该任务。判断任务集合Task是否为空,若为空,则执行步骤8,否则执行步骤6; 步骤9若将{tmax,x1…tmax,x2}和{tmin,y1…tmin,y2}对应的任务互换,判断任务互换后是否满足任务之间的优先级约束关系(kdfklfka,k=1,2,…,n),若满足则互换,并执行步骤8,否则执行步骤10; q>1且q≠ω,c=1,2,…,q (11) 对于抢修方案L=(l1,l2,…,lk,…,ln),装备抢修时间为 (12) 为了阐述该算法的计算过程,举例进行说明。假设需要抢修4个部件,标号为1~4,每个部件的拆卸时间等于安装调试时间,分别为0.8 h,0.4 h,0.3 h,0.5 h,各部件的抢修时间为1.5 h,1.5 h,2.5 h,3.5 h,抢修人员有2个。根据任务分配算法,初次任务分配的结果如图2所示。此时,tmax=6.6 h,tre=6.4 h,存在tmax-tre=6.6-6.4>0.4-0.3,且满足任务约束关系,因此,可将抢修任务3d和2d互换,调整后的抢修任务分配方案如图3所示。调整后,装备抢修时间为6.5 h,小于调整前的6.6 h。 图2 初次任务分配甘特图Fig.2 Gantt chart of the original maintenance tasks scheduling 图3 调整后的抢修任务分配甘特图Fig.3 Gantt chart of maintenance tasks scheduling after adjustment 假设对装备实施抢修L=(l1,l2,…,lk,…,ln)后,部件k在任务2开始前的状态用Xk表示为 可以得出:Xk=1-(1-Yk)(1-Vk)。根据式(1)、式(3)~式(5),部件的可靠度为 (13) 装备的任务可靠度为 R(L)=φ(rk(lk)),k=1,2,…,n (14) 式中,φ(·)为装备结构函数。当任务持续时间td为服从随机分布f(td)时,装备的任务可靠度为 (15) 假设装备共包含m种部件,第η种部件的数量为nη,则装备部件数量为 (16) 若用Wη κ表示是否更换第η种部件中部件κ,(κ=1,2,…,nη),则 第η种备件的需求量为 (17) 战场抢修决策模型可归纳为 maxR(L,td) (18) s.t.t≤tb (19) q*≤q (20) Bη≤Blη,η=1,2,…,m (21) Xk=1-(1-Yk)(1-Vk),k=1,2,…,n (22) Xk≥Yk,k=1,2,…,n (23) (24) 式中,不等式(19)表示抢修时间不能大于给定的任务间隔时间;不等式(20)表示抢修人员实际需求量不能大于现有的人员数量;不等式(21)表示换件数量不能大于现有的备件数量Blη;不等式(22)、不等式(23)和不等式(24)表示维修前后部件状态约束。 某装备由4个基本功能部件组成,结构如图4所示。 图4 装备结构图Fig.4 Equipment structure 图4中,灰色方框表示战损部件,白色方框表示未故障部件。在执行作战任务过程中由于敌方火力打击导致装备战损,为了能够执行作战任务2,必须对其进行抢修。假设现有2个抢修人员,且当前已经没有备件,即所有的部件都不能进行换件抢修。任务2预计在5 h之后到达,假设任务持续时间服从参数λd=0.25d-1的指数分布。各部件的寿命服从威布尔分布,其分布参数和抢修时间如表3所示。 表3 各部件分布参数和抢修时间 由建立的战场抢修决策模型,得到最优抢修方法组合为L=(3,3,1,4),如表4所示,即对部件1和部件4进行不完善抢修,抢修方法编号分别为3和4,对部件2实施最小抢修,对部件3不进行抢修。装备抢修时间为5 h,可达到的任务可靠度为0.820 5。抢修任务分配甘特图如图5所示,抢修人员1的任务包括:拆卸部件4和部件2,然后对部件4进行修复,最后安装调试部件4,任务完成时间为4.9 h;抢修人员2的任务包括:拆卸部件1,对部件1和部件2进行修复,安装调试部件1和部件2,任务完成时间为5 h。当不考虑抢修任务顺序时,在任务分配时将拆卸、修复和安装调试3个任务视为一个整体。装备的最优抢修方法组合为L=(1,4,3,4),即不对部件1进行修复,对部件2、部件3和部件4实施不完善抢修,抢修方法编号分别为4、3和4,装备抢修时间为4.9 h,抢修后装备任务可靠度为0.813 1。其任务分配甘特图如图6所示,抢修人员1负责抢修部件4,抢修人员2负责抢修部件1和部件2。对比两种抢修方案,可以看出,两种情况下的得到的最优抢修方案不同;与不考虑抢修任务顺序的战场抢修决策结果相比,考虑抢修任务顺序时,战场抢修能够获得较高的任务可靠度。 图5 L=(3,3,1,4)时,考虑抢修任务顺序时任务分配甘特图Fig.5 Gantt chart of maintenance tasks scheduling of scheme L=(3,3,1,4) considering task sequence 部件编号考虑抢修任务顺序抢修方法lk拆卸时间/h修复时间/h安装调试时间/hXkArk/d不考虑抢修任务顺序抢修方法lk拆卸时间/h修复时间/h安装调试时间/hXkArk/d130.81.50.8157.941000180230.41.50.4112040.42.50.4189.6131000110030.310.3166.70440.53.50.5153.6740.53.50.5153.67t/h54.9R(L)0.82050.8131 图6 L=(1,4,3,4)时,不考虑抢修任务顺序时任务分配甘特图Fig.6 Gantt chart of maintenance tasks scheduling of scheme L=(1,4,3,4) without considering task sequence 为了进一步分析抢修决策时考虑抢修任务顺序的优势,分别分析了L=(3,3,1,4)时,不考虑抢修任务顺序的任务分配情况(见图7)和L=(1,4,3,4)时,考虑抢修任务顺序的任务分配情况(见图8),分别与图5、图6进行对比。对比图5和图7可以看出,当L=(3,3,1,4)时,若考虑抢修任务顺序,抢修完成时间为5 h,而不考虑抢修任务顺序,抢修完成时间为5.4 h;对比图6与图8可以发现,当L=(1,4,3,4)时,若考虑抢修任务顺序,其抢修完成时间为4.7 h,而不考虑抢修任务顺序时,抢修完成时间为4.9 h。通过分析结果,可以看出,考虑抢修任务顺序会缩短装备战场抢修时间,这对于有效应对瞬息万变的战场环境具有十分重要的意义。 图7 L=(3,3,1,4)时,不考虑抢修任务顺序时任务分配甘特图Fig.7 Gantt chart of maintenance tasks scheduling of scheme L=(3,3,1,4) without considering task sequence 为了评估抢修人员数量对抢修决策及抢修效果的影响,计算了不同抢修人员数量下,装备最优抢修方案组合及对应的任务可靠度,如图9所示。 图8 L=(1,4,3,4)时,考虑抢修任务顺序时任务分配甘特Fig.8 Gantt chart of maintenance tasks scheduling of scheme L=(1,4,3,4) considering task sequence 图9 抢修人员数量对最优抢修方法组合及任务可靠度的影响Fig.9 Effects of number of maintenance personnel on the optimal maintenance scheme and corresponding mission reliability 从图9中可以得出:①在一定范围内,装备任务可靠度会随着抢修人员数量的增加而增加,最后趋于一个常数;②抢修人员数量不同,最优抢修方案也不同;③不同抢修人员数量下,考虑抢修任务顺序时的任务可靠度不小于不考虑抢修任务顺序时的任务可靠度;④当抢修人员数量为1和抢修人员数量等于抢修部件数量时,考虑抢修任务顺序与不考虑抢修任务顺序时得到的最优抢修方案与任务可靠度都相同。因此,在实际装备抢修过程中,如果能合理规划抢修人员数量,并优化抢修任务分配,则可以充分利用有限的抢修资源,提高抢修效果。 为了分析不完善抢修对装备任务可靠度的影响,仍采用第3.1节的算例进行分析。假设在对部件进行抢修时,不考虑不完善抢修方法,即对所有未故障部件来说,只有不抢修和换件抢修2种选择;而对损伤部件来说,有3种抢修方法选择:不抢修,最小抢修和换件抢修。其他假设条件均不变。此时,由于缺少备件,可供选择的抢修方法组合共有2种:(1,1,1,3)和(1,3,1,3),其中(1,3,1,3)为最优抢修方法组合,如表5所示。即对部件1和部件3不抢修,对部件2和部件4进行最小抢修,总抢修时间为2.3 h,任务可靠度为0.791 6,任务分配甘特图如图10所示。对比表4和表5,可以看出考虑多种抢修方法能够显著提高装备任务可靠度。因此,研究装备战场抢修新技术,不断探索装备战场损伤抢修方法,对于提高装备战时性能具有十分重要的意义。 表5 装备最优抢修方法组合 图10 L=(1,3,1,3)任务分配甘特图Fig.10 Gantt chart of maintenance tasks scheduling ofscheme L=(1,3,1,3) 本文将选择性维修理论引入战场抢修决策,研究了考虑顺序的抢修任务分配算法,建立了备件、抢修时间、抢修人员有限时,面向随机任务的战场抢修决策模型,得到了装备战场抢修方案。研究结果表明:选择性维修可有效解决多资源约束条件下,面向任务的装备战场抢修决策问题;考虑抢修任务顺序时,通过优化抢修任务分工,能够缩短装备战场抢修时间,有效提高资源利用率和装备任务可靠度;当装备有多种抢修方法供选择时,能够显著提高抢修效果。本文研究了单体装备的战场抢修决策问题,针对装备群的战场抢修决策问题,将更为复杂,还需要进一步深入探讨,这也是正在研究的内容。 [1] 李建平, 石全, 甘茂治. 装备战场抢修理论与应用[M]. 北京: 兵器工业出版社, 2000. LI J P, SHI Q, GAN M Z. Battlefield damage repair theory and application[M]. Beijing: Weapons Industry Press, 2000. [2] 王广彦, 胡起伟, 王润生. 基于贝叶斯网络的装备战场损伤评估模型[J]. 兵工学报, 2007, 28(11): 1351-1356. WANG G Y, HU Q W, WANG R S. The assessment model of armament battlefield damage based on Bayesian network[J]. Acta Armamentarii, 2007, 28(11): 1351-1356. [3] 王广彦,胡起伟,刘伟.装备战斗损伤组合建模与仿真技术研究[J]. 兵工学报,2012,33(10): 1266-1275. WANG G Y, HU Q W, LIU W. Study on composable modeling and simulating technology for equipment battlefield damage[J]. Acta Armamentarii, 2012, 33(10): 1266-1275. [4] 王润生,贾希胜,王广彦,等.基于案例的战场损伤评估研究[J].兵工学报,2006,27(6): 1086-1089. WANG R S, JIA X S, WANG G Y, et al. A study of battlefield damage assessment with case-based reasoning[J]. Acta Armamentarii, 2006, 27(6): 1086-1089. [5] 曹继平,宋建设,古西睿,等.战场抢修多需求点多资源二层优化调度模型[J].系统工程与电子技术,2008,30(8):1510-1613. CAO J P, SONG J S, GU X R, et al. Optimization dispatching model on multi-requirement points and multi-resources of battlefield maintenance[J]. Systems Engineering and Electronics, 2008, 30(8): 1510-1613. [6] 郭军, 宋建设, 曹继平, 等. 战场抢修资源重组决策方法[J]. 系统工程与电子技术, 2014, 36(2): 306-311. GUO J, SONG J S, CAO J P, et al. Battlefield urgent maintenance resource recombination decision making[J]. Systems Engineering and Electronics, 2014, 36(2): 306-311. [7] 王润生,贾希胜,王卫国,等.基于贝叶斯网络的损伤定位研究[J].兵工学报,2006,27(4):726-730. WANG R S, JIA X S, WANG W G, et al. The damage reason location based on Bayesian networks[J]. Acta Armamentarii, 2006, 27(4): 726-730. [8] 胡起伟,石全,王广彦,等.面向战损模拟的战损等级评定原理及系统实现[J].计算机仿真,2005,22(8):12-15. HU Q W, SHI Q, WANG G Y, et al. Fundamentals and system implementation of the battle damage level assessment applied to battle damage simulation system[J]. Computer Simulation, 2005, 22(8): 12-15. [9] 王润生, 贾希胜, 王润泉. 基于案例的战场损伤评估智能化框架研究[J]. 计算机工程, 2006, 32(7): 174-176. WANG R S, JIA X S, WANG R Q. Study of intelligence frame based on case of battlefield damage assessment[J]. Computer Engineering, 2006, 32(7): 174-176. [10] 黄惠南. 雷达装备战场损伤评估与修复专家系统研究[D]. 长沙: 国防科学技术大学, 2005. HUANG H N. Study on expert system of radar’s battlefield damage assessment and repair[D]. Changsha: National University of Defense Technology, 2005. [11] RICE W F, CASSADY C R, NACHLAS J A. Optimal maintenance plans under limited maintenance time[C]∥Proc.of the Industrial Engineering Research Conference, 1998. [12] CASSADY C R, JR W P M, POHL E A. Selective maintenance for support equipment involving multiple maintenance actions[J]. European Journal of Operational Research, 2001, 129(2): 252-258. [13] PANDY M, ZUO M J, RAMIN M R, et al. Selective maintenance for binary systems under imperfect repair[J]. Reliability Engineering and System Safety, 2013, 113(1): 42-51. [14] KHATAB A, AGHEZZAF E H. Selective maintenance optimization when quality of imperfect maintenance actions are stochastic[J]. Reliability Engineering and System Safety, 2016, 150: 182-189. [15] 朱海平,郭磊,刘繁茂,等.生产批量约束下的串并联系统选择性维修方法[J].计算机集成制造系统,2011,17(2):419-424. ZHU H P, GUO L, LIU F M, et al. Selective maintenance model for series-parallel system under production lot constraint[J]. Computer Integrated Manufacturing Systems, 2011, 17(2): 419-424. [16] LIU Y, HUANG H Z. Optimal selective maintenance for multi-state systems under imperfect maintenance[J]. IEEE Trans.on Reliability, 2010, 59(2): 356-367. [17] PANDEY M, ZUO M J, MOGHADDASS R. Selective maintenance modeling for a multistate system with multistate components under imperfect maintenance[J]. IIE Transactions, 2013, 45(11): 1221-1234. [18] DAO C D, ZUO M J, PANDEY M. Selective maintenance for multi-state series-parallel systems under economic dependence[J]. Reliability Engineering and System Safety,2014,121(1):240-249. [19] MAAROUFI G, CHELBI A, REZG N. Optimal selective renewal policy for systems subject to propagated failures with global effect and failure isolation phenomena[J]. Reliability Engineering and System Safety, 2013, 114(6): 61-70. [20] MAILLART L M, CASSADY C R, RAINWATER C, et al. Selective maintenance decision-making over extended planning horizons[J].IEEE Trans.on Reliability,2009,58(3):462-469. [21] SCHNEIDER K, CASSADY C R. Evaluation and comparison of alternative fleet-level selective maintenance models[J]. Reliability Engineering and System Safety, 2015, 134: 178-187. [22] 徐庆征, 郭乐勐. 串并联系统选择性维修问题的方法研究[J]. 机械设计与制造, 2016(1): 61-65. XU Q Z, GUO L M. Method for solving the selective maintenance problem for series-parallel system[J]. Machinery Design & Manufacture, 2016(1): 61-65. [23] PHAM H, WANG H Z. Imperfect maintenance[J]. European Journal of Operational Research, 1996, 94(3): 425-438. [24] 王正元,朱昱,宋建社,等.动态维修任务调度的优化方法[J].机械工程学报,2008, 44(1): 92-97. WANG Z Y, ZHU Y, SONG J S, et al. Optimal method on dynamic maintenance task scheduling[J]. Chinese Journal of Mechanical Engineering, 2008, 44(1): 92-97.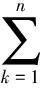
2.3 抢修时间需求建模
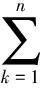

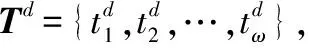
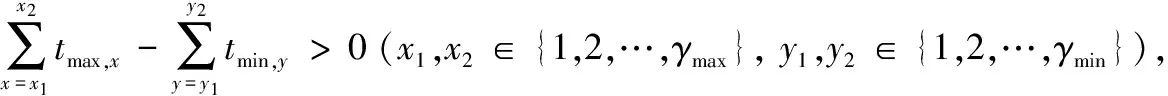
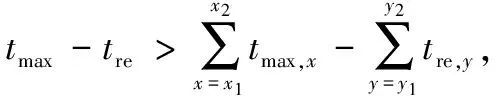

2.4 抢修决策建模

3 算例分析



3.1 抢修任务顺序对抢修任务分配的影响

3.2 抢修人员数量对任务可靠度的影响

3.3 不完善抢修方法对任务可靠度的影响
4 结 论
