小波分析在GPS卫星故障检测中的应用
2018-01-15,,*
,,*
1. 西北工业大学 航天学院,西安 710072 2. 陕西省空天飞行设计重点实验室,西安 710072
全球定位系统(Global Positioning System,GPS)自主完整性检测(Receiver Autonomous Integrity Monitoring,RAIM)技术已成为航空航天导航系统中的研究热点,其目的是在导航过程中检测出发生故障的卫星,并保障导航定位精度。实现RAIM主要有基于快照(Snapshot)和基于时间冗余两种方法。 Snapshot法利用冗余观测量进行集合一致性检验,从而实现对故障的检测和隔离,主要有奇偶空间法(Parity)和最小二乘残差法(SSE)[1]。这两种方法都要求可见星数量大于4颗才能进行卫星故障检测,已有文献证明这两种方法在故障检测方面等价[2]。基于卡尔曼滤波的故障检测法已得到广泛研究[3],该方法利用时间冗余去除对瞬时可见星数目要求较多的限制,却存在依赖准确系统模型、对微小故障漏检误检、检验延迟等问题。
小波分析(Wavelet Analysis)是近20年来发展起来的数学分支。在航空航天领域里,对航空发动机、卫星姿控、组合导航等系统的信息处理与分析中也都少量应用到了小波分析。值得注意的是小波分析非常适合于分析非平稳信号,是故障诊断中处理信号较为理想的工具,通过小波分析可以构造故障诊断所需的特征或直接提取对诊断有用的信息[4]。
本文重点针对基于卡尔曼滤波的故障检测法所存在的问题,将小波分析理论应用到GPS卫星故障检测中,对GPS接收机的伪距观测信息和位置定位信息进行数据处理,通过在不同尺度下的奇异性变化找到信号突变点来进行故障检测。与基于卡尔曼滤波的故障检测法相比,本文提出的故障检测法不仅可以实现接收机自主快速、及时、准确检测出多种模式的卫星故障,没有可见星数量限制,而且该检测方法简洁直观,具有较强的实用性。
1 基于卡尔曼滤波的卫星故障检 测法
1.1 GPS系统模型
tk观测历元时,GPS系统状态方程为:
式中:Xk=[x,y,z,Δt]是k时刻的状态矢量,包括接收机位置矢量和时钟误差;Φk,k-1为状态方程的一步状态转移矩阵;Wk-1为系统噪声矢量。
伪距观测方程为:
式中:ρi为观测伪距,下标i表示第i颗卫星;Ri=[(x-xsi)2+(y-ysi)2+(z-zsi)2]1/2为用户到卫星的位置;x,y,z和xsi,ysi,zsi分别为用户和第i颗卫星在地球坐标系中的位置;lu为用户时钟误差对应的距离。将式(2)线性化可得测量方程为:
式中:Zk为m维观测矢量即伪距观测量;Vk为观测噪声矢量。Vk和Wk-1为互不相关的高斯白噪声序列。
1.2 残差χ2故障检测方法
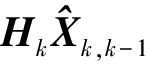
系统无故障时,残差rk是零均值高斯白噪声;反之存在故障时,残差rk均值发生偏移不再为零。对残差rk作二元假设,即:
式中:μ为残差rk的均值;Ak为残差rk的方差。检测统计量构造为:
根据统计分布理论,当无故障时,λm服从自由度为m的χ2分布,m为观测量维数。设允许的虚预警率α,根据奈曼-皮尔逊准则,可由χ2分布求出阈值TD。当λm “小波”指的均值为零且在频域内能量局部化的函数,其波形表现为两端衰减为零的小波形。小波分析的基本思想是用一族小波函数系表示(逼近)函数,小波函数系是通过基本小波Ψ(t)进过平移和伸缩得到的,用其变换系数即可描述原来的函数[4]。基本小波Ψ(t)∈L1(R)∩L2(R) 的小波变换定义为: 式中:a为尺度变换参数,决定小波变换的频率信息;b为平移变换参数,决定小波变换的时域信息。可以看出小波分析兼具时频域的特征。对于信号f(t)∈L2(R),其连续小波变换是将Ψ(t)做平移后,在不同尺度(频率)下和信号f(t)作内积: 相应的重构公式为: GPS卫星发生故障时往往会表现为接收机可测数据即伪距观测数据和位置定位数据出现局部突变,因此可以将这两个数据作为被处理信号,利用小波变换理论处理量测序列,识别异常点进而判断是否发生故障。只需对一个方向的定位数据进行一次小波分析便可实现对故障的检测;故障隔离则需要对多颗卫星的伪距观测数据进行处理。 按照Mallat算法所述,待处理信号被分解之后,实质上是被分解为一个低频分量CM和多尺度下的高频分量D,这些高频分量中就包含有信号局部突变的信息特征即代表故障的发生,表达公式如下: 通过小波多尺度分解所得的高频信号,实质上可以看成一个矩阵,其模值为: 这里定义:设对任意x∈[x0-h,x0+h]有 |Wf(s,x)|≤|Wf(s,x0)|,s=1,2,…,M, 则称x0为小波变换在尺度s下的局部极值点。 GPS卫星故障发生时,表现为被处理信号的小波变换的模在奇异点出现局部极值。通过正常无故障情况下的局部极值变化范围可以确定一个阈值TD,则故障判定准则为: 式中:k=1,2,…,M;j=0,1,2,…,N-1。 根据理论分析,可以在高频分量中确定出现故障时间段,并利用小波信号奇异性确定准确的时间点[7]。对于多尺度小波分析,当分解尺度增加时,由于噪声而引起的小波变换的模极值点迅速减小,信号自身奇异点的变换模的极大值点得以显露,因此能够更加明显地检测出故障的发生。 为了更加真实仿真GPS导航定位全过程,本文建立了GPS卫星星座的全部24颗卫星模型,各颗卫星轨道参数已有文献给出[8]。无论是基于EKF的故障检测方法还是基于小波分析的故障检测方法都没有可见星数目的限制,故本文为保证定位精度采用最佳几何精度衰减因子(GDOP)方法在多颗可见星中找到4颗最佳星座进行导航解算,并在其中一颗星上设置故障。 设仿真时长为1 000 s,单位步长为1 s,用户接收机安装于一个向东作匀速直线运动的飞行器上,起始经度为34.24°,纬度为108.9°,高度为10 000 m,飞行速度为300 m/s。在不同观测点上设置3种故障模式:1)慢变模式,故障发生时间为100 s,大小为200×(t-100)m;2)阶跃模式,故障发生时间为40 s,大小为200 m;3)突变模式,故障发生时间为700 s,大小为200 m。图2给出了故障设置前后x位置定位误差的对比。从图中可以看出,在未加入故障的情况下,x位置定位误差稳定在20 m范围内,没有波动;加入3种故障模式之后,从故障设置开始点起,定位误差开始增大,由此可见GPS卫星发生故障时会导致接收机位置定位数据出现局部突变。 首先,基于EKF的GPS卫星故障检测进行了仿真。设虚预警率α=0.01,根据奈曼-皮尔逊准则得故障检测阈值TD=14.9。设观测噪声均值为0,标准差为30 m。图3为引入故障后的伪距残差卡方检测量示意。从图中可以发现当卫星发生故障时,伪距残差卡方检测量有大幅度的增加,可以检测出故障的发生;但是,当慢变故障发生时(100 s),出现了严重的检测延迟现象,这是因为慢变故障对于系统的影响需要随着故障量的累积才能显现出来;故障结束时报警会持续一段时间,这是由于较大的故障使得滤波器估计值偏离真实值较大,需要一定的时间去恢复精度。 然后,利用Daubechies小波系选取不同的分解层数将待检测的采样信号f(n)分解为高频分量和低频分量,图4为以故障卫星伪距测量数据为被处理信号的仿真结果,图5为3种故障模式发生时伪距测量信号高频d1层的局部放大,图6为以x位置定位信息为被处理信号的仿真结果。从图4中伪距测量信号的小波分解细节和图6中x位置定位信息的小波分解细节都可以清楚地看出:1)低频分量包含了信号的基本趋势,而高频分量则在细节上显示出信号的具体信息特征,更为有效地显示了信号的突变情况。2)高频分量第一层d1及第二层d2数据在100 s,400 s,700 s时发生了明显的突变,因此可以及时准确地判定故障发生。3)检测延迟现象得到有效改善。4)当阶跃故障(400 s)和突变故障(700 s)发生时,高频信号迅速突变;当慢变故障发生时(100 s)高频信号也在缓慢增加,可见通过基于小波分析的故障检测法可以及时、准确、直观地检测出突变及慢变故障信息。 最后,为了研究不同基本小波对卫星故障检测的效果,以重构误差为衡量标准,通过仿真可以得到以两种基础小波(Daubechies小波和Symlets小波)对伪距观测数据进行小波分解重构之后得到的重构误差。使用Symlets小波为基本小波进行小波分解与重构,得到其分解重构误差大小为2.855×10-8,该误差远远大于使用Daubechies小波为基本小波得到的重构误差1.874 5×10-11。因此,单从重构误差角度来说,采用以Daubechies小波为基本小波的小波分解更适合于GPS卫星故障检测。 针对基于卡尔曼滤波的故障检测法所存在的问题,本文提出一种基于小波分析的GPS卫星故障检测法,通过仿真结果可以得出以下结论: 1)使用该方法可以实现接收机自主地进行多种GPS卫星故障检测,对可见星数量没有限制。检测效果明显,检测方法简洁直观,易于工程实现; 2)与基于EKF的GPS卫星故障检测方法相比,该方法不依赖数学模型,且具有更高的检验灵敏度,检验延迟现象得到有效改善,能够及时发现信号突变以检测出故障的发生; 3)该方法不仅对突变的硬故障有非常好的检测效果,对慢变的软故障也具有较好的检测效果; 4)验证了小波分析在GPS卫星故障检测中应用的可行性,说明完全可将小波分析应用到导航系统的自主完整性检测中。为了进一步提升导航系统的安全稳定性,今后需要继续研究如何更为科学合理地选取基本小波和如何划定分解层这两个问题。 References) [1] BROWN R GROVER. A baseline GPS RAIM scheme and a note on the equivalence of three RAIM method[J]. Journal of the Institute of Navigation,1992,38(3):301-314. [2] 刘准,陈哲. GPS自主式完整性检测技术研究[J]. 北京航空航天大学学报,2003,(8):673-676. LIN Z, CHEN Z. Study on GPS receiver autonomous integrity monitoring[J].Journal of Beijing University of Aeronautics and Astronautics, 2003, (8):673-676 (in Chinese). [3] 刘剑慰,姜斌.基于卡尔曼滤波的GPS导航系统故障检测[J].东南大学学报(自然科学版),2008, 38(S2):46-49. LIU J W, JIANG B. Fault detection in GPS navigation system based on Kalman filter[J]. Journal of Southeast University (Natural Science Edition), 2008, 38(S2):46-49 (in Chinese). [4] 刘明才.小波分析及其应用[M].2版.北京:清华大学出版社,2013:22-34. LIU M C. Wavelet analysis and application[M]. 2nd ed. Beijing: Tsinghua University Press, 2013:22-34(in Chinese). [5] 周富相,郑晓晶. 基于卡尔曼滤波的RAIM方案研究[J]. 无线电工程,2010,(11):36-39. ZHOU F X, ZHENG X J.Research on receiver automatic integrity monitoring scheme based on Kalman filtering[J]. Radio Engineering, 2010 (11):36-39(in Chinese). [6] 杨永明. GPS接收机定位可靠性数据处理算法研究[D].沈阳:沈阳航空航天大学,2015. YANG Y M.Research on data processing algorithm in GPS receiver positioning reliability[D].Shenyang:Shenyang Aerospace University, 2015(in Chinese). [7] 夏奇,郝顺义,常诚,等. 基于小波分析的RAIM算法卫星故障检测研究[J]. 计算机测量与控制,2014(5):1320-1322. XIA Q, HAO S Y, CHANG C, et al. A research on failure detection of wavelet transformation based RAIM algorithm [J]. Computer Measurement and Control, 2014 (5):1320-1322(in Chinese). [8] 袁建平,罗建军,岳晓奎,等.卫星导航原理与应用[M].北京:中国宇航出版社,2003:47-139. YUAN J P, LUO J J, YUE X K, et al.Satellite navigation system: principle and application [M]. Beijing:China Aerospace Publishing House, 2003:47-139(in Chinese). [9] 飞思科技产品研发中心.小波分析理论与MATLAB7实现[M].北京:电子工业出版社,2005:441-442. Product Development Center of FECIT. Wavelet analysis theory and Matlab7 application [M]. Beijing: Publishing Housing of Electronics Industry, 2005:441-442(in Chinese). [10] AKANSU A N, TAZEBAY M V, MEDLEY M J, et al. Wavelet and subband transforms: fundamentals and communication applications[J]. IEEE Communications Magazine, 1997, 35(12):104-115. [11] HAFEZ A G, GHAMRY E, YAYAMA H, et al. A wavelet spectral analysis technique for automatic detection of geomagnetic sudden commencements [J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(11):4503-4512. [12] 李根成,王镛根. 卡尔曼滤波在故障诊断中的应用[J]. 航空兵器,1995,(5):23-25. LI G C, WANG Y G.Application of Kalman filter in fault diagnosis [J]. Aero Weaponry, 1995, (5):23-25 (in Chinese). [13] 章岳鹏. 基于小波分析的故障检测与诊断系统的研究[D].成都:电子科技大学,2012. ZHANG Y P. Research on fault detection and diagnosis system based on wavelet analysis[D]. Chengdu:University of Electronic Science and Technology of China, 2012(in Chinese). [14] 王胜. 故障诊断的基本理论和方法综述[J]. 广州大学学报(综合版),1989(1):50-55. WANG S.Summary of basic theory and methods of fault diagnosis[J]. Journal of Guangzhou University (Integrated Edition), 1989 (1):50-55(in Chinese). [15] 任烨. 多场景下的GNSS完好性监测方法研究[D].西安:中国科学院研究生院(国家授时中心),2016. REN Y.The research on GNSS integrity monitoring under multi-Scenarios[D]. Xi′an:Graduate University of Chinese Academy of Sciences (National Time Service Center, Chinese Academy of Sciences), 2016(in Chinese).2 基于小波分析的卫星故障检测法
2.1 小波分析基本理论
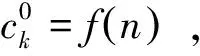
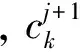
2.2 故障判定准则
3 仿真分析
4 结束语
