无源互调对直扩系统伪码捕获性能的影响

，，

1. 北京理工大学 信息与电子学院，北京 100081 2. 中国电子科技集团公司 电子科学研究院，北京 100041

无源互调(Passive InterModulation，PIM)是指系统多个不同频率的载波信号通过系统无源器件的混频效应而相互调制所引起对系统的额外干扰[1-2]。无线通信系统中的无源互调是由发射系统中各种无源器件(如双工器、天线、馈线、射频线连接头等)的非线性特性引起的[3]。如果这些互调失真信号落入接收频带内，且功率超过接收机基底噪声，会使接收信号的信噪比下降，使接收机的误码率降低甚至无法正常工作，严重影响通信系统的容量和质量[4-6]。目前已经证实，无源互调对卫星通信系统能够产生不同程度的影响。确定无源互调干扰强度与通信系统、导航系统性能恶化之间的定量关系，则可在工程实践中合理制定系统无源互调最大容限，减小总体方案设计的不确定性。

目前国内外对PIM干扰信号参数与通信接收机关键指标之间的关系已有一定研究成果，具有代表性的工作包括文献[7]建立了用于研究高阶互调产物的模型，将干扰建模为最大功率互调项、其他互调项和接收机噪声的叠加，并推导了该模型的分布特性。文献[7]的研究表明，高阶互调产物对系统的影响不可忽视。文献[8]分析了无源互调对通信系统抗噪声性能的影响并计算了PIM干扰下的正交相移键控(Quadrature Phase Shift Keyin,QPSK)误码率。文献[9]研究了PIM对于高斯白噪声环境下的MPSK调制方式信号在误码率和误符号率方面的影响。现有的研究成果集中于分析双载波PIM对通信系统误码率的影响；而且，在已有分析中，对PIM干扰信号的假设过于理想，无法实现PIM对通信系统性能影响的精准预测；此外，从国内外公开论文尚未发现研究无源互调对通信接收机捕获性能的影响分析。

由于扩频通信系统的抗干扰和可测距等优点，已被广泛应用于卫星深空通信、卫星导航与测控系统中，而其中伪码捕获环节是信号同步与正常传输的关键，成功捕获信号才能帮助接收机初始化跟踪环路并开始跟踪信号[10]。本文在已有研究[2]的基础上，分析PIM对卫星接收机伪码捕获性能的影响，结合概率密度分析方法，研究PIM对平方律检波器捕获方法和平方检波累积器捕获方法性能的影响，仿真得到捕获检测概率与伪码长度、信干噪比和PIM阶次的关系，以帮助制定卫星研制的PIM指标。

1 PIM信号的统计特性分析

无源互调是由微波无源部件的非线性特性引起的，主要分为接触非线性和材料非线性，材料非线性是由铁磁、碳纤维等合金材料的固有非线性特性引起的，接触非线性是由实际部件中两个导体接触的不理想产生的[11-12]。无源互调信号频率是激励信号基波频率的线性组合，n个载波经过非线性效应后输出频率为:

式中：mi(i=1,2,…,n) 为整数；fi(i=1,2,…,n)为各载波频率。互调阶次：

通常将满足m1+m2+…+mn=1这一条件的互调产物称为I区互调产物，I区互调产物的阶次为奇数，频率在直流和2次谐波之间，接近激励信号的频率[13]。在无线通信中，通常上下行信号处于同一波段，上下行频段划分也较近，因此本文重点研究对接收机造成较大干扰的I区PIM产物。

对于卫星载荷，以双载波BPSK调制信号作为下行大功率激励信号为例，2路调制信号X(t)可表示为：

式中：Bi、θi分别为频率为fi的独立载波的包络和相位。

对于非线性现象，通常采用幂级数模型来描述[7]：

式中：Y(t)为输出的PIM信号；ai(i=1,2,…,n)为级数的系数，可以为实数或复数。

若仅考虑I区互调产物，则落入接收频带的N阶(N=2p+1)互调产物可以写作：

激励信号采用随机数据，可得如图1所示的9阶PIM概率分布，可见PIM信号的概率分布呈倒喇叭形状，介于高斯分布和柯西分布之间，可采用修正的柯西分布来描述。

N阶PIM的概率分布可以用修正柯西分布来近似，表示为[14]：

其中，

式中：λ为尺度参数，控制概率分布的集中程度；K为高斯修正参数。

2 PIM干扰下直扩系统模型

无源互调干扰下的典型直扩通信系统框图如图2所示，扩频接收机需要对下变频后的接收信号进行相关解扩剥离伪码，然后才能进行解调，恢复出传输信息。

伪码捕获是对接收信号多普勒频率和码相位估计的二维搜索过程；捕获过程可以看作一个二元假设检验问题，假设H0——信号不存在(只有干扰和噪声)；假设H1——信号存在。伪码捕获方法基于伪码良好的自相关特性，将接收信号混频后与本地伪码进行相关运算，通过检测检波器输出的相关峰与门限的关系来判断哪一假设成立，从而判定捕获是否成功[15]。

不考虑多普勒频率、伪码相位和衰落对捕获的影响，接收机收到的信号经下变频的数字基带信号可表示为：

式中：A为接收信号幅度；C(t)为伪码序列，是幅度为+1或-1的矩形波信号，伪码码长为L；τd为伪码时延；Ts为采样时间间隔；z(t)表示落入接收频带的PIM干扰信号与噪声的和。

接收信号经过数字解扩，即与本地伪码进行相关运算后，在时刻k的输出为：

(11)

考虑伪码的自相关特性，可以得到：

R的概率密度由zl的概率密度决定，落入接收频带的PIM干扰信号的概率密度由式(6)表示，接收机噪声的概率密度通常由均值为0的高斯分布N(0,σ2)表示，σ为标准差。因此，仅考虑单一阶次的PIM信号时，zl的概率密度为[14]：

其中，

zl相互独立且同分布，则H0情况下R的概率密度：

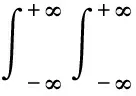
fZ(z-zL-1)dz1dz2…dzL-1

(18)

D(Z)=E(Z2)-E2(Z)=

E[(z1+z2+…+zL)2]-[LE(zl)]2=

(19)

则H1情况下的R可写作:

则H1情况下R的概率密度：

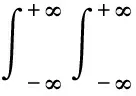
fZ(z-zL-1)dz1dz2…dzL-1

(21)

3 PIM对伪码捕获性能的影响

伪码捕获常采用平方律检波器和平方检波累积器捕获方法进行信号检测[16]，下面针对这两种方法分析检测概率和虚警概率。

3.1 平方律检波器的捕获方法

平方律检波器输出为：

则H0情况下的概率密度为：

根据中心极限定理，当L足够大时，R服从高斯分布，则RDT服从指数分布，其概率密度为：

H1情况下的概率密度为：

fDT(x/H1)=

当L足够大时，RDT服从自由度为2的非中心卡方分布，非中心参量λ0=A2L2，其概率密度为：

式中：I0(·)为零阶修正的贝塞尔函数。取门限为VT，则可以得到捕获信号的虚警概率为：

检测概率为：

3.2 平方检波累积器的捕获方法

平方检波累积器的输出为：

其实数码单反相机最初的设计理念就是将胶片单反相机“数码化”，那么所有感光元件与35mm胶片大小相同或几乎类似的机型就是全画幅机型。

平方检波累积器是在平方律检波器的基础上M项求和，因此在H0情况下的概率密度为：

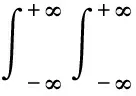
fDT(x2-x1/H0)…fDT(x-xM-1/H0)·

dx1dx2…dxM-1

(30)

当L足够大时，Rsum服从自由度为2M的Г分布[15]，其概率密度为：

(31)

H1情况下的概率密度为：

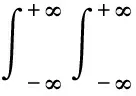
fDT(x2-x1/H1)…fDT(x-xM-1/H1)·

当L足够大时，Rsum服从自由度为2M的非中心卡方分布，非中心参量λ0=A2L2，其概率密度为：

(33)

式中：IM-1(·)为(M-1)阶修正的贝塞尔函数。取门限仍为VT，则可以得到捕获信号的虚警概率和检测概率分别为：

4 仿真结果分析

伪码捕获通常采用恒虚警检测方法设置检测门限，动态调整检测门限来保证虚警概率恒定。为方便门限设置，采用噪声干扰情况下的门限设置方法，即将干扰和噪声的功率乘以一个标度因子X0确定VT，平方律检波器的标度因子为X0≈-2lnffa。

定义干噪比(Interference to Noise Ratio,INR)为：

定义信干噪比(Signal to Interference plus Noise Ratio,SINR)为：

在设定虚警概率为10-3的条件下，采用平方律检波器捕获方法，仿真可以得到不同伪码长度L情况下检测概率随SINR变化的曲线，如图3所示，L分别取1，31和1 023，仿真采用9阶PIM干扰信号，INR=3 dB。由图3可以看出，各曲线之间区别不明显，当干扰过强时，增加系统的扩频增益无法实现对PIM干扰的抑制。在高SINR情况下，随着L的增大，检测概率降低。

不同INR下PIM干扰信号对捕获检测概率的影响如图4所示，仿真采用9阶PIM干扰信号，L=31。由图4可见，在高SINR情况下，随着INR的增大，检测概率提高。受相同功率的PIM干扰和噪声影响时，要达到90%的捕获检测概率，噪声干扰下的SINR需达到14.59 dB，而PIM干扰下的SINR仅需11.67 dB，二者相差2.92 dB。可见高SINR下，PIM干扰信号对捕获检测概率的影响比噪声的影响小一些;而低SINR下，PIM干扰信号对捕获概率的影响更大。

不同阶次PIM干扰信号对捕获检测概率的影响如图5所示，随着PIM阶次的增大，检测概率提高。可见高SINR下，低阶PIM干扰信号对捕获检测概率的影响更大，而低SINR下，高阶PIM干扰信号对捕获概率的影响大。

在设定虚警概率为10-3的条件下，采用平方检波累积器，仿真得到不同累积数目M情况下检测概率随SINR变化曲线，如图6所示，M分别取1，5和10。可以看出，在捕获检测概率为90%的条件下，采用平方律检波器时要求SINR达到13.53 dB，而采用10次累积的平方检波累积器仅要求SINR达11.17 dB，累积增益达2.36 dB。在高SINR情况下，采用平方检波累积器可以明显提高检测概率，随着累积数目M的增大，检测概率改善更加明显。

5 结束语

本文定量分析了PIM干扰对直接扩频通信系统捕获性能的影响，并给出了采用平方律检波器和采用平方检波累积器两种捕获方法下的检测概率闭式解，结果表明PIM干扰下的捕获检测概率在高SINR和低SINR条件下呈现不同特点。高SINR条件下，短扩频码、高阶PIM和大累积数可获得更高的捕获检测概率。

本文仅针对PIM干扰下的直扩系统伪码同步捕获性能进行了分析与仿真，尚未对同步环节中的跟踪性能进行分析；此外，本文所得结论还需通过实际测量做进一步验证。

本文研究内容丰富了PIM对通信性能影响的分析。研究成果可广泛用于采用扩频通信方式的通信系统，包括卫星导航系统、卫星测控系统及采用码分多址的移动通信基站等。一方面可用于PIM对扩频通信系统影响的综合分析；另一方面可用于指导扩频通信系统各组件PIM指标的制定。

References)

[1] 何鋆，李军，崔万照，等. 分布式无源互调研究综述[J]. 空间电子技术，2016，13(4)：1-6.

HE Y，LI J，CUI W Z，et al. Review of research on distributed passive intermodulation[J]. Space Electronic Technology，2016，13(4)：1-6(in Chinese).

[2] ZHAO P，ZHANG X P，YANG D C，et al. Superposition effect of passive intermodulation for cable assemblies with discrete point-sources[J]. China Communications，2015，12(4)：97-105.

[3] 李韵，崔万照，张洪太，等. 星载大功率复杂微波部件微放电效应数值模拟[J]. 中国空间科学技术，2017，37(2)：73-80.

LI Y，CUI W Z，ZHANG H T，et al. A novel simulation method of multipactor in complex component for satellite application[J]. Chinese Space Science and Technology，2017，37(2)：73-80(in Chinese).

[4] 陈翔，崔万照，李军，等. 空间大功率微波部件无源互调检测与定位技术[J]. 空间电子技术，2015，12(6)：1-7.

CHEN X，CUI W Z，LI J，et al. Measurement and localization of passive intermodulation distortion of high power microwave component for space application[J]. Space Electronic Technology，2015，12(6)：1-7(in Chinese).

[5] KOZLOV D S，SHITVOV A P，SHCUCHINSKY A G，et al. Passive intermodulation of analog and digital signals on transmission lines with distributed nonlinearities: modelling and characterization[J]. IEEE Transactions on Microwave Theory & Techniques，2016，64(5)：1-13.

[6] 方天琪，胡天存，田露，等. LDPC码对无源互调干扰下通信性能改善研究[J]. 中国空间科学技术，2017，37(2):108-113.

FANG T Q，HU T C，TIAN L，et al. Study on communication performance improvement using LDPC code under passive intermodulation interference[J]. Chinese Space Science and Technology，2017，37(2)：108-113(in Chinese).

[7] ENG K Y，YUE O C. High-order intermodulation effects in digital satellite channels[J]. IEEE Transactions on Aerospace & Electronic Systems，1981，AES-17(3)：438-445.

[8] 张世全，傅德民，葛德彪. 无源互调干扰对通信系统抗噪性能的影响[J]. 电波科学学报，2002，17(2)：138-142.

ZHANG S Q，FU D M，GE D B. The effects of passive intermodulation interference on the anti-noise property of communication systems[J]. Chinese Journal of Radio Science，2002，17(2)：138-142(in Chinese).

[9] Al-MUDHAFAR A，HARTNAGEL H. Bit error probability in the presence of passive intermodulation[J]. IEEE Communications Letters，2012，16(8)：1145-1148.

[10] 安金坤，田林，丁凯. 一种扩频测控链路中PIM的全盲抑制算法[J]. 中国空间科学技术，2016，36(4)：47-50.

AN J K，TIAN L，DING K. A full-blind PIM suppression algorithm for spread spectrum TT & C link[J]. Chinese Space Science and Technology，2016，36(4)：47-50(in Chinese).

[11] 胡天存，曹猛，鲍艳，等. 基于ZnO阵列的银表面二次电子发射抑制技术[J].中国空间科学技术，2017，37(2)：54-60.

HU T C，CAO M，BAO Y，et al. Technique for inhibiting secondary electron emission of silver based on ZnO array[J]. Chinese Space Science and Technology，2017，37(2)：54-60(in Chinese).

[12] 禹旭敏，唐小宏，汪娟，等. 大功率同轴谐振器连接缝隙EML和PIM研究[J]. 中国空间科学技术，2016，36(2):81-86.

YU X M，TANG X H，WANG J，et al. Study on EML and PIM from connection gap in a high power coaxial resonator[J]. Chinese Space Science and Technology，2016，36(2)：81-86(in Chinese).

[13] ZHAO P，ZHANG X P，YANG D C. Analysis of passive intermodulation generated by broadband signals[J]. Electronics Letters，2016，52(7)：564-566.

[14] TIAN L，WANG Y，WANG R F，et al. Modified Cauchy distribution model of high-order passive intermodulation[C]∥International Symposium on Antennas and Propagation. Okinawa：IEEE，2016：586-587.

[15] 苏悦，王建辉. GNSS弱信号两级快速傅里叶变换捕获方法[J]. 中国空间科学技术，2014，34(4)：66-71.

SU Y，WANG J H. Weak GNSS signals acquisition algorithm using two-stage FFT[J]. Chinese Space Science and Technology，2014，34(4)：66-71(in Chinese).

[16] 韩航程，刘井龙，梁丹丹，等. 基于FFT的高数据率低信噪比下的长码直捕算法[J]. 北京理工大学学报，2016，36(9)：976-982.

HANG H C，LIU J L，LIANG D D，et al. Long code direct acquisition algorithm of DSSS signals based on FFT in high rate and low SNR condition[J]. Transactions of Beijing Institute of Technology，2016，36(9)：976-982(in Chinese).