基于降维观测器的最优故障诊断算法研究

，,2,*，

1.北京控制工程研究所，北京 100190 2.北京空间飞行器总体设计部，北京 100094

近年来，面对航空航天等现代工业高可靠、长寿命的迫切需求，国内外关于故障诊断与重构技术的研究已经有了巨大发展[1-4]。凭借实时性高、对输入信号要求较低等优点，基于观测器的故障诊断算法得到了广泛应用。从观测器的设计原理来看，目前该类故障诊断算法主要有：未知输入观测器法(UIO)[5-6]、自适应观测器法[7-8]以及H2/H∞鲁棒观测器法[9]等。而从观测器的规模来看，该类故障诊断算法又可以分为：全维观测器法和降维观测器法。由于前者计算量大,响应速度慢，在系统较为复杂且实时性要求较高时，其实用性远不如后者。然而，后者通常需要进行矩阵分块运算，当系统规模较大时，该项工作十分繁琐，会影响诊断算法的响应速度[10]。因此，有必要研究无需进行矩阵分块运算的降维观测器故障诊断算法。

另一方面，在诊断器设计过程当中，非常关键的一步就是观测器增益的选取问题，现有文献多采用各类不等式进行求解[7-8]，由此来保证诊断结果的收敛性。然而，收敛并不代表诊断结果最优。文献[11-12]基于对偶原理，证明了某系统的(最优)观测器设计问题可以转换为对偶系统的(最优)控制器设计问题。在上述结论的指导下，可以进一步确定诊断算法的最优增益。

此外，实际工程应用当中，常常会遇到这样一种情况：虽然不知道真实的故障何时发生、发生时幅值为多大，但知道故障的类型，对其变化特性具有一定的认知。换言之，这类故障的动态特性是已知的，而具体发生时刻与初始状态未知，需进行诊断辨识得到。

因此，本文针对一类动态特性已知的快变偏差故障，利用正交原理和对偶原理，设计了一种无需进行矩阵分块运算且增益最优的基于降维观测器的故障诊断算法，实现了对故障的最小方差估计。在此基础之上，利用诊断结果对故障系统进行了控制重构。最后，通过数值仿真，验证了所提方法的有效性。

1 问题描述

假设m个执行器中有mk个受故障影响，考虑如下故障系统模型：

式中：x∈Rn、u∈Rm、y∈Rq分别为系统的状态向量、控制输入向量及输出向量；A、B、C为相应维度的常量矩阵；fa∈Rmk为执行机构的故障信号，不可直接测量，fai是fa的第i个分量；bi代表B的第i列，Fa是故障执行机构对应的编号集，F∈Rn×mk由故障执行机构编号对应的bi顺序组合而成，即F=[bi],i∈Fa。

这里借鉴文献[13-14]中的故障模型描述方法，利用一个“外系统”来描述动态特性已知的故障fa，具体表示如下：

式中：xfa∈Rr是执行机构故障的状态向量。Afa和Cfa是适当维数的常量矩阵。故障的发生时刻tf和初始状态xfa0是未知的。

上述故障描述方法可用于正弦曲线型故障、斜坡型故障、阶跃型故障、发散型故障、收敛型故障以及其他更一般的持续型故障，具有广泛的适用性。

2 故障诊断与重构

2.1 故障诊断

下面设计一种基于降维扩展状态观测器的故障诊断算法。

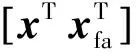
(3)

令W11∈Rn×q,W21∈Rr×q,W12∈Rn×(n+r-q)，W22∈Rr×(n+r-q)，构造如下降阶观测器，即故障诊断器：

设观测误差为：

代入式(4)和式(5)，可得观测误差方程为：

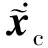
文献[11-12]基于对偶原理，论证了(最优)观测器的设计问题可以转换为对偶系统的(最优)控制器设计问题。

式(7)误差方程的对偶系统为：

设：

它可以视为对偶系统的等效控制输入，其中LT为等效状态反馈增益，则式(8)闭环系统等价于：

文献[12]证明了待观测状态的线性加权Txc(t)的估计方差可转化成如下形式的积分二次型函数：

J=ψT(t0)S0ψ(t0)+

式中：S0,S∈R(n+r-q)×(n+r-q)和R∈Rq×q分别是正定和半正定矩阵。

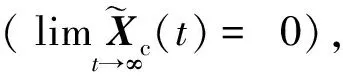
(12)

由最优控制理论，可以求得式(10)系统在式(12)二次性能指标下的最优控制律为：

式中：H是下列Riccati矩阵方程的唯一正定解：

对比式(13)和式(9)，可得最优故障诊断器的状态反馈增益矩阵L为：

2.2 控制重构

基于上述故障诊断结果，可以设计重构控制器，以实现系统与故障的隔离。

假设标称模型的控制目标是：在规定任务时间tmis内，使系统跟踪到期望模型：

在已经诊断出故障的前提下，设计相应的容错控制律ur(t)以隔离故障。可采用故障补偿的思想，在标称控制律un(t)的基础之上附加故障补偿项uξ(t)，即：

这里不妨采用状态反馈控制器作为标称控制器，即un(t)=-Kx(t)。其中，反馈增益K满足：

以一般的伪逆法为例，反馈增益K可取为：

由于F=[bi],i∈Fa，所以存在一个矩阵Ma，使得F=BMa，因此uξ(t)可以设计为：

通过上述故障诊断器和重构控制器的构建，实现了故障系统的主动容错控制。

3 数值仿真验证

为了验证上述诊断算法的有效性，这里采用文献[15]的算例，进行数值仿真验证。

考虑式(1)描述的含加性时变故障的线性定常系统，其中的矩阵参数及初始状态如下：

式(2)描述的故障模型参数矩阵如下：

式(16)所示期望模型的系统矩阵为：

取故障发生时刻为：tf=25 s。

预定任务完成时间为：tmis=100 s。

根据(15)求得故障诊断器的增益矩阵L为：

在以上的参数条件下，仿真结果如图1～图7所示。

由图1、图2可知，系统在25 s时发生周期性时变故障，故障后系统输出周期性振荡，不再收敛为零。

通过对系统输入输出的测量，最优故障诊断器得到的故障诊断值和真实值如图3所示，诊断误差如图4所示，可见该故障诊断器可在7 s内快速收敛到真实值，由此验证了诊断器的有效性。

假设系统发生故障后立即进行控制重构，即tr=tf=25 s，得到重构后的系统响应曲线如图5所示，可见系统输出在重构控制器的作用下能够重新收敛于期望值，由此验证了重构控制器的有效性。

图6、图7为分别在tr1=25 s、tr2=31 s进行控制器重构的系统输入输出响应曲线。结果显示：虽然尽早地采取重构措施，会降低系统偏差，但需要以更大的控制输入为代价，因此重构时刻并非越快越好，需要折衷考虑状态偏差与重构代价等多重因素。

4 结束语

本文利用正交原理和对偶原理，设计了一种基于降维观测器的最优故障诊断算法，在此基础之上实现了对故障系统的控制重构。该算法具有如下优点：

1)无需进行矩阵分块运算即可对诊断器进行降维，降低了计算的复杂性；

2)通过求解对偶系统的最优控制律，即可确定诊断算法的最优增益，从而实现对故障的最小方差估计。

最后，通过数值仿真，得到以下结论：

1)本文所提最优降维故障诊断算法能够快速有效地估计出系统故障，给出故障初值与发生时刻；

2)对系统进行控制重构并非越早越好，因为尽早重构虽然会降低系统偏差，但需要以更大的控制输入为代价。

References)

[1] 顾朋, 王大轶, 刘成瑞.零动量轮卫星控制系统可重构性设计研究[J]. 中国空间科学技术, 2013,33(1): 7-14.

GU P， WANG D Y, LIU C R. Research on momentum wheel reconfiguration design of zero-momentum satellite[J]. Chinese Space Science and Technology, 2013,33(1): 7-14(in Chinese).

[2] 胡宇桑, 王大轶, 刘成瑞. 基于能耗与可靠性约束的动量轮可重构性评价[J]. 中国空间科学技术, 2014, 34(5): 10-17.

HU Y S, WANG D Y, LIU C R. Reconfigurability evaluation of momentum wheel control system under energy and reliability constraints[J]. Chinese Space Science and Technology, 2014, 34(5):10-17(in Chinese).

[3] 李文博，王大轶，刘成瑞. 动态系统实际故障可诊断性的量化评价研究[J]. 自动化学报, 2014, 41(3):497-507.

LI W B, WANG D Y, LIU C R. Quantitative evaluation of actual fault diagnosability for dynamic systems[J]. Acta Automatica Sinica, 2014, 41(3):497-507(in Chinese).

[4] YIN S, XIAO B, DING S X, et al. A review on recent development of spacecraft attitude fault tolerant control system[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3311-3320.

[5] HAMDAOUI R, ABDELKRIM M N. Timely actuator fault diagnosis and accommodation[C]∥International Multi-conference on System, Signals & Devices. Hammamet: IEEE, 2013: 1-8.

[6] HAMDAOUI R, GUESMI S, EI HARABI R. UIO based robust fault detection and estimation[C]∥Proceedings of International Conference on Control.Strbske Pleso, Slovakia,2013: 076-081.

[7] ZHANG K, JIANG B, COCQUEMPOT V. Adaptive observer-based fast fault estimation[J]. International Journal of Control Automation & Systems, 2008, 6(3): 320-326.

[8] JIANG B, STAROSWIECKI M. Adaptive observer design for robust fault estimation[J]. International Journal of Systems Science, 2010, 33(33): 767-775.

[9] COLLINS E G, SONG T. ROBUST H∞ estimation and fault detection of uncertain dynamic systems[J]. Journal of Guidance Control & Dynamics, 2000, 23(5): 857-864.

[10] TANG G Y, LI J. Optimal fault diagnosis for systems with delayed measurements[J]．IET Control Theory & Applications, 2008, 2(11): 990-998.

[11] 韩京清. 线性控制系统的对偶性[J]. 数学年刊:中文版, 1980(1): 31-39.

[12] 言茂松. 最佳控制与观测(五)[J]. 电气传动, 1979(3): 53-70.

[13] JOSHI S M, GONZLEZ O R, UPCHURCH J M. Identifiability of additive, time-varying actuator and sensor faults by state augmentation,NASA/TM-2014-218669[R].Washington DC:NASA, 2014.

[14] JOSHI SM, GONZLEZ O R, UPCHURCH J M. Identifiability of additive actuator and sensor faults by state augmentation[J]. Journal of Guidance Control & Dynamics,2014, 37(3): 941-946.

[15] TANG G Y, LI J. Optimal fault diagnosis for systems with delayed measurements[J]. Iet Control Theory & Applications, 2008, 2(11): 990-998.